Minimax-Bayes Reinforcement Learning

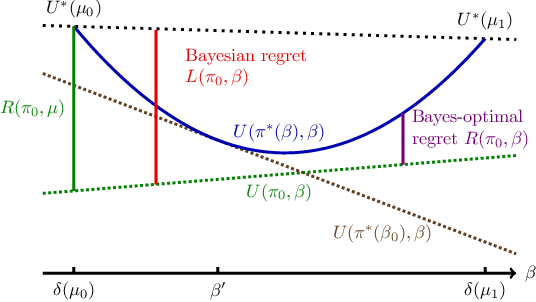
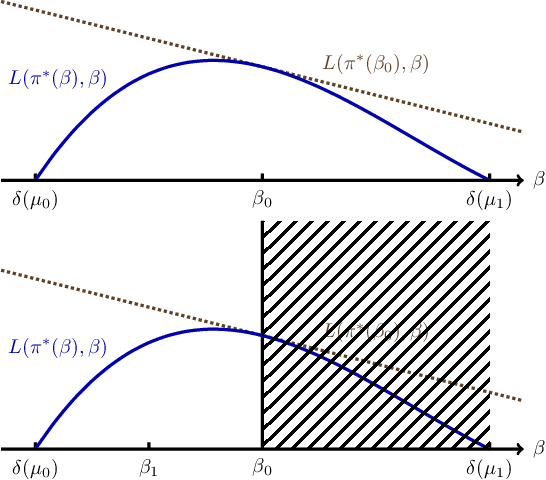
While the Bayesian decision-theoretic framework offers an elegant solution to the problem of decision making under uncertainty, one question is how to appropriately select the prior distribution. One idea is to employ a worst-case prior. However, this is not as easy to specify in sequential decision making as in simple statistical estimation problems. This paper studies (sometimes approximate) minimax-Bayes solutions for various reinforcement learning problems to gain insights into the properties of the corresponding priors and policies. We find that while the worst-case prior depends on the setting, the corresponding minimax policies are more robust than those that assume a standard (i.e. uniform) prior.

Reinforcement Learning in the Wild with Maximum Likelihood-based Model Transfer

In this paper, we study the problem of transferring the available Markov Decision Process (MDP) models to learn and plan efficiently in an unknown but similar MDP. We refer to it as \textit{Model Transfer Reinforcement Learning (MTRL)} problem. First, we formulate MTRL for discrete MDPs and Linear Quadratic Regulators (LQRs) with continuous state actions. Then, we propose a generic two-stage algorithm, MLEMTRL, to address the MTRL problem in discrete and continuous settings. In the first stage, MLEMTRL uses a \textit{constrained Maximum Likelihood Estimation (MLE)}-based approach to estimate the target MDP model using a set of known MDP models. In the second stage, using the estimated target MDP model, MLEMTRL deploys a model-based planning algorithm appropriate for the MDP class. Theoretically, we prove worst-case regret bounds for MLEMTRL both in realisable and non-realisable settings. We empirically demonstrate that MLEMTRL allows faster learning in new MDPs than learning from scratch and achieves near-optimal performance depending on the similarity of the available MDPs and the target MDP.

Risk-Sensitive Bayesian Games for Multi-Agent Reinforcement Learning under Policy Uncertainty

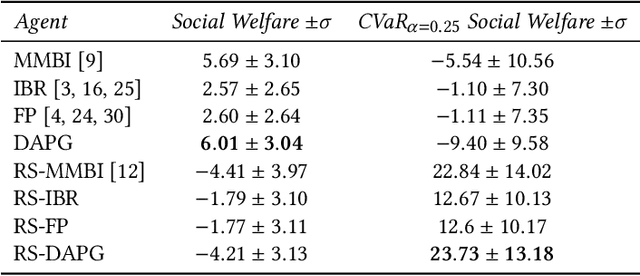
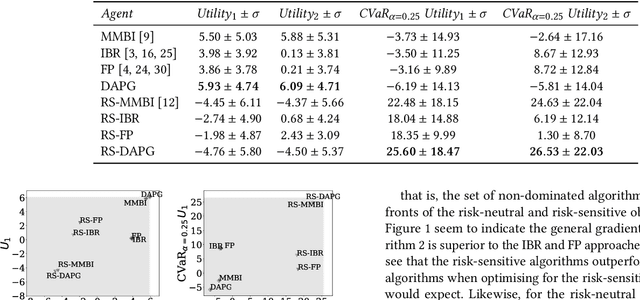
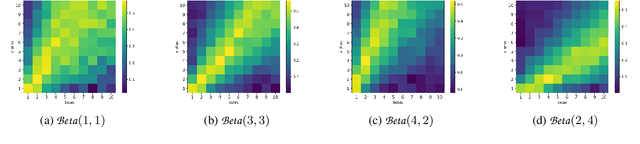
In stochastic games with incomplete information, the uncertainty is evoked by the lack of knowledge about a player's own and the other players' types, i.e. the utility function and the policy space, and also the inherent stochasticity of different players' interactions. In existing literature, the risk in stochastic games has been studied in terms of the inherent uncertainty evoked by the variability of transitions and actions. In this work, we instead focus on the risk associated with the \textit{uncertainty over types}. We contrast this with the multi-agent reinforcement learning framework where the other agents have fixed stationary policies and investigate risk-sensitiveness due to the uncertainty about the other agents' adaptive policies. We propose risk-sensitive versions of existing algorithms proposed for risk-neutral stochastic games, such as Iterated Best Response (IBR), Fictitious Play (FP) and a general multi-objective gradient approach using dual ascent (DAPG). Our experimental analysis shows that risk-sensitive DAPG performs better than competing algorithms for both social welfare and general-sum stochastic games.

High-dimensional near-optimal experiment design for drug discovery via Bayesian sparse sampling

We study the problem of performing automated experiment design for drug screening through Bayesian inference and optimisation. In particular, we compare and contrast the behaviour of linear-Gaussian models and Gaussian processes, when used in conjunction with upper confidence bound algorithms, Thompson sampling, or bounded horizon tree search. We show that non-myopic sophisticated exploration techniques using sparse tree search have a distinct advantage over methods such as Thompson sampling or upper confidence bounds in this setting. We demonstrate the significant superiority of the approach over existing and synthetic datasets of drug toxicity.

SENTINEL: Taming Uncertainty with Ensemble-based Distributional Reinforcement Learning

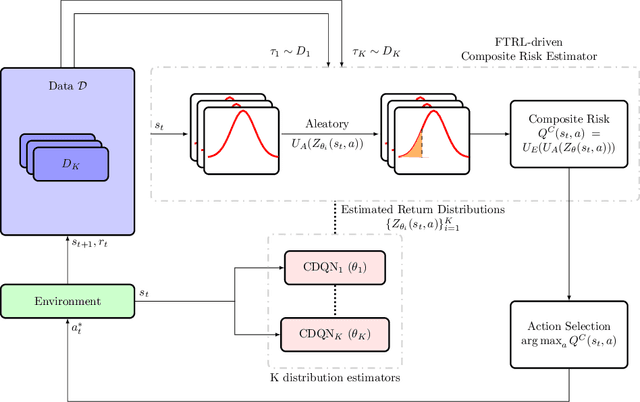
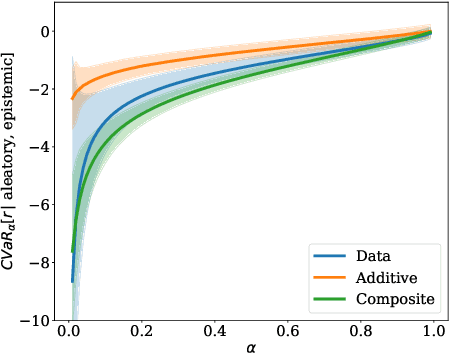
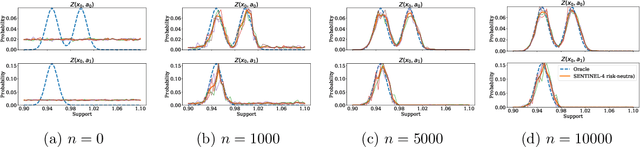
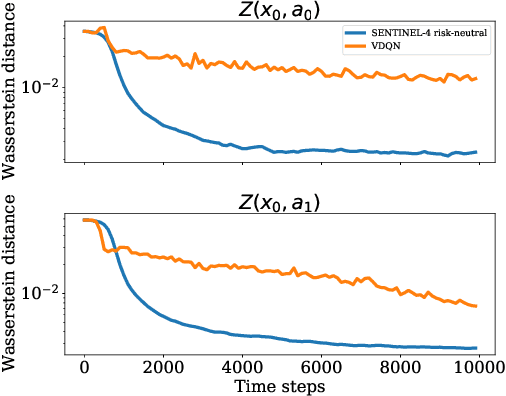
In this paper, we consider risk-sensitive sequential decision-making in model-based reinforcement learning (RL). We introduce a novel quantification of risk, namely \emph{composite risk}, which takes into account both aleatory and epistemic risk during the learning process. Previous works have considered aleatory or epistemic risk individually, or, an additive combination of the two. We demonstrate that the additive formulation is a particular case of the composite risk, which underestimates the actual CVaR risk even while learning a mixture of Gaussians. In contrast, the composite risk provides a more accurate estimate. We propose to use a bootstrapping method, SENTINEL-K, for distributional RL. SENTINEL-K uses an ensemble of $K$ learners to estimate the return distribution and additionally uses follow the regularized leader (FTRL) from bandit literature for providing a better estimate of the risk on the return distribution. Finally, we experimentally verify that SENTINEL-K estimates the return distribution better, and while used with composite risk estimate, demonstrates better risk-sensitive performance than competing RL algorithms.

Inferential Induction: Joint Bayesian Estimation of MDPs and Value Functions

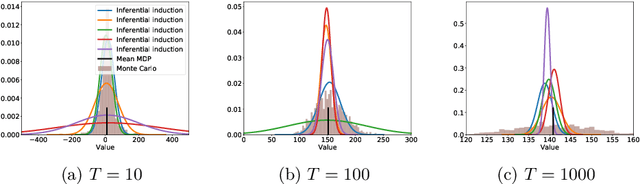
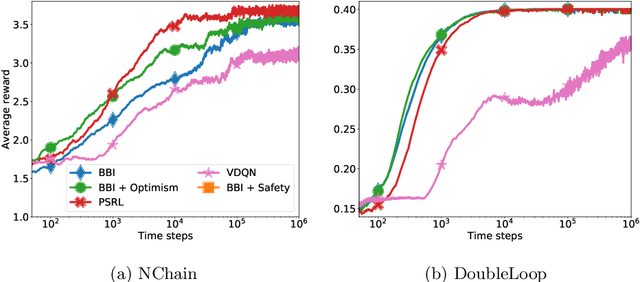
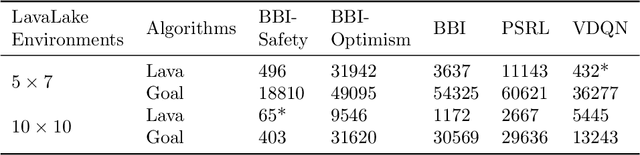
Bayesian reinforcement learning (BRL) offers a decision-theoretic solution to the problem of reinforcement learning. However, typical model-based BRL algorithms have focused either on ma intaining a posterior distribution on models or value functions and combining this with approx imate dynamic programming or tree search. This paper describes a novel backwards induction pri nciple for performing joint Bayesian estimation of models and value functions, from which many new BRL algorithms can be obtained. We demonstrate this idea with algorithms and experiments in discrete state spaces.

Epistemic Risk-Sensitive Reinforcement Learning

We develop a framework for interacting with uncertain environments in reinforcement learning (RL) by leveraging preferences in the form of utility functions. We claim that there is value in considering different risk measures during learning. In this framework, the preference for risk can be tuned by variation of the parameter $\beta$ and the resulting behavior can be risk-averse, risk-neutral or risk-taking depending on the parameter choice. We evaluate our framework for learning problems with model uncertainty. We measure and control for \emph{epistemic} risk using dynamic programming (DP) and policy gradient-based algorithms. The risk-averse behavior is then compared with the behavior of the optimal risk-neutral policy in environments with epistemic risk.