SENTINEL: Taming Uncertainty with Ensemble-based Distributional Reinforcement Learning

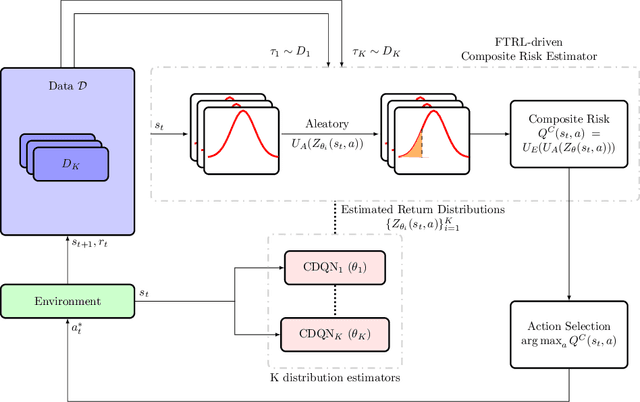
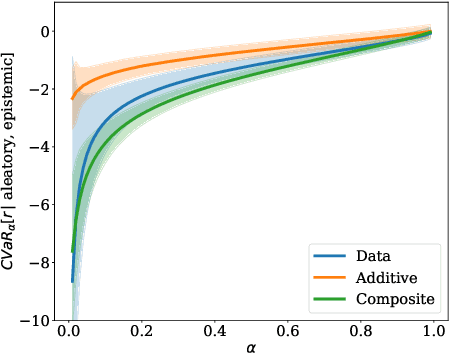
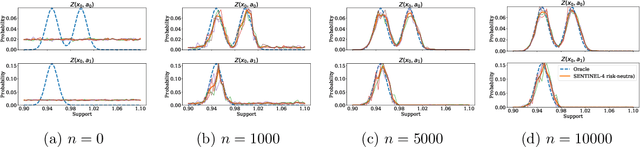
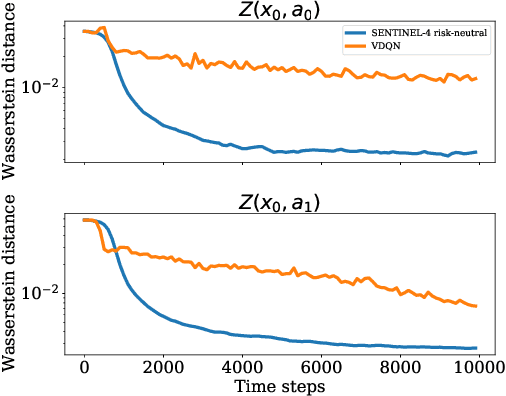
In this paper, we consider risk-sensitive sequential decision-making in model-based reinforcement learning (RL). We introduce a novel quantification of risk, namely \emph{composite risk}, which takes into account both aleatory and epistemic risk during the learning process. Previous works have considered aleatory or epistemic risk individually, or, an additive combination of the two. We demonstrate that the additive formulation is a particular case of the composite risk, which underestimates the actual CVaR risk even while learning a mixture of Gaussians. In contrast, the composite risk provides a more accurate estimate. We propose to use a bootstrapping method, SENTINEL-K, for distributional RL. SENTINEL-K uses an ensemble of $K$ learners to estimate the return distribution and additionally uses follow the regularized leader (FTRL) from bandit literature for providing a better estimate of the risk on the return distribution. Finally, we experimentally verify that SENTINEL-K estimates the return distribution better, and while used with composite risk estimate, demonstrates better risk-sensitive performance than competing RL algorithms.