Two-Player Zero-Sum Games with Bandit Feedback

We study a two-player zero-sum game (TPZSG) in which the row player aims to maximize their payoff against an adversarial column player, under an unknown payoff matrix estimated through bandit feedback. We propose and analyze two algorithms: ETC-TPZSG, which directly applies ETC to the TPZSG setting and ETC-TPZSG-AE, which improves upon it by incorporating an action pair elimination (AE) strategy that leverages the $\varepsilon$-Nash Equilibrium property to efficiently select the optimal action pair. Our objective is to demonstrate the applicability of ETC in a TPZSG setting by focusing on learning pure strategy Nash Equilibrium. A key contribution of our work is a derivation of instance-dependent upper bounds on the expected regret for both algorithms, has received limited attention in the literature on zero-sum games. Particularly, after $T$ rounds, we achieve an instance-dependent regret upper bounds of $O(\Delta + \sqrt{T})$ for ETC-TPZSG and $O(\frac{\log (T \Delta^2)}{\Delta})$ for ETC-TPZSG-AE, where $\Delta$ denotes the suboptimality gap. Therefore, our results indicate that ETC-based algorithms perform effectively in adversarial game settings, achieving regret bounds comparable to existing methods while providing insights through instance-dependent analysis.

Learning Equilibria in Matching Games with Bandit Feedback

We investigate the problem of learning an equilibrium in a generalized two-sided matching market, where agents can adaptively choose their actions based on their assigned matches. Specifically, we consider a setting in which matched agents engage in a zero-sum game with initially unknown payoff matrices, and we explore whether a centralized procedure can learn an equilibrium from bandit feedback. We adopt the solution concept of matching equilibrium, where a pair consisting of a matching $\mathfrak{m}$ and a set of agent strategies $X$ forms an equilibrium if no agent has the incentive to deviate from $(\mathfrak{m}, X)$. To measure the deviation of a given pair $(\mathfrak{m}, X)$ from the equilibrium pair $(\mathfrak{m}^\star, X^\star)$, we introduce matching instability that can serve as a regret measure for the corresponding learning problem. We then propose a UCB algorithm in which agents form preferences and select actions based on optimistic estimates of the game payoffs, and prove that it achieves sublinear, instance-independent regret over a time horizon $T$.

A Minimax Approach to Ad Hoc Teamwork

We propose a minimax-Bayes approach to Ad Hoc Teamwork (AHT) that optimizes policies against an adversarial prior over partners, explicitly accounting for uncertainty about partners at time of deployment. Unlike existing methods that assume a specific distribution over partners, our approach improves worst-case performance guarantees. Extensive experiments, including evaluations on coordinated cooking tasks from the Melting Pot suite, show our method's superior robustness compared to self-play, fictitious play, and best response learning. Our work highlights the importance of selecting an appropriate training distribution over teammates to achieve robustness in AHT.

Probably Correct Optimal Stable Matching for Two-Sided Markets Under Uncertainty

We consider a learning problem for the stable marriage model under unknown preferences for the left side of the market. We focus on the centralized case, where at each time step, an online platform matches the agents, and obtains a noisy evaluation reflecting their preferences. Our aim is to quickly identify the stable matching that is left-side optimal, rendering this a pure exploration problem with bandit feedback. We specifically aim to find Probably Correct Optimal Stable Matchings and present several bandit algorithms to do so. Our findings provide a foundational understanding of how to efficiently gather and utilize preference information to identify the optimal stable matching in two-sided markets under uncertainty. An experimental analysis on synthetic data complements theoretical results on sample complexities for the proposed methods.

Isoperimetry is All We Need: Langevin Posterior Sampling for RL with Sublinear Regret

In Reinforcement Learning (RL) theory, we impose restrictive assumptions to design an algorithm with provably sublinear regret. Common assumptions, like linear or RKHS models, and Gaussian or log-concave posteriors over the models, do not explain practical success of RL across a wider range of distributions and models. Thus, we study how to design RL algorithms with sublinear regret for isoperimetric distributions, specifically the ones satisfying the Log-Sobolev Inequality (LSI). LSI distributions include the standard setups of RL and others, such as many non-log-concave and perturbed distributions. First, we show that the Posterior Sampling-based RL (PSRL) yields sublinear regret if the data distributions satisfy LSI under some mild additional assumptions. Also, when we cannot compute or sample from an exact posterior, we propose a Langevin sampling-based algorithm design: LaPSRL. We show that LaPSRL achieves order optimal regret and subquadratic complexity per episode. Finally, we deploy LaPSRL with a Langevin sampler -- SARAH-LD, and test it for different bandit and MDP environments. Experimental results validate the generality of LaPSRL across environments and its competitive performance with respect to the baselines.

Strategic Linear Contextual Bandits

Motivated by the phenomenon of strategic agents gaming a recommender system to maximize the number of times they are recommended to users, we study a strategic variant of the linear contextual bandit problem, where the arms can strategically misreport their privately observed contexts to the learner. We treat the algorithm design problem as one of mechanism design under uncertainty and propose the Optimistic Grim Trigger Mechanism (OptGTM) that incentivizes the agents (i.e., arms) to report their contexts truthfully while simultaneously minimizing regret. We also show that failing to account for the strategic nature of the agents results in linear regret. However, a trade-off between mechanism design and regret minimization appears to be unavoidable. More broadly, this work aims to provide insight into the intersection of online learning and mechanism design.

Eliciting Kemeny Rankings

We formulate the problem of eliciting agents' preferences with the goal of finding a Kemeny ranking as a Dueling Bandits problem. Here the bandits' arms correspond to alternatives that need to be ranked and the feedback corresponds to a pairwise comparison between alternatives by a randomly sampled agent. We consider both sampling with and without replacement, i.e., the possibility to ask the same agent about some comparison multiple times or not. We find approximation bounds for Kemeny rankings dependant on confidence intervals over estimated winning probabilities of arms. Based on these we state algorithms to find Probably Approximately Correct (PAC) solutions and elaborate on their sample complexity for sampling with or without replacement. Furthermore, if all agents' preferences are strict rankings over the alternatives, we provide means to prune confidence intervals and thereby guide a more efficient elicitation. We formulate several adaptive sampling methods that use look-aheads to estimate how much confidence intervals (and thus approximation guarantees) might be tightened. All described methods are compared on synthetic data.

Bandits Meet Mechanism Design to Combat Clickbait in Online Recommendation

We study a strategic variant of the multi-armed bandit problem, which we coin the strategic click-bandit. This model is motivated by applications in online recommendation where the choice of recommended items depends on both the click-through rates and the post-click rewards. Like in classical bandits, rewards follow a fixed unknown distribution. However, we assume that the click-rate of each arm is chosen strategically by the arm (e.g., a host on Airbnb) in order to maximize the number of times it gets clicked. The algorithm designer does not know the post-click rewards nor the arms' actions (i.e., strategically chosen click-rates) in advance, and must learn both values over time. To solve this problem, we design an incentive-aware learning algorithm, UCB-S, which achieves two goals simultaneously: (a) incentivizing desirable arm behavior under uncertainty; (b) minimizing regret by learning unknown parameters. We characterize all approximate Nash equilibria among arms under UCB-S and show a $\tilde{\mathcal{O}} (\sqrt{KT})$ regret bound uniformly in every equilibrium. We also show that incentive-unaware algorithms generally fail to achieve low regret in the strategic click-bandit. Finally, we support our theoretical results by simulations of strategic arm behavior which confirm the effectiveness and robustness of our proposed incentive design.

Minimax-Bayes Reinforcement Learning

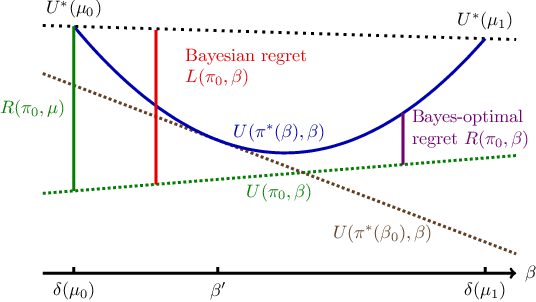
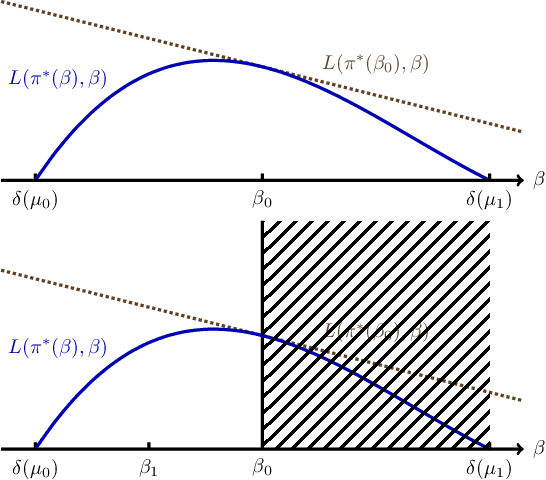
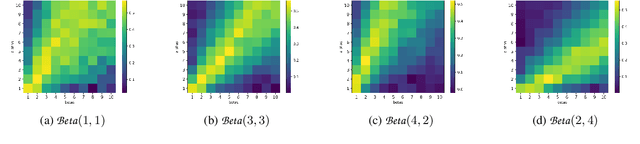
While the Bayesian decision-theoretic framework offers an elegant solution to the problem of decision making under uncertainty, one question is how to appropriately select the prior distribution. One idea is to employ a worst-case prior. However, this is not as easy to specify in sequential decision making as in simple statistical estimation problems. This paper studies (sometimes approximate) minimax-Bayes solutions for various reinforcement learning problems to gain insights into the properties of the corresponding priors and policies. We find that while the worst-case prior depends on the setting, the corresponding minimax policies are more robust than those that assume a standard (i.e. uniform) prior.

Reinforcement Learning in the Wild with Maximum Likelihood-based Model Transfer

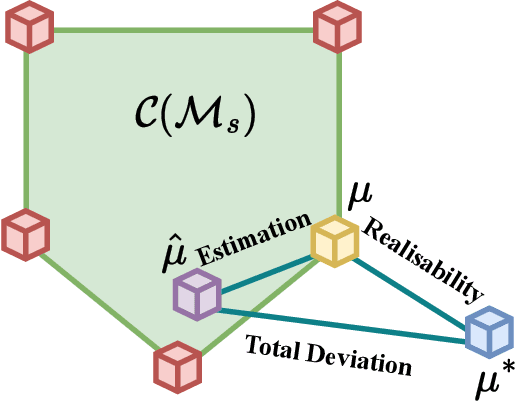
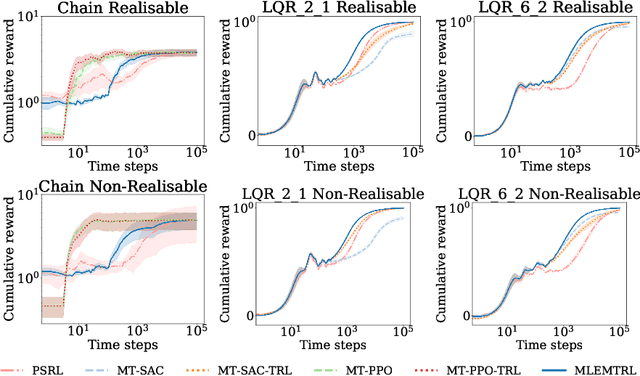
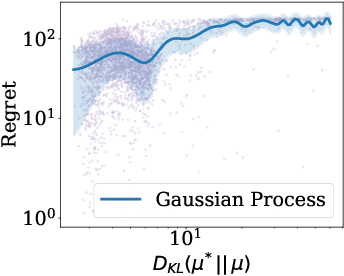
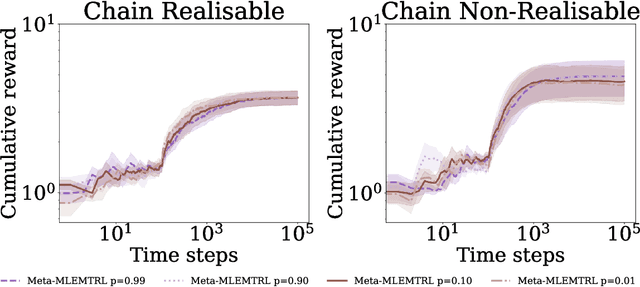
In this paper, we study the problem of transferring the available Markov Decision Process (MDP) models to learn and plan efficiently in an unknown but similar MDP. We refer to it as \textit{Model Transfer Reinforcement Learning (MTRL)} problem. First, we formulate MTRL for discrete MDPs and Linear Quadratic Regulators (LQRs) with continuous state actions. Then, we propose a generic two-stage algorithm, MLEMTRL, to address the MTRL problem in discrete and continuous settings. In the first stage, MLEMTRL uses a \textit{constrained Maximum Likelihood Estimation (MLE)}-based approach to estimate the target MDP model using a set of known MDP models. In the second stage, using the estimated target MDP model, MLEMTRL deploys a model-based planning algorithm appropriate for the MDP class. Theoretically, we prove worst-case regret bounds for MLEMTRL both in realisable and non-realisable settings. We empirically demonstrate that MLEMTRL allows faster learning in new MDPs than learning from scratch and achieves near-optimal performance depending on the similarity of the available MDPs and the target MDP.