Towards Fast Algorithms for the Preference Consistency Problem Based on Hierarchical Models

In this paper, we construct and compare algorithmic approaches to solve the Preference Consistency Problem for preference statements based on hierarchical models. Instances of this problem contain a set of preference statements that are direct comparisons (strict and non-strict) between some alternatives, and a set of evaluation functions by which all alternatives can be rated. An instance is consistent based on hierarchical preference models, if there exists an hierarchical model on the evaluation functions that induces an order relation on the alternatives by which all relations given by the preference statements are satisfied. Deciding if an instance is consistent is known to be NP-complete for hierarchical models. We develop three approaches to solve this decision problem. The first involves a Mixed Integer Linear Programming (MILP) formulation, the other two are recursive algorithms that are based on properties of the problem by which the search space can be pruned. Our experiments on synthetic data show that the recursive algorithms are faster than solving the MILP formulation and that the ratio between the running times increases extremely quickly.

Efficient Inference and Computation of Optimal Alternatives for Preference Languages Based On Lexicographic Models

We analyse preference inference, through consistency, for general preference languages based on lexicographic models. We identify a property, which we call strong compositionality, that applies for many natural kinds of preference statement, and that allows a greedy algorithm for determining consistency of a set of preference statements. We also consider different natural definitions of optimality, and their relations to each other, for general preference languages based on lexicographic models. Based on our framework, we show that testing consistency, and thus inference, is polynomial for a specific preference language LpqT, which allows strict and non-strict statements, comparisons between outcomes and between partial tuples, both ceteris paribus and strong statements, and their combination. Computing different kinds of optimal sets is also shown to be polynomial; this is backed up by our experimental results.

Eliciting Kemeny Rankings

We formulate the problem of eliciting agents' preferences with the goal of finding a Kemeny ranking as a Dueling Bandits problem. Here the bandits' arms correspond to alternatives that need to be ranked and the feedback corresponds to a pairwise comparison between alternatives by a randomly sampled agent. We consider both sampling with and without replacement, i.e., the possibility to ask the same agent about some comparison multiple times or not. We find approximation bounds for Kemeny rankings dependant on confidence intervals over estimated winning probabilities of arms. Based on these we state algorithms to find Probably Approximately Correct (PAC) solutions and elaborate on their sample complexity for sampling with or without replacement. Furthermore, if all agents' preferences are strict rankings over the alternatives, we provide means to prune confidence intervals and thereby guide a more efficient elicitation. We formulate several adaptive sampling methods that use look-aheads to estimate how much confidence intervals (and thus approximation guarantees) might be tightened. All described methods are compared on synthetic data.

Minimal Macro-Based Rewritings of Formal Languages: Theory and Applications in Ontology Engineering (and beyond)

In this paper, we introduce the problem of rewriting finite formal languages using syntactic macros such that the rewriting is minimal in size. We present polynomial-time algorithms to solve variants of this problem and show their correctness. To demonstrate the practical relevance of the proposed problems and the feasibility and effectiveness of our algorithms in practice, we apply these to biomedical ontologies authored in OWL. We find that such rewritings can significantly reduce the size of ontologies by capturing repeated expressions with macros. In addition to offering valuable assistance in enhancing ontology quality and comprehension, the presented approach introduces a systematic way of analysing and evaluating features of rewriting systems (including syntactic macros, templates, or other forms of rewriting rules) in terms of their influence on computational problems.

Interactive Inverse Reinforcement Learning for Cooperative Games

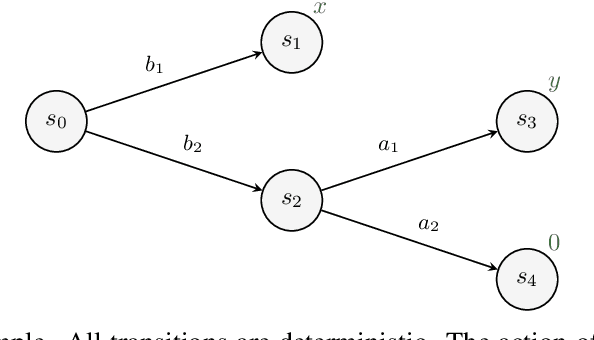
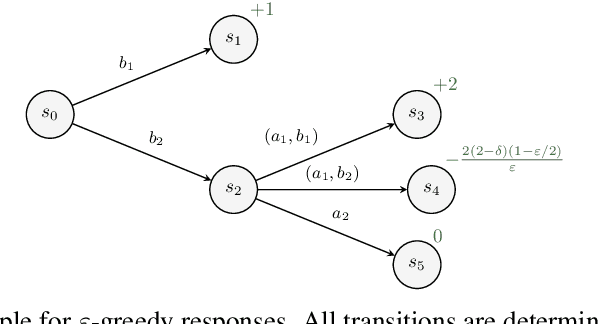
We study the problem of designing AI agents that can learn to cooperate effectively with a potentially suboptimal partner while having no access to the joint reward function. This problem is modeled as a cooperative episodic two-agent Markov decision process. We assume control over only the first of the two agents in a Stackelberg formulation of the game, where the second agent is acting so as to maximise expected utility given the first agent's policy. How should the first agent act in order to learn the joint reward function as quickly as possible, and so that the joint policy is as close to optimal as possible? In this paper, we analyse how knowledge about the reward function can be gained in this interactive two-agent scenario. We show that when the learning agent's policies have a significant effect on the transition function, the reward function can be learned efficiently.