Efficient Inference and Computation of Optimal Alternatives for Preference Languages Based On Lexicographic Models

We analyse preference inference, through consistency, for general preference languages based on lexicographic models. We identify a property, which we call strong compositionality, that applies for many natural kinds of preference statement, and that allows a greedy algorithm for determining consistency of a set of preference statements. We also consider different natural definitions of optimality, and their relations to each other, for general preference languages based on lexicographic models. Based on our framework, we show that testing consistency, and thus inference, is polynomial for a specific preference language LpqT, which allows strict and non-strict statements, comparisons between outcomes and between partial tuples, both ceteris paribus and strong statements, and their combination. Computing different kinds of optimal sets is also shown to be polynomial; this is backed up by our experimental results.

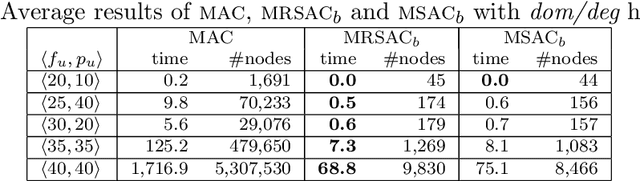
Towards Fast Algorithms for the Preference Consistency Problem Based on Hierarchical Models

In this paper, we construct and compare algorithmic approaches to solve the Preference Consistency Problem for preference statements based on hierarchical models. Instances of this problem contain a set of preference statements that are direct comparisons (strict and non-strict) between some alternatives, and a set of evaluation functions by which all alternatives can be rated. An instance is consistent based on hierarchical preference models, if there exists an hierarchical model on the evaluation functions that induces an order relation on the alternatives by which all relations given by the preference statements are satisfied. Deciding if an instance is consistent is known to be NP-complete for hierarchical models. We develop three approaches to solve this decision problem. The first involves a Mixed Integer Linear Programming (MILP) formulation, the other two are recursive algorithms that are based on properties of the problem by which the search space can be pruned. Our experiments on synthetic data show that the recursive algorithms are faster than solving the MILP formulation and that the ratio between the running times increases extremely quickly.

Quality of Geographic Information: Ontological approach and Artificial Intelligence Tools

The objective is to present one important aspect of the European IST-FET project "REV!GIS"1: the methodology which has been developed for the translation (interpretation) of the quality of the data into a "fitness for use" information, that we can confront to the user needs in its application. This methodology is based upon the notion of "ontologies" as a conceptual framework able to capture the explicit and implicit knowledge involved in the application. We do not address the general problem of formalizing such ontologies, instead, we rather try to illustrate this with three applications which are particular cases of the more general "data fusion" problem. In each application, we show how to deploy our methodology, by comparing several possible solutions, and we try to enlighten where are the quality issues, and what kind of solution to privilege, even at the expense of a highly complex computational approach. The expectation of the REV!GIS project is that computationally tractable solutions will be available among the next generation AI tools.

Developing Approaches for Solving a Telecommunications Feature Subscription Problem

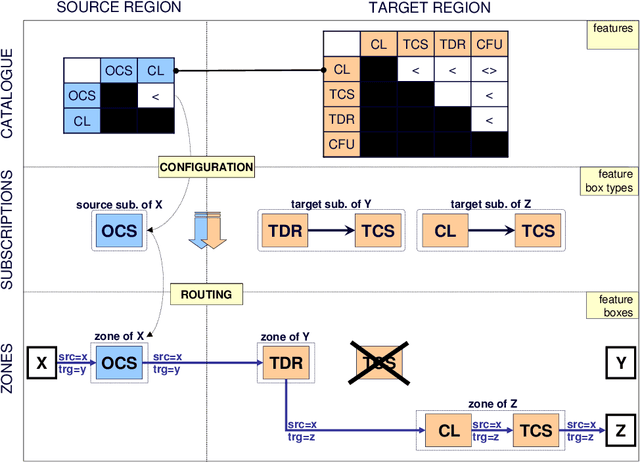
Call control features (e.g., call-divert, voice-mail) are primitive options to which users can subscribe off-line to personalise their service. The configuration of a feature subscription involves choosing and sequencing features from a catalogue and is subject to constraints that prevent undesirable feature interactions at run-time. When the subscription requested by a user is inconsistent, one problem is to find an optimal relaxation, which is a generalisation of the feedback vertex set problem on directed graphs, and thus it is an NP-hard task. We present several constraint programming formulations of the problem. We also present formulations using partial weighted maximum Boolean satisfiability and mixed integer linear programming. We study all these formulations by experimentally comparing them on a variety of randomly generated instances of the feature subscription problem.

The Computational Complexity of Dominance and Consistency in CP-Nets

We investigate the computational complexity of testing dominance and consistency in CP-nets. Previously, the complexity of dominance has been determined for restricted classes in which the dependency graph of the CP-net is acyclic. However, there are preferences of interest that define cyclic dependency graphs; these are modeled with general CP-nets. In our main results, we show here that both dominance and consistency for general CP-nets are PSPACE-complete. We then consider the concept of strong dominance, dominance equivalence and dominance incomparability, and several notions of optimality, and identify the complexity of the corresponding decision problems. The reductions used in the proofs are from STRIPS planning, and thus reinforce the earlier established connections between both areas.

Rules, Belief Functions and Default Logic

This paper describes a natural framework for rules, based on belief functions, which includes a repre- sentation of numerical rules, default rules and rules allowing and rules not allowing contraposition. In particular it justifies the use of the Dempster-Shafer Theory for representing a particular class of rules, Belief calculated being a lower probability given certain independence assumptions on an underlying space. It shows how a belief function framework can be generalised to other logics, including a general Monte-Carlo algorithm for calculating belief, and how a version of Reiter's Default Logic can be seen as a limiting case of a belief function formalism.

A Monte-Carlo Algorithm for Dempster-Shafer Belief

A very computationally-efficient Monte-Carlo algorithm for the calculation of Dempster-Shafer belief is described. If Bel is the combination using Dempster's Rule of belief functions Bel, ..., Bel,7, then, for subset b of the frame C), Bel(b) can be calculated in time linear in 1(31 and m (given that the weight of conflict is bounded). The algorithm can also be used to improve the complexity of the Shenoy-Shafer algorithms on Markov trees, and be generalised to calculate Dempster-Shafer Belief over other logics.

The Assumptions Behind Dempster's Rule

This paper examines the concept of a combination rule for belief functions. It is shown that two fairly simple and apparently reasonable assumptions determine Dempster's rule, giving a new justification for it.

Generating Graphoids from Generalised Conditional Probability

We take a general approach to uncertainty on product spaces, and give sufficient conditions for the independence structures of uncertainty measures to satisfy graphoid properties. Since these conditions are arguably more intuitive than some of the graphoid properties, they can be viewed as explanations why probability and certain other formalisms generate graphoids. The conditions include a sufficient condition for the Intersection property which can still apply even if there is a strong logical relations hip between the variables. We indicate how these results can be used to produce theories of qualitative conditional probability which are semi-graphoids and graphoids.

An Order of Magnitude Calculus

This paper develops a simple calculus for order of magnitude reasoning. A semantics is given with soundness and completeness results. Order of magnitude probability functions are easily defined and turn out to be equivalent to kappa functions, which are slight generalizations of Spohn's Natural Conditional Functions. The calculus also gives rise to an order of magnitude decision theory, which can be used to justify an amended version of Pearl's decision theory for kappa functions, although the latter is weaker and less expressive.