Using Non-Stationary Bandits for Learning in Repeated Cournot Games with Non-Stationary Demand

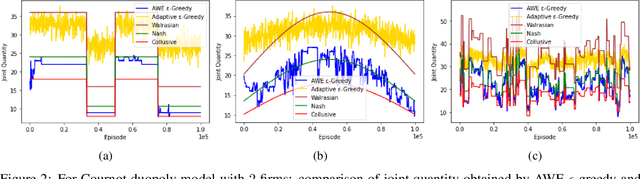
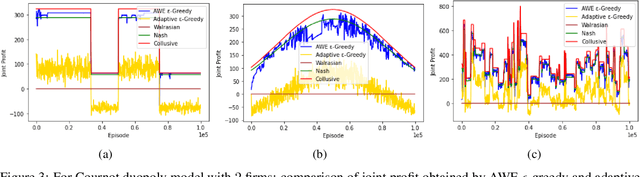
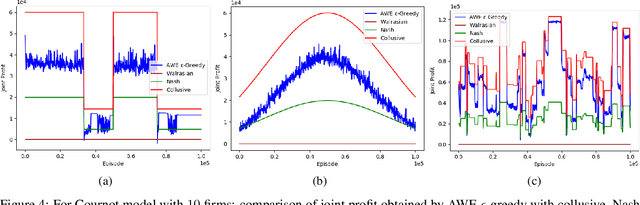
Many past attempts at modeling repeated Cournot games assume that demand is stationary. This does not align with real-world scenarios in which market demands can evolve over a product's lifetime for a myriad of reasons. In this paper, we model repeated Cournot games with non-stationary demand such that firms/agents face separate instances of non-stationary multi-armed bandit problem. The set of arms/actions that an agent can choose from represents discrete production quantities; here, the action space is ordered. Agents are independent and autonomous, and cannot observe anything from the environment; they can only see their own rewards after taking an action, and only work towards maximizing these rewards. We propose a novel algorithm 'Adaptive with Weighted Exploration (AWE) $\epsilon$-greedy' which is remotely based on the well-known $\epsilon$-greedy approach. This algorithm detects and quantifies changes in rewards due to varying market demand and varies learning rate and exploration rate in proportion to the degree of changes in demand, thus enabling agents to better identify new optimal actions. For efficient exploration, it also deploys a mechanism for weighing actions that takes advantage of the ordered action space. We use simulations to study the emergence of various equilibria in the market. In addition, we study the scalability of our approach in terms number of total agents in the system and the size of action space. We consider both symmetric and asymmetric firms in our models. We found that using our proposed method, agents are able to swiftly change their course of action according to the changes in demand, and they also engage in collusive behavior in many simulations.

Reinforcement Learning for Decentralized Stable Matching

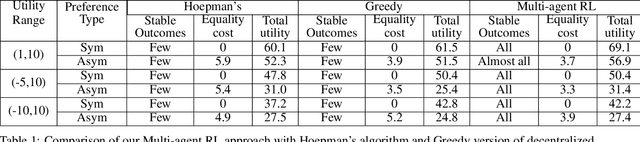
When it comes to finding a match/partner in the real world, it is usually an independent and autonomous task performed by people/entities. For a person, a match can be several things such as a romantic partner, business partner, school, roommate, etc. Our purpose in this paper is to train autonomous agents to find suitable matches for themselves using reinforcement learning. We consider the decentralized two-sided stable matching problem, where an agent is allowed to have at most one partner at a time from the opposite set. Each agent receives some utility for being in a match with a member of the opposite set. We formulate the problem spatially as a grid world environment and having autonomous agents acting independently makes our environment very uncertain and dynamic. We run experiments with various instances of both complete and incomplete weighted preference lists for agents. Agents learn their policies separately, using separate training modules. Our goal is to train agents to find partners such that the outcome is a stable matching if one exists and also a matching with set-equality, meaning the outcome is approximately equally likable by agents from both the sets.

The Complexity of Campaigning

In "The Logic of Campaigning", Dean and Parikh consider a candidate making campaign statements to appeal to the voters. They model these statements as Boolean formulas over variables that represent stances on the issues, and study optimal candidate strategies under three proposed models of voter preferences based on the assignments that satisfy these formulas. We prove that voter utility evaluation is computationally hard under these preference models (in one case, #P-hard), along with certain problems related to candidate strategic reasoning. Our results raise questions about the desirable characteristics of a voter preference model and to what extent a polynomial-time-evaluable function can capture them.

Ethical Considerations in Artificial Intelligence Courses

The recent surge in interest in ethics in artificial intelligence may leave many educators wondering how to address moral, ethical, and philosophical issues in their AI courses. As instructors we want to develop curriculum that not only prepares students to be artificial intelligence practitioners, but also to understand the moral, ethical, and philosophical impacts that artificial intelligence will have on society. In this article we provide practical case studies and links to resources for use by AI educators. We also provide concrete suggestions on how to integrate AI ethics into a general artificial intelligence course and how to teach a stand-alone artificial intelligence ethics course.

Topological Value Iteration Algorithms

Value iteration is a powerful yet inefficient algorithm for Markov decision processes (MDPs) because it puts the majority of its effort into backing up the entire state space, which turns out to be unnecessary in many cases. In order to overcome this problem, many approaches have been proposed. Among them, ILAO* and variants of RTDP are state-of-the-art ones. These methods use reachability analysis and heuristic search to avoid some unnecessary backups. However, none of these approaches build the graphical structure of the state transitions in a pre-processing step or use the structural information to systematically decompose a problem, whereby generating an intelligent backup sequence of the state space. In this paper, we present two optimal MDP algorithms. The first algorithm, topological value iteration (TVI), detects the structure of MDPs and backs up states based on topological sequences. It (1) divides an MDP into strongly-connected components (SCCs), and (2) solves these components sequentially. TVI outperforms VI and other state-of-the-art algorithms vastly when an MDP has multiple, close-to-equal-sized SCCs. The second algorithm, focused topological value iteration (FTVI), is an extension of TVI. FTVI restricts its attention to connected components that are relevant for solving the MDP. Specifically, it uses a small amount of heuristic search to eliminate provably sub-optimal actions; this pruning allows FTVI to find smaller connected components, thus running faster. We demonstrate that FTVI outperforms TVI by an order of magnitude, averaged across several domains. Surprisingly, FTVI also significantly outperforms popular heuristically-informed MDP algorithms such as ILAO*, LRTDP, BRTDP and Bayesian-RTDP in many domains, sometimes by as much as two orders of magnitude. Finally, we characterize the type of domains where FTVI excels --- suggesting a way to an informed choice of solver.

The Computational Complexity of Dominance and Consistency in CP-Nets

We investigate the computational complexity of testing dominance and consistency in CP-nets. Previously, the complexity of dominance has been determined for restricted classes in which the dependency graph of the CP-net is acyclic. However, there are preferences of interest that define cyclic dependency graphs; these are modeled with general CP-nets. In our main results, we show here that both dominance and consistency for general CP-nets are PSPACE-complete. We then consider the concept of strong dominance, dominance equivalence and dominance incomparability, and several notions of optimality, and identify the complexity of the corresponding decision problems. The reductions used in the proofs are from STRIPS planning, and thus reinforce the earlier established connections between both areas.

Approximation of Lorenz-Optimal Solutions in Multiobjective Markov Decision Processes

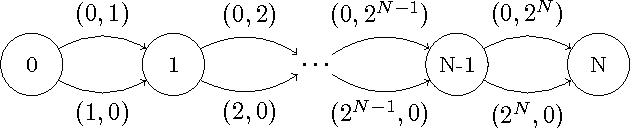
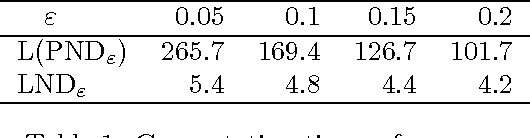
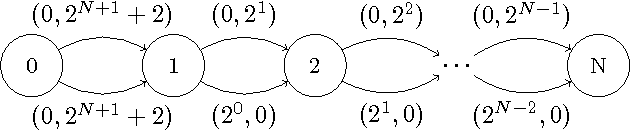
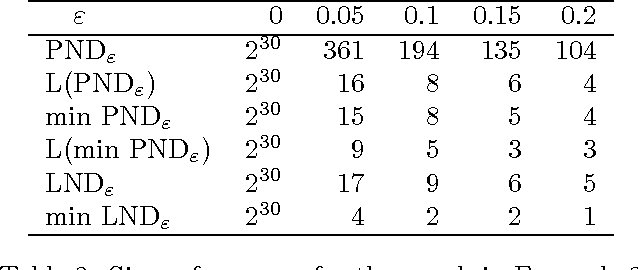
This paper is devoted to fair optimization in Multiobjective Markov Decision Processes (MOMDPs). A MOMDP is an extension of the MDP model for planning under uncertainty while trying to optimize several reward functions simultaneously. This applies to multiagent problems when rewards define individual utility functions, or in multicriteria problems when rewards refer to different features. In this setting, we study the determination of policies leading to Lorenz-non-dominated tradeoffs. Lorenz dominance is a refinement of Pareto dominance that was introduced in Social Choice for the measurement of inequalities. In this paper, we introduce methods to efficiently approximate the sets of Lorenz-non-dominated solutions of infinite-horizon, discounted MOMDPs. The approximations are polynomial-sized subsets of those solutions.

The Complexity of Plan Existence and Evaluation in Probabilistic Domains

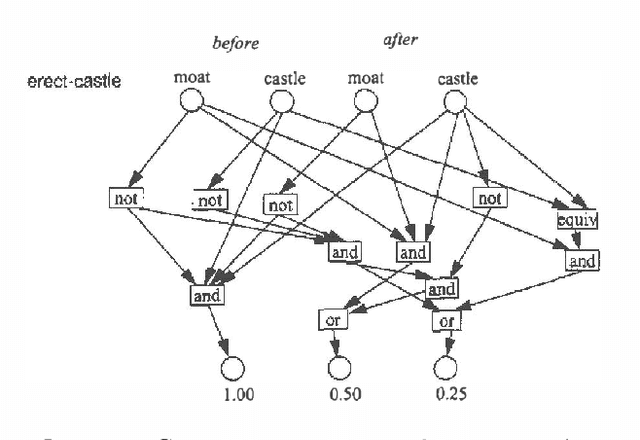
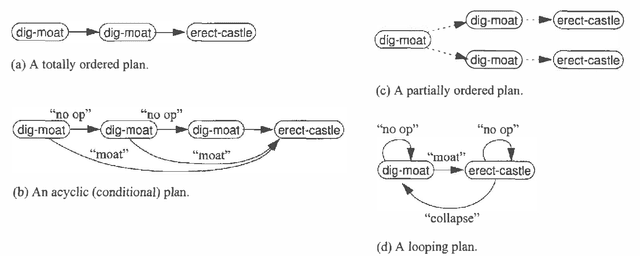
We examine the computational complexity of testing and finding small plans in probabilistic planning domains with succinct representations. We find that many problems of interest are complete for a variety of complexity classes: NP, co-NP, PP, NP^PP, co-NP^PP, and PSPACE. Of these, the probabilistic classes PP and NP^PP are likely to be of special interest in the field of uncertainty in artificial intelligence and are deserving of additional study. These results suggest a fruitful direction of future algorithmic development.

My Brain is Full: When More Memory Helps

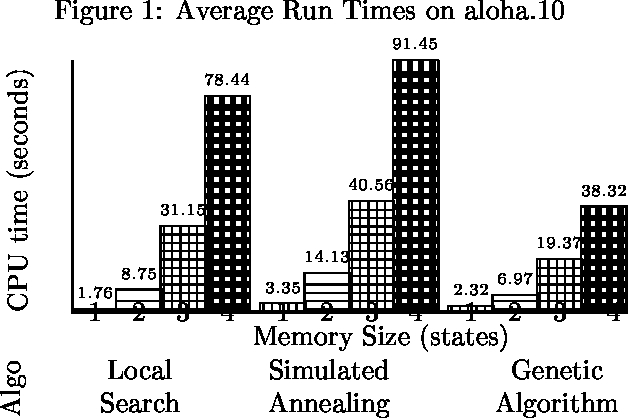
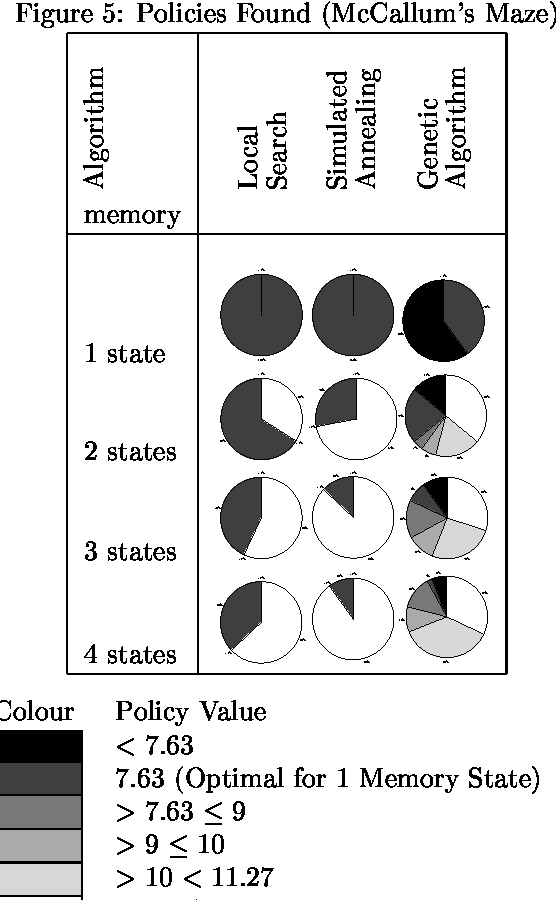
We consider the problem of finding good finite-horizon policies for POMDPs under the expected reward metric. The policies considered are {em free finite-memory policies with limited memory}; a policy is a mapping from the space of observation-memory pairs to the space of action-memeory pairs (the policy updates the memory as it goes), and the number of possible memory states is a parameter of the input to the policy-finding algorithms. The algorithms considered here are preliminary implementations of three search heuristics: local search, simulated annealing, and genetic algorithms. We compare their outcomes to each other and to the optimal policies for each instance. We compare run times of each policy and of a dynamic programming algorithm for POMDPs developed by Hansen that iteratively improves a finite-state controller --- the previous state of the art for finite memory policies. The value of the best policy can only improve as the amount of memory increases, up to the amount needed for an optimal finite-memory policy. Our most surprising finding is that more memory helps in another way: given more memory than is needed for an optimal policy, the algorithms are more likely to converge to optimal-valued policies.