My Brain is Full: When More Memory Helps
Paper and Code
Jan 23, 2013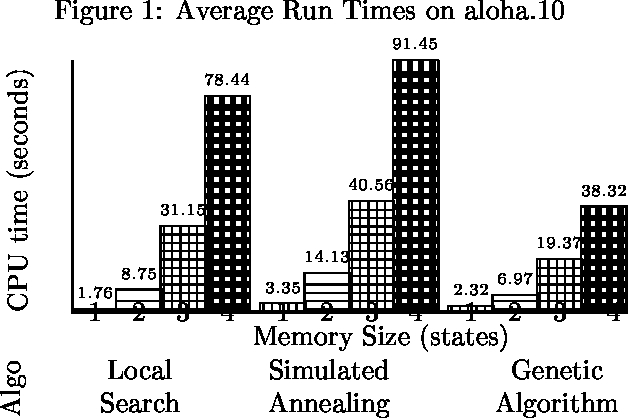
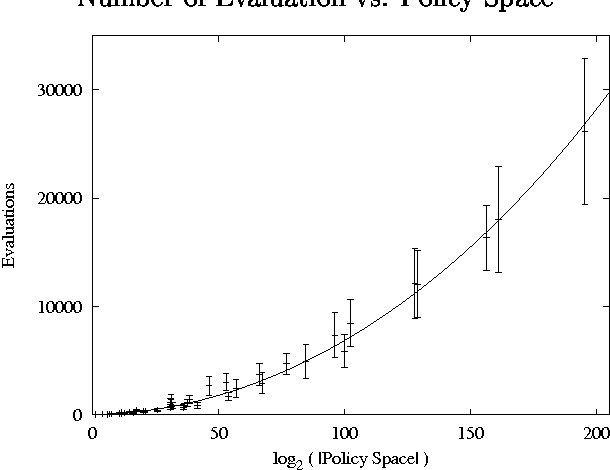
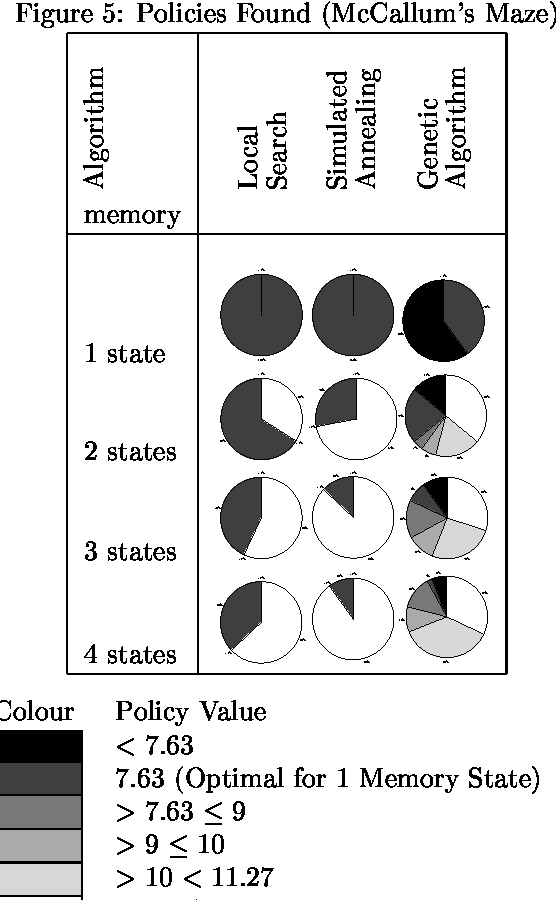
We consider the problem of finding good finite-horizon policies for POMDPs under the expected reward metric. The policies considered are {em free finite-memory policies with limited memory}; a policy is a mapping from the space of observation-memory pairs to the space of action-memeory pairs (the policy updates the memory as it goes), and the number of possible memory states is a parameter of the input to the policy-finding algorithms. The algorithms considered here are preliminary implementations of three search heuristics: local search, simulated annealing, and genetic algorithms. We compare their outcomes to each other and to the optimal policies for each instance. We compare run times of each policy and of a dynamic programming algorithm for POMDPs developed by Hansen that iteratively improves a finite-state controller --- the previous state of the art for finite memory policies. The value of the best policy can only improve as the amount of memory increases, up to the amount needed for an optimal finite-memory policy. Our most surprising finding is that more memory helps in another way: given more memory than is needed for an optimal policy, the algorithms are more likely to converge to optimal-valued policies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge