The Complexity of Plan Existence and Evaluation in Probabilistic Domains
Paper and Code
Feb 06, 2013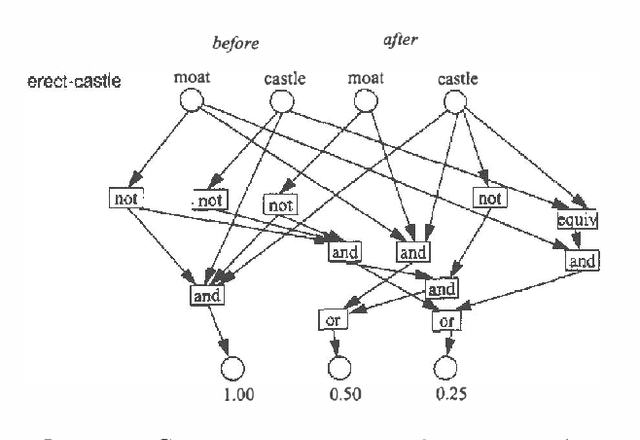

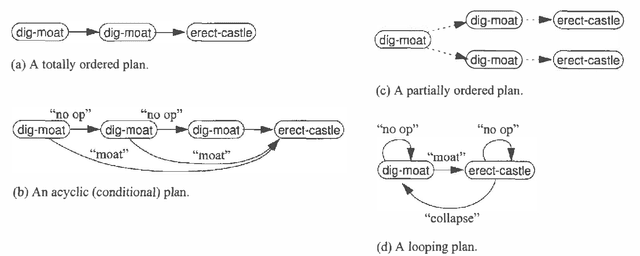

We examine the computational complexity of testing and finding small plans in probabilistic planning domains with succinct representations. We find that many problems of interest are complete for a variety of complexity classes: NP, co-NP, PP, NP^PP, co-NP^PP, and PSPACE. Of these, the probabilistic classes PP and NP^PP are likely to be of special interest in the field of uncertainty in artificial intelligence and are deserving of additional study. These results suggest a fruitful direction of future algorithmic development.
* Appears in Proceedings of the Thirteenth Conference on Uncertainty in
Artificial Intelligence (UAI1997)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge