Playing games with Large language models: Randomness and strategy

Playing games has a long history of describing intricate interactions in simplified forms. In this paper we explore if large language models (LLMs) can play games, investigating their capabilities for randomisation and strategic adaptation through both simultaneous and sequential game interactions. We focus on GPT-4o-Mini-2024-08-17 and test two games between LLMs: Rock Paper Scissors (RPS) and games of strategy (Prisoners Dilemma PD). LLMs are often described as stochastic parrots, and while they may indeed be parrots, our results suggest that they are not very stochastic in the sense that their outputs - when prompted to be random - are often very biased. Our research reveals that LLMs appear to develop loss aversion strategies in repeated games, with RPS converging to stalemate conditions while PD shows systematic shifts between cooperative and competitive outcomes based on prompt design. We detail programmatic tools for independent agent interactions and the Agentic AI challenges faced in implementation. We show that LLMs can indeed play games, just not very well. These results have implications for the use of LLMs in multi-agent LLM systems and showcase limitations in current approaches to model output for strategic decision-making.

Timetable Nodes for Public Transport Network

Faster pathfinding in time-dependent transport networks is an important and challenging problem in navigation systems. There are two main types of transport networks: road networks for car driving and public transport route network. The solutions that work well in road networks, such as Time-dependent Contraction Hierarchies and other graph-based approaches, do not usually apply in transport networks. In transport networks, non-graph solutions such as CSA and RAPTOR show the best results compared to graph-based techniques. In our work, we propose a method that advances graph-based approaches by using different optimization techniques from computational geometry to speed up the search process in transport networks. We apply a new pre-computation step, which we call timetable nodes (TTN). Our inspiration comes from an iterative search problem in computational geometry. We implement two versions of the TTN: one uses a Combined Search Tree (TTN-CST), and the second uses Fractional Cascading (TTN-FC). Both of these approaches decrease the asymptotic complexity of reaching new nodes from $O(k\times \log|C|)$ to $O(k + \log(k) + \log(|C|))$, where $k$ is the number of outgoing edges from a node and $|C|$ is the size of the timetable information (total outgoing edges). Our solution suits any other time-dependent networks and can be integrated into other pathfinding algorithms. Our experiments indicate that this pre-computation significantly enhances the performance on high-density graphs. This study showcases how leveraging computational geometry can enhance pathfinding in transport networks, enabling faster pathfinding in scenarios involving large numbers of outgoing edges.

Modelling Opaque Bilateral Market Dynamics in Financial Trading: Insights from a Multi-Agent Simulation Study

Exploring complex adaptive financial trading environments through multi-agent based simulation methods presents an innovative approach within the realm of quantitative finance. Despite the dominance of multi-agent reinforcement learning approaches in financial markets with observable data, there exists a set of systematically significant financial markets that pose challenges due to their partial or obscured data availability. We, therefore, devise a multi-agent simulation approach employing small-scale meta-heuristic methods. This approach aims to represent the opaque bilateral market for Australian government bond trading, capturing the bilateral nature of bank-to-bank trading, also referred to as "over-the-counter" (OTC) trading, and commonly occurring between "market makers". The uniqueness of the bilateral market, characterized by negotiated transactions and a limited number of agents, yields valuable insights for agent-based modelling and quantitative finance. The inherent rigidity of this market structure, which is at odds with the global proliferation of multilateral platforms and the decentralization of finance, underscores the unique insights offered by our agent-based model. We explore the implications of market rigidity on market structure and consider the element of stability, in market design. This extends the ongoing discourse on complex financial trading environments, providing an enhanced understanding of their dynamics and implications.

Nash Welfare and Facility Location

We consider the problem of locating a facility to serve a set of agents located along a line. The Nash welfare objective function, defined as the product of the agents' utilities, is known to provide a compromise between fairness and efficiency in resource allocation problems. We apply this welfare notion to the facility location problem, converting individual costs to utilities and analyzing the facility placement that maximizes the Nash welfare. We give a polynomial-time approximation algorithm to compute this facility location, and prove results suggesting that it achieves a good balance of fairness and efficiency. Finally, we take a mechanism design perspective and propose a strategy-proof mechanism with a bounded approximation ratio for Nash welfare.

Mechanisms that play a game, not toss a coin

Randomized mechanisms can have good normative properties compared to their deterministic counterparts. However, randomized mechanisms are problematic in several ways such as in their verifiability. We propose here to derandomize such mechanisms by having agents play a game instead of tossing a coin. The game is designed so an agent's best action is to play randomly, and this play then injects ``randomness'' into the mechanism. This derandomization retains many of the good normative properties of the original randomized mechanism but gives a mechanism that is deterministic and easy, for instance, to audit. We consider three related methods to derandomize randomized mechanism in six different domains: voting, facility location, task allocation, school choice, peer selection, and resource allocation. We propose a number of novel derandomized mechanisms for these six domains with good normative properties. Each mechanism has a mixed Nash equilibrium in which agents play a modular arithmetic game with an uniform mixed strategy. In all but one mixed Nash equilibrium, agents report their preferences over the original problem sincerely. The derandomized methods are thus ``quasi-strategy proof''. In one domain, we additionally show that a new and desirable normative property emerges as a result of derandomization.

Incentives to Offer Algorithmic Recourse

Due to the importance of artificial intelligence (AI) in a variety of high-stakes decisions, such as loan approval, job hiring, and criminal bail, researchers in Explainable AI (XAI) have developed algorithms to provide users with recourse for an unfavorable outcome. We analyze the incentives for a decision-maker to offer recourse to a set of applicants. Does the decision-maker have the incentive to offer recourse to all rejected applicants? We show that the decision-maker only offers recourse to all applicants in extreme cases, such as when the recourse process is impossible to manipulate. Some applicants may be worse off when the decision-maker can offer recourse.

Proportional Fairness in Obnoxious Facility Location

We consider the obnoxious facility location problem (in which agents prefer the facility location to be far from them) and propose a hierarchy of distance-based proportional fairness concepts for the problem. These fairness axioms ensure that groups of agents at the same location are guaranteed to be a distance from the facility proportional to their group size. We consider deterministic and randomized mechanisms, and compute tight bounds on the price of proportional fairness. In the deterministic setting, not only are our proportional fairness axioms incompatible with strategyproofness, the Nash equilibria may not guarantee welfare within a constant factor of the optimal welfare. On the other hand, in the randomized setting, we identify proportionally fair and strategyproof mechanisms that give an expected welfare within a constant factor of the optimal welfare.

Gathering Strength, Gathering Storms: The One Hundred Year Study on Artificial Intelligence (AI100) 2021 Study Panel Report

In September 2021, the "One Hundred Year Study on Artificial Intelligence" project (AI100) issued the second report of its planned long-term periodic assessment of artificial intelligence (AI) and its impact on society. It was written by a panel of 17 study authors, each of whom is deeply rooted in AI research, chaired by Michael Littman of Brown University. The report, entitled "Gathering Strength, Gathering Storms," answers a set of 14 questions probing critical areas of AI development addressing the major risks and dangers of AI, its effects on society, its public perception and the future of the field. The report concludes that AI has made a major leap from the lab to people's lives in recent years, which increases the urgency to understand its potential negative effects. The questions were developed by the AI100 Standing Committee, chaired by Peter Stone of the University of Texas at Austin, consisting of a group of AI leaders with expertise in computer science, sociology, ethics, economics, and other disciplines.

Manipulation and Peer Mechanisms: A Survey

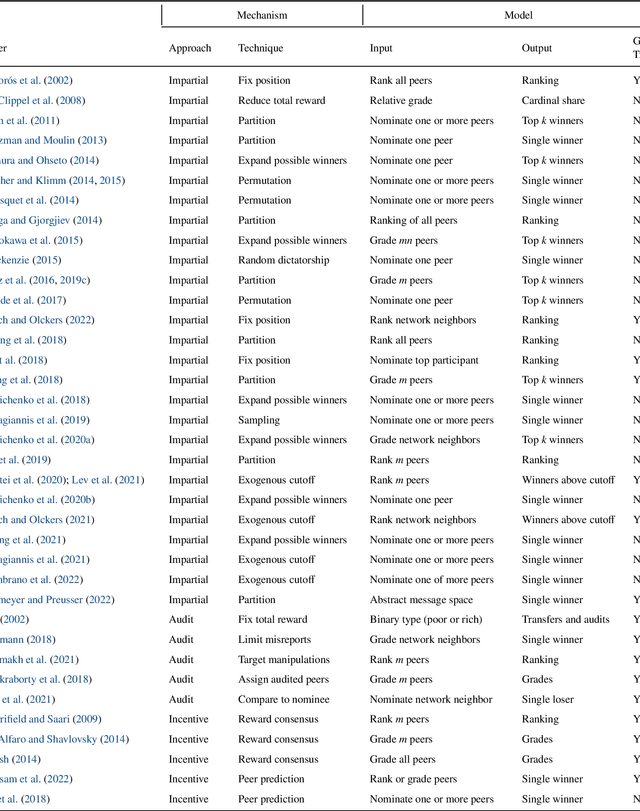
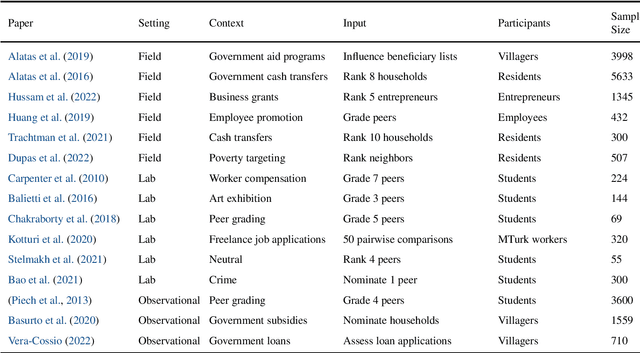
In peer mechanisms, the competitors for a prize also determine who wins. Each competitor may be asked to rank, grade, or nominate peers for the prize. Since the prize can be valuable, such as financial aid, course grades, or an award at a conference, competitors may be tempted to manipulate the mechanism. We survey approaches to prevent or discourage the manipulation of peer mechanisms. We conclude our survey by identifying several important research challenges

Random Rank: The One and Only Strategyproof and Proportionally Fair Randomized Facility Location Mechanism

Proportionality is an attractive fairness concept that has been applied to a range of problems including the facility location problem, a classic problem in social choice. In our work, we propose a concept called Strong Proportionality, which ensures that when there are two groups of agents at different locations, both groups incur the same total cost. We show that although Strong Proportionality is a well-motivated and basic axiom, there is no deterministic strategyproof mechanism satisfying the property. We then identify a randomized mechanism called Random Rank (which uniformly selects a number $k$ between $1$ to $n$ and locates the facility at the $k$'th highest agent location) which satisfies Strong Proportionality in expectation. Our main theorem characterizes Random Rank as the unique mechanism that achieves universal truthfulness, universal anonymity, and Strong Proportionality in expectation among all randomized mechanisms. Finally, we show via the AverageOrRandomRank mechanism that even stronger ex-post fairness guarantees can be achieved by weakening universal truthfulness to strategyproofness in expectation.