CompassJudger-1: All-in-one Judge Model Helps Model Evaluation and Evolution

Efficient and accurate evaluation is crucial for the continuous improvement of large language models (LLMs). Among various assessment methods, subjective evaluation has garnered significant attention due to its superior alignment with real-world usage scenarios and human preferences. However, human-based evaluations are costly and lack reproducibility, making precise automated evaluators (judgers) vital in this process. In this report, we introduce \textbf{CompassJudger-1}, the first open-source \textbf{all-in-one} judge LLM. CompassJudger-1 is a general-purpose LLM that demonstrates remarkable versatility. It is capable of: 1. Performing unitary scoring and two-model comparisons as a reward model; 2. Conducting evaluations according to specified formats; 3. Generating critiques; 4. Executing diverse tasks like a general LLM. To assess the evaluation capabilities of different judge models under a unified setting, we have also established \textbf{JudgerBench}, a new benchmark that encompasses various subjective evaluation tasks and covers a wide range of topics. CompassJudger-1 offers a comprehensive solution for various evaluation tasks while maintaining the flexibility to adapt to diverse requirements. Both CompassJudger and JudgerBench are released and available to the research community athttps://github.com/open-compass/CompassJudger. We believe that by open-sourcing these tools, we can foster collaboration and accelerate progress in LLM evaluation methodologies.

Temporal Fair Division of Indivisible Items

We study a fair division model where indivisible items arrive sequentially, and must be allocated immediately and irrevocably. Previous work on online fair division has shown impossibility results in achieving approximate envy-freeness under these constraints. In contrast, we consider an informed setting where the algorithm has complete knowledge of future items, and aim to ensure that the cumulative allocation at each round satisfies approximate envy-freeness -- which we define as temporal envy-freeness up to one item (TEF1). We focus on settings where items can be exclusively goods or exclusively chores. For goods, while TEF1 allocations may not always exist, we identify several special cases where they do -- two agents, two item types, generalized binary valuations, unimodal preferences -- and provide polynomial-time algorithms for these cases. We also prove that determining the existence of a TEF1 allocation is NP-hard. For chores, we establish analogous results for the special cases, but present a slightly weaker intractability result. We also establish the incompatibility between TEF1 and Pareto-optimality, with the implication that it is intractable to find a TEF1 allocation that maximizes any $p$-mean welfare, even for two agents.

Facility Location Games with Scaling Effects

We take the classic facility location problem and consider a variation, in which each agent's individual cost function is equal to their distance from the facility multiplied by a scaling factor which is determined by the facility placement. In addition to the general class of continuous scaling functions, we also provide results for piecewise linear scaling functions which can effectively approximate or model the scaling of many real world scenarios. We focus on the objectives of total and maximum cost, describing the computation of the optimal solution. We then move to the approximate mechanism design setting, observing that the agents' preferences may no longer be single-peaked. Consequently, we characterize the conditions on scaling functions which ensure that agents have single-peaked preferences. Under these conditions, we find results on the total and maximum cost approximation ratios achievable by strategyproof and anonymous mechanisms.

Nash Welfare and Facility Location

We consider the problem of locating a facility to serve a set of agents located along a line. The Nash welfare objective function, defined as the product of the agents' utilities, is known to provide a compromise between fairness and efficiency in resource allocation problems. We apply this welfare notion to the facility location problem, converting individual costs to utilities and analyzing the facility placement that maximizes the Nash welfare. We give a polynomial-time approximation algorithm to compute this facility location, and prove results suggesting that it achieves a good balance of fairness and efficiency. Finally, we take a mechanism design perspective and propose a strategy-proof mechanism with a bounded approximation ratio for Nash welfare.

Proportional Fairness in Obnoxious Facility Location

We consider the obnoxious facility location problem (in which agents prefer the facility location to be far from them) and propose a hierarchy of distance-based proportional fairness concepts for the problem. These fairness axioms ensure that groups of agents at the same location are guaranteed to be a distance from the facility proportional to their group size. We consider deterministic and randomized mechanisms, and compute tight bounds on the price of proportional fairness. In the deterministic setting, not only are our proportional fairness axioms incompatible with strategyproofness, the Nash equilibria may not guarantee welfare within a constant factor of the optimal welfare. On the other hand, in the randomized setting, we identify proportionally fair and strategyproof mechanisms that give an expected welfare within a constant factor of the optimal welfare.

Random Rank: The One and Only Strategyproof and Proportionally Fair Randomized Facility Location Mechanism

Proportionality is an attractive fairness concept that has been applied to a range of problems including the facility location problem, a classic problem in social choice. In our work, we propose a concept called Strong Proportionality, which ensures that when there are two groups of agents at different locations, both groups incur the same total cost. We show that although Strong Proportionality is a well-motivated and basic axiom, there is no deterministic strategyproof mechanism satisfying the property. We then identify a randomized mechanism called Random Rank (which uniformly selects a number $k$ between $1$ to $n$ and locates the facility at the $k$'th highest agent location) which satisfies Strong Proportionality in expectation. Our main theorem characterizes Random Rank as the unique mechanism that achieves universal truthfulness, universal anonymity, and Strong Proportionality in expectation among all randomized mechanisms. Finally, we show via the AverageOrRandomRank mechanism that even stronger ex-post fairness guarantees can be achieved by weakening universal truthfulness to strategyproofness in expectation.

Obvious Manipulability of Voting Rules

The Gibbard-Satterthwaite theorem states that no unanimous and non-dictatorial voting rule is strategyproof. We revisit voting rules and consider a weaker notion of strategyproofness called not obvious manipulability that was proposed by Troyan and Morrill (2020). We identify several classes of voting rules that satisfy this notion. We also show that several voting rules including k-approval fail to satisfy this property. We characterize conditions under which voting rules are obviously manipulable. One of our insights is that certain rules are obviously manipulable when the number of alternatives is relatively large compared to the number of voters. In contrast to the Gibbard-Satterthwaite theorem, many of the rules we examined are not obviously manipulable. This reflects the relatively easier satisfiability of the notion and the zero information assumption of not obvious manipulability, as opposed to the perfect information assumption of strategyproofness. We also present algorithmic results for computing obvious manipulations and report on experiments.

Strategyproof and Proportionally Fair Facility Location

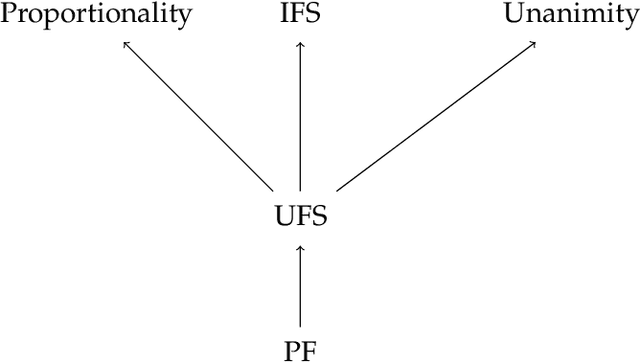
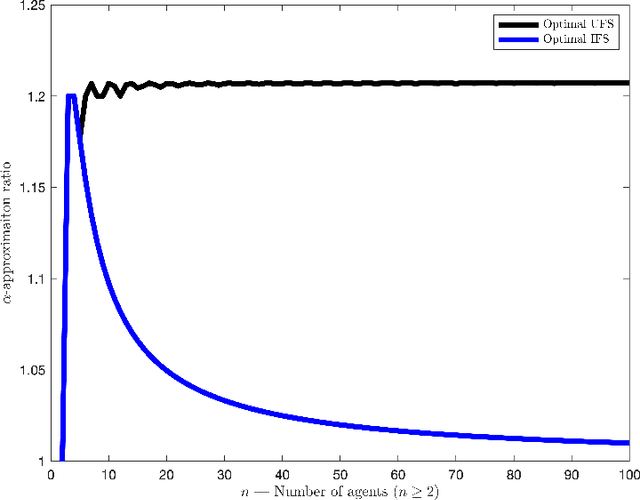
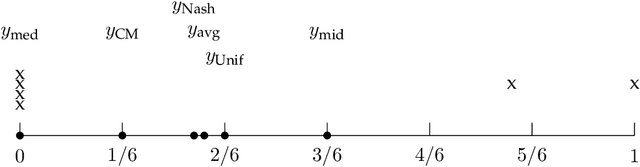
We focus on a simple, one-dimensional collective decision problem (often referred to as the facility location problem) and explore issues of strategyproofness and proportional fairness. We present several characterization results for mechanisms that satisfy strategyproofness and varying levels of proportional fairness. We also characterize one of the mechanisms as the unique equilibrium outcome for any mechanism that satisfies natural fairness and monotonicity properties. Finally, we identify strategyproof and proportionally fair mechanisms that provide the best welfare-optimal approximation among all mechanisms that satisfy the corresponding fairness axiom.