Fair Division with Market Values

We introduce a model of fair division with market values, where indivisible goods must be partitioned among agents with (additive) subjective valuations, and each good additionally has a market value. The market valuation can be viewed as a separate additive valuation that holds identically across all the agents. We seek allocations that are simultaneously fair with respect to the subjective valuations and with respect to the market valuation. We show that an allocation that satisfies stochastically-dominant envy-freeness up to one good (SD-EF1) with respect to both the subjective valuations and the market valuation does not always exist, but the weaker guarantee of EF1 with respect to the subjective valuations along with SD-EF1 with respect to the market valuation can be guaranteed. We also study a number of other guarantees such as Pareto optimality, EFX, and MMS. In addition, we explore non-additive valuations and extend our model to cake-cutting. Along the way, we identify several tantalizing open questions.

Temporal Fair Division of Indivisible Items

We study a fair division model where indivisible items arrive sequentially, and must be allocated immediately and irrevocably. Previous work on online fair division has shown impossibility results in achieving approximate envy-freeness under these constraints. In contrast, we consider an informed setting where the algorithm has complete knowledge of future items, and aim to ensure that the cumulative allocation at each round satisfies approximate envy-freeness -- which we define as temporal envy-freeness up to one item (TEF1). We focus on settings where items can be exclusively goods or exclusively chores. For goods, while TEF1 allocations may not always exist, we identify several special cases where they do -- two agents, two item types, generalized binary valuations, unimodal preferences -- and provide polynomial-time algorithms for these cases. We also prove that determining the existence of a TEF1 allocation is NP-hard. For chores, we establish analogous results for the special cases, but present a slightly weaker intractability result. We also establish the incompatibility between TEF1 and Pareto-optimality, with the implication that it is intractable to find a TEF1 allocation that maximizes any $p$-mean welfare, even for two agents.

Best of Both Distortion Worlds

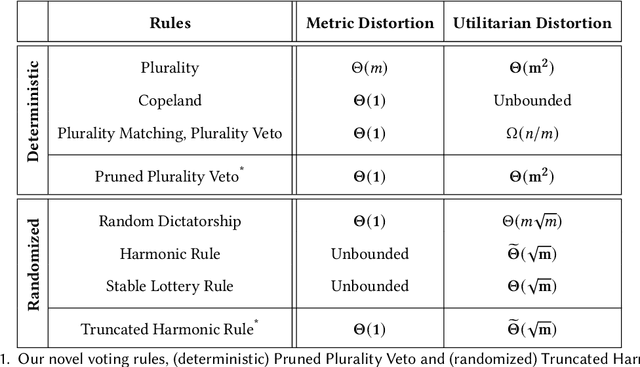
We study the problem of designing voting rules that take as input the ordinal preferences of $n$ agents over a set of $m$ alternatives and output a single alternative, aiming to optimize the overall happiness of the agents. The input to the voting rule is each agent's ranking of the alternatives from most to least preferred, yet the agents have more refined (cardinal) preferences that capture the intensity with which they prefer one alternative over another. To quantify the extent to which voting rules can optimize over the cardinal preferences given access only to the ordinal ones, prior work has used the distortion measure, i.e., the worst-case approximation ratio between a voting rule's performance and the best performance achievable given the cardinal preferences. The work on the distortion of voting rules has been largely divided into two worlds: utilitarian distortion and metric distortion. In the former, the cardinal preferences of the agents correspond to general utilities and the goal is to maximize a normalized social welfare. In the latter, the agents' cardinal preferences correspond to costs given by distances in an underlying metric space and the goal is to minimize the (unnormalized) social cost. Several deterministic and randomized voting rules have been proposed and evaluated for each of these worlds separately, gradually improving the achievable distortion bounds, but none of the known voting rules perform well in both worlds simultaneously. In this work, we prove that one can achieve the best of both worlds by designing new voting rules, that simultaneously achieve near-optimal distortion guarantees in both distortion worlds. We also prove that this positive result does not generalize to the case where the voting rule is provided with the rankings of only the top-$t$ alternatives of each agent, for $t<m$.