Policy Aggregation

We consider the challenge of AI value alignment with multiple individuals that have different reward functions and optimal policies in an underlying Markov decision process. We formalize this problem as one of policy aggregation, where the goal is to identify a desirable collective policy. We argue that an approach informed by social choice theory is especially suitable. Our key insight is that social choice methods can be reinterpreted by identifying ordinal preferences with volumes of subsets of the state-action occupancy polytope. Building on this insight, we demonstrate that a variety of methods--including approval voting, Borda count, the proportional veto core, and quantile fairness--can be practically applied to policy aggregation.

Fair Division with Market Values

We introduce a model of fair division with market values, where indivisible goods must be partitioned among agents with (additive) subjective valuations, and each good additionally has a market value. The market valuation can be viewed as a separate additive valuation that holds identically across all the agents. We seek allocations that are simultaneously fair with respect to the subjective valuations and with respect to the market valuation. We show that an allocation that satisfies stochastically-dominant envy-freeness up to one good (SD-EF1) with respect to both the subjective valuations and the market valuation does not always exist, but the weaker guarantee of EF1 with respect to the subjective valuations along with SD-EF1 with respect to the market valuation can be guaranteed. We also study a number of other guarantees such as Pareto optimality, EFX, and MMS. In addition, we explore non-additive valuations and extend our model to cake-cutting. Along the way, we identify several tantalizing open questions.

Harm Ratio: A Novel and Versatile Fairness Criterion

Envy-freeness has become the cornerstone of fair division research. In settings where each individual is allocated a disjoint share of collective resources, it is a compelling fairness axiom which demands that no individual strictly prefer the allocation of another individual to their own. Unfortunately, in many real-life collective decision-making problems, the goal is to choose a (common) public outcome that is equally applicable to all individuals, and the notion of envy becomes vacuous. Consequently, this literature has avoided studying fairness criteria that focus on individuals feeling a sense of jealousy or resentment towards other individuals (rather than towards the system), missing out on a key aspect of fairness. In this work, we propose a novel fairness criterion, individual harm ratio, which is inspired by envy-freeness but applies to a broad range of collective decision-making settings. Theoretically, we identify minimal conditions under which this criterion and its groupwise extensions can be guaranteed, and study the computational complexity of related problems. Empirically, we conduct experiments with real data to show that our fairness criterion is powerful enough to differentiate between prominent decision-making algorithms for a range of tasks from voting and fair division to participatory budgeting and peer review.

Fast Algorithm for K-Truss Discovery on Public-Private Graphs

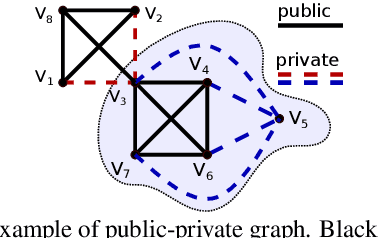
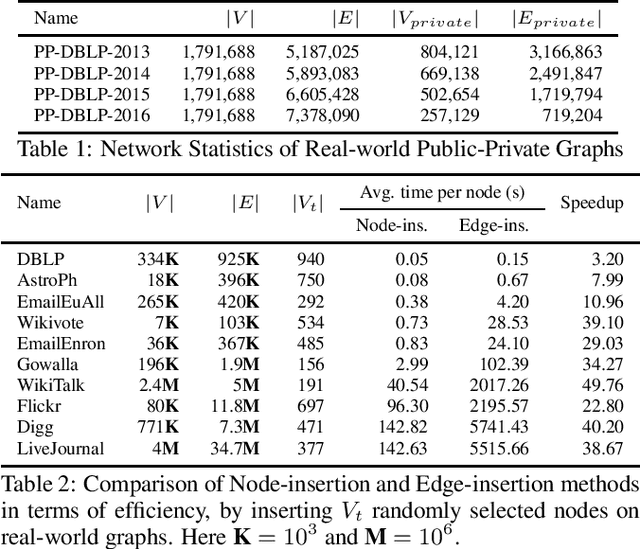
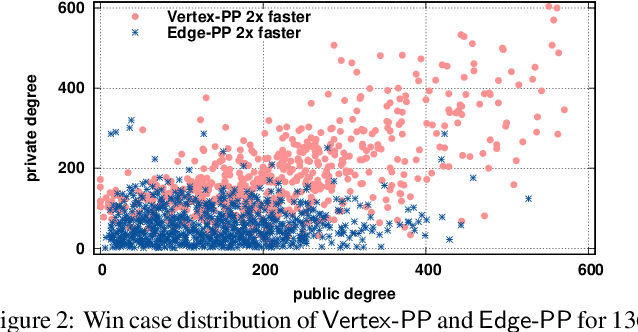
In public-private graphs, users share one public graph and have their own private graphs. A private graph consists of personal private contacts that only can be visible to its owner, e.g., hidden friend lists on Facebook and secret following on Sina Weibo. However, existing public-private analytic algorithms have not yet investigated the dense subgraph discovery of k-truss, where each edge is contained in at least k-2 triangles. This paper aims at finding k-truss efficiently in public-private graphs. The core of our solution is a novel algorithm to update k-truss with node insertions. We develop a classification-based hybrid strategy of node insertions and edge insertions to incrementally compute k-truss in public-private graphs. Extensive experiments validate the superiority of our proposed algorithms against state-of-the-art methods on real-world datasets.