Harm Ratio: A Novel and Versatile Fairness Criterion

Envy-freeness has become the cornerstone of fair division research. In settings where each individual is allocated a disjoint share of collective resources, it is a compelling fairness axiom which demands that no individual strictly prefer the allocation of another individual to their own. Unfortunately, in many real-life collective decision-making problems, the goal is to choose a (common) public outcome that is equally applicable to all individuals, and the notion of envy becomes vacuous. Consequently, this literature has avoided studying fairness criteria that focus on individuals feeling a sense of jealousy or resentment towards other individuals (rather than towards the system), missing out on a key aspect of fairness. In this work, we propose a novel fairness criterion, individual harm ratio, which is inspired by envy-freeness but applies to a broad range of collective decision-making settings. Theoretically, we identify minimal conditions under which this criterion and its groupwise extensions can be guaranteed, and study the computational complexity of related problems. Empirically, we conduct experiments with real data to show that our fairness criterion is powerful enough to differentiate between prominent decision-making algorithms for a range of tasks from voting and fair division to participatory budgeting and peer review.

Two-Sided Matching Meets Fair Division

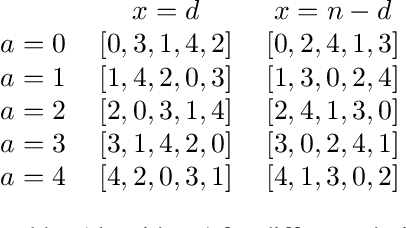
We introduce a new model for two-sided matching which allows us to borrow popular fairness notions from the fair division literature such as envy-freeness up to one good and maximin share guarantee. In our model, each agent is matched to multiple agents on the other side over whom she has additive preferences. We demand fairness for each side separately, giving rise to notions such as double envy-freeness up to one match (DEF1) and double maximin share guarantee (DMMS). We show that (a slight strengthening of) DEF1 cannot always be achieved, but in the special case where both sides have identical preferences, the round-robin algorithm with a carefully designed agent ordering achieves it. In contrast, DMMS cannot be achieved even when both sides have identical preferences.

No-Regret and Incentive-Compatible Online Learning

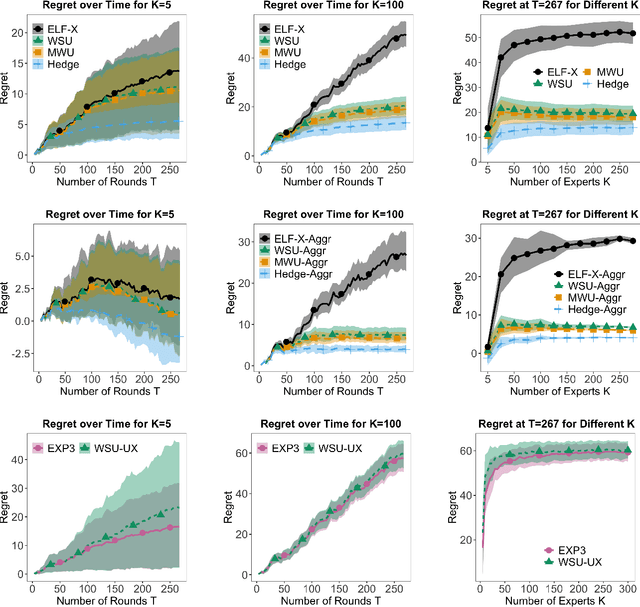
We study online learning settings in which experts act strategically to maximize their influence on the learning algorithm's predictions by potentially misreporting their beliefs about a sequence of binary events. Our goal is twofold. First, we want the learning algorithm to be no-regret with respect to the best fixed expert in hindsight. Second, we want incentive compatibility, a guarantee that each expert's best strategy is to report his true beliefs about the realization of each event. To achieve this goal, we build on the literature on wagering mechanisms, a type of multi-agent scoring rule. We provide algorithms that achieve no regret and incentive compatibility for myopic experts for both the full and partial information settings. In experiments on datasets from FiveThirtyEight, our algorithms have regret comparable to classic no-regret algorithms, which are not incentive-compatible. Finally, we identify an incentive-compatible algorithm for forward-looking strategic agents that exhibits diminishing regret in practice.

Crowdsourced Outcome Determination in Prediction Markets

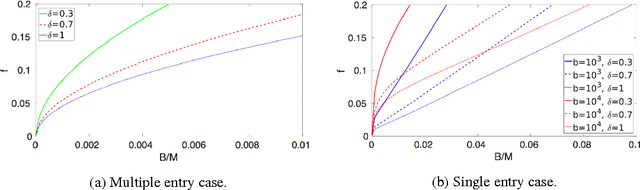
A prediction market is a useful means of aggregating information about a future event. To function, the market needs a trusted entity who will verify the true outcome in the end. Motivated by the recent introduction of decentralized prediction markets, we introduce a mechanism that allows for the outcome to be determined by the votes of a group of arbiters who may themselves hold stakes in the market. Despite the potential conflict of interest, we derive conditions under which we can incentivize arbiters to vote truthfully by using funds raised from market fees to implement a peer prediction mechanism. Finally, we investigate what parameter values could be used in a real-world implementation of our mechanism.