Sebastien Lahaie
Synthetic Design: An Optimization Approach to Experimental Design with Synthetic Controls
Dec 01, 2021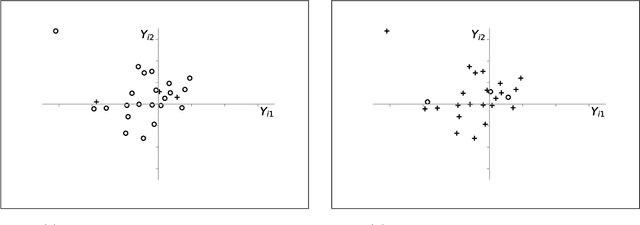
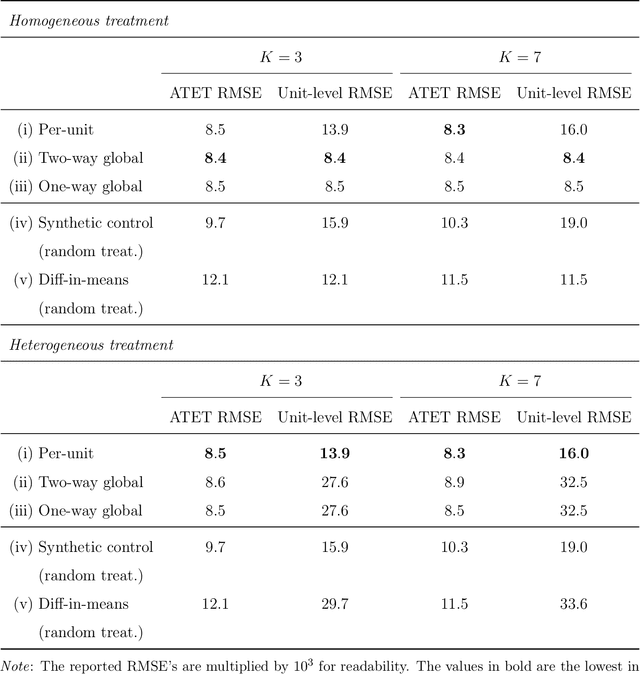
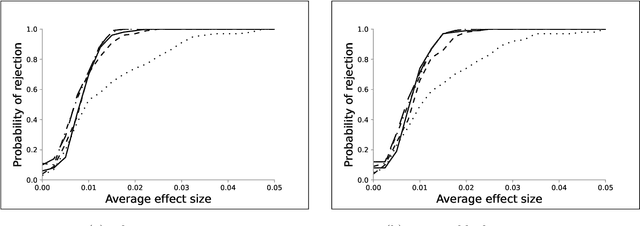
Abstract:We investigate the optimal design of experimental studies that have pre-treatment outcome data available. The average treatment effect is estimated as the difference between the weighted average outcomes of the treated and control units. A number of commonly used approaches fit this formulation, including the difference-in-means estimator and a variety of synthetic-control techniques. We propose several methods for choosing the set of treated units in conjunction with the weights. Observing the NP-hardness of the problem, we introduce a mixed-integer programming formulation which selects both the treatment and control sets and unit weightings. We prove that these proposed approaches lead to qualitatively different experimental units being selected for treatment. We use simulations based on publicly available data from the US Bureau of Labor Statistics that show improvements in terms of mean squared error and statistical power when compared to simple and commonly used alternatives such as randomized trials.
Crowdsourced Outcome Determination in Prediction Markets
Dec 14, 2016
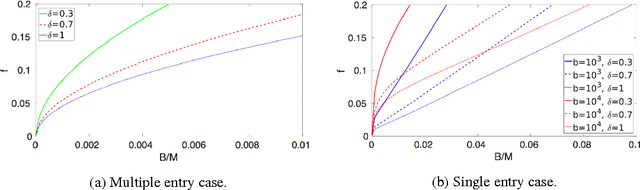
Abstract:A prediction market is a useful means of aggregating information about a future event. To function, the market needs a trusted entity who will verify the true outcome in the end. Motivated by the recent introduction of decentralized prediction markets, we introduce a mechanism that allows for the outcome to be determined by the votes of a group of arbiters who may themselves hold stakes in the market. Despite the potential conflict of interest, we derive conditions under which we can incentivize arbiters to vote truthfully by using funds raised from market fees to implement a peer prediction mechanism. Finally, we investigate what parameter values could be used in a real-world implementation of our mechanism.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge