Cascade-based Randomization for Inferring Causal Effects under Diffusion Interference

The presence of interference, where the outcome of an individual may depend on the treatment assignment and behavior of neighboring nodes, can lead to biased causal effect estimation. Current approaches to network experiment design focus on limiting interference through cluster-based randomization, in which clusters are identified using graph clustering, and cluster randomization dictates the node assignment to treatment and control. However, cluster-based randomization approaches perform poorly when interference propagates in cascades, whereby the response of individuals to treatment propagates to their multi-hop neighbors. When we have knowledge of the cascade seed nodes, we can leverage this interference structure to mitigate the resulting causal effect estimation bias. With this goal, we propose a cascade-based network experiment design that initiates treatment assignment from the cascade seed node and propagates the assignment to their multi-hop neighbors to limit interference during cascade growth and thereby reduce the overall causal effect estimation error. Our extensive experiments on real-world and synthetic datasets demonstrate that our proposed framework outperforms the existing state-of-the-art approaches in estimating causal effects in network data.

Causal Inference with Differentially Private (Clustered) Outcomes

Estimating causal effects from randomized experiments is only feasible if participants agree to reveal their potentially sensitive responses. Of the many ways of ensuring privacy, label differential privacy is a widely used measure of an algorithm's privacy guarantee, which might encourage participants to share responses without running the risk of de-anonymization. Many differentially private mechanisms inject noise into the original data-set to achieve this privacy guarantee, which increases the variance of most statistical estimators and makes the precise measurement of causal effects difficult: there exists a fundamental privacy-variance trade-off to performing causal analyses from differentially private data. With the aim of achieving lower variance for stronger privacy guarantees, we suggest a new differential privacy mechanism, "Cluster-DP", which leverages any given cluster structure of the data while still allowing for the estimation of causal effects. We show that, depending on an intuitive measure of cluster quality, we can improve the variance loss while maintaining our privacy guarantees. We compare its performance, theoretically and empirically, to that of its unclustered version and a more extreme uniform-prior version which does not use any of the original response distribution, both of which are special cases of the "Cluster-DP" algorithm.

Causal Estimation of User Learning in Personalized Systems

In online platforms, the impact of a treatment on an observed outcome may change over time as 1) users learn about the intervention, and 2) the system personalization, such as individualized recommendations, change over time. We introduce a non-parametric causal model of user actions in a personalized system. We show that the Cookie-Cookie-Day (CCD) experiment, designed for the measurement of the user learning effect, is biased when there is personalization. We derive new experimental designs that intervene in the personalization system to generate the variation necessary to separately identify the causal effect mediated through user learning and personalization. Making parametric assumptions allows for the estimation of long-term causal effects based on medium-term experiments. In simulations, we show that our new designs successfully recover the dynamic causal effects of interest.

Synthetic Design: An Optimization Approach to Experimental Design with Synthetic Controls

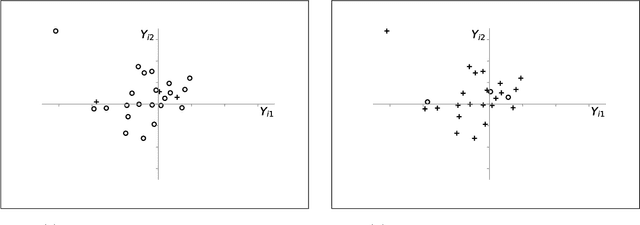
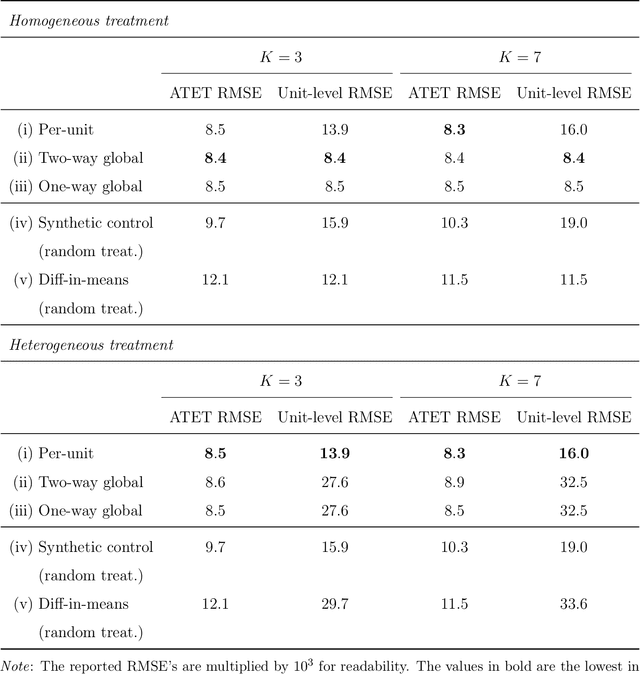
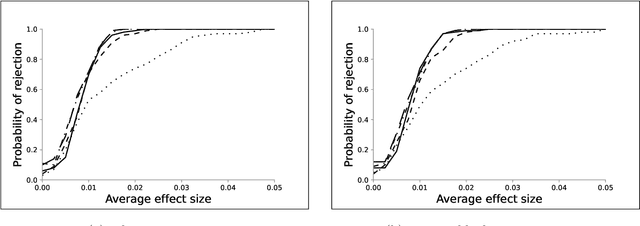
We investigate the optimal design of experimental studies that have pre-treatment outcome data available. The average treatment effect is estimated as the difference between the weighted average outcomes of the treated and control units. A number of commonly used approaches fit this formulation, including the difference-in-means estimator and a variety of synthetic-control techniques. We propose several methods for choosing the set of treated units in conjunction with the weights. Observing the NP-hardness of the problem, we introduce a mixed-integer programming formulation which selects both the treatment and control sets and unit weightings. We prove that these proposed approaches lead to qualitatively different experimental units being selected for treatment. We use simulations based on publicly available data from the US Bureau of Labor Statistics that show improvements in terms of mean squared error and statistical power when compared to simple and commonly used alternatives such as randomized trials.

Inferring Graphs from Cascades: A Sparse Recovery Framework

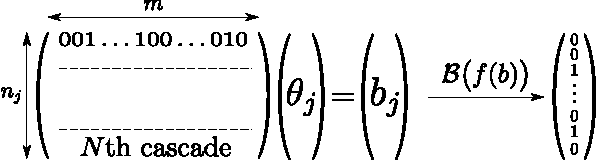
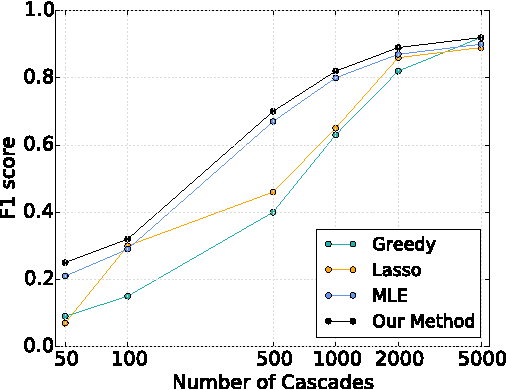
In the Network Inference problem, one seeks to recover the edges of an unknown graph from the observations of cascades propagating over this graph. In this paper, we approach this problem from the sparse recovery perspective. We introduce a general model of cascades, including the voter model and the independent cascade model, for which we provide the first algorithm which recovers the graph's edges with high probability and $O(s\log m)$ measurements where $s$ is the maximum degree of the graph and $m$ is the number of nodes. Furthermore, we show that our algorithm also recovers the edge weights (the parameters of the diffusion process) and is robust in the context of approximate sparsity. Finally we prove an almost matching lower bound of $\Omega(s\log\frac{m}{s})$ and validate our approach empirically on synthetic graphs.

Overcoming the Curse of Sentence Length for Neural Machine Translation using Automatic Segmentation

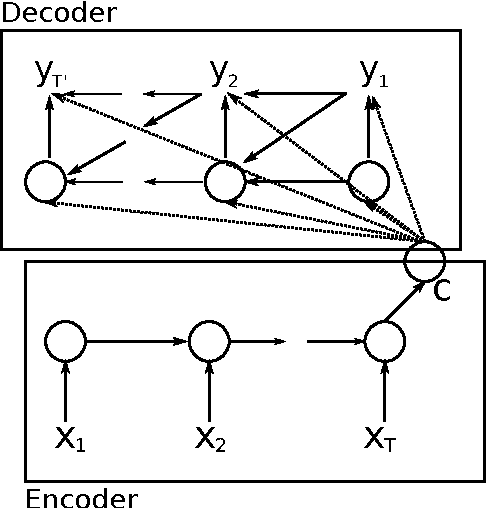
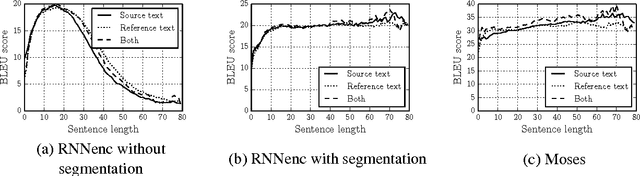
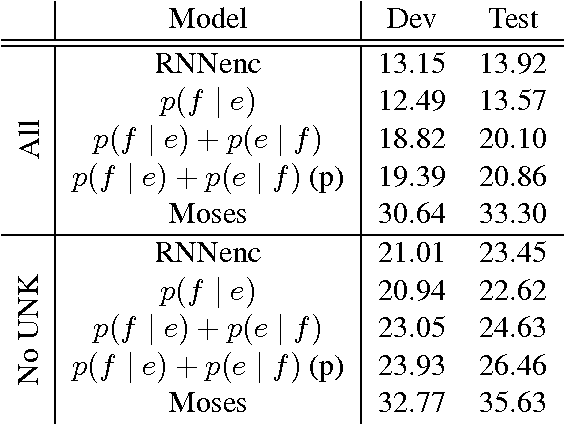
The authors of (Cho et al., 2014a) have shown that the recently introduced neural network translation systems suffer from a significant drop in translation quality when translating long sentences, unlike existing phrase-based translation systems. In this paper, we propose a way to address this issue by automatically segmenting an input sentence into phrases that can be easily translated by the neural network translation model. Once each segment has been independently translated by the neural machine translation model, the translated clauses are concatenated to form a final translation. Empirical results show a significant improvement in translation quality for long sentences.

Generative Adversarial Networks

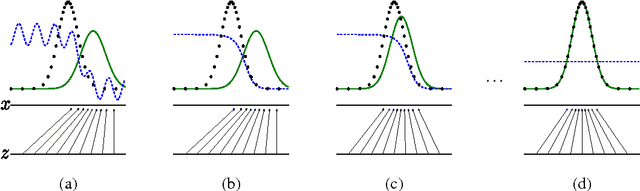
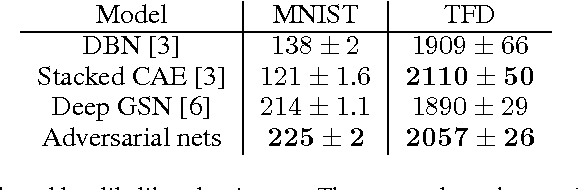
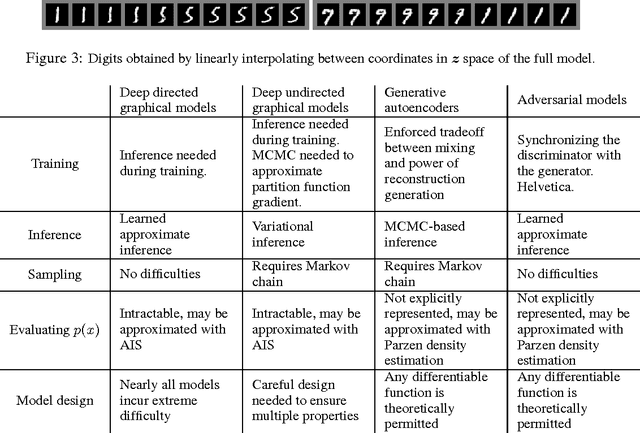
We propose a new framework for estimating generative models via an adversarial process, in which we simultaneously train two models: a generative model G that captures the data distribution, and a discriminative model D that estimates the probability that a sample came from the training data rather than G. The training procedure for G is to maximize the probability of D making a mistake. This framework corresponds to a minimax two-player game. In the space of arbitrary functions G and D, a unique solution exists, with G recovering the training data distribution and D equal to 1/2 everywhere. In the case where G and D are defined by multilayer perceptrons, the entire system can be trained with backpropagation. There is no need for any Markov chains or unrolled approximate inference networks during either training or generation of samples. Experiments demonstrate the potential of the framework through qualitative and quantitative evaluation of the generated samples.