Estimation of Models with Limited Data by Leveraging Shared Structure

Modern data sets, such as those in healthcare and e-commerce, are often derived from many individuals or systems but have insufficient data from each source alone to separately estimate individual, often high-dimensional, model parameters. If there is shared structure among systems however, it may be possible to leverage data from other systems to help estimate individual parameters, which could otherwise be non-identifiable. In this paper, we assume systems share a latent low-dimensional parameter space and propose a method for recovering $d$-dimensional parameters for $N$ different linear systems, even when there are only $T<d$ observations per system. To do so, we develop a three-step algorithm which estimates the low-dimensional subspace spanned by the systems' parameters and produces refined parameter estimates within the subspace. We provide finite sample subspace estimation error guarantees for our proposed method. Finally, we experimentally validate our method on simulations with i.i.d. regression data and as well as correlated time series data.

Optimal Bounds between $f$-Divergences and Integral Probability Metrics

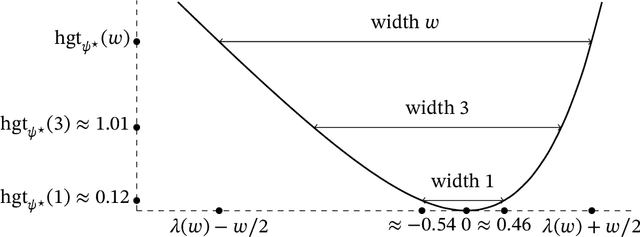
The families of $f$-divergences (e.g. the Kullback-Leibler divergence) and Integral Probability Metrics (e.g. total variation distance or maximum mean discrepancies) are commonly used in optimization and estimation. In this work, we systematically study the relationship between these two families from the perspective of convex duality. Starting from a tight variational representation of the $f$-divergence, we derive a generalization of the moment generating function, which we show exactly characterizes the best lower bound of the $f$-divergence as a function of a given IPM. Using this characterization, we obtain new bounds on IPMs defined by classes of unbounded functions, while also recovering in a unified manner well-known results for bounded and subgaussian functions (e.g. Pinsker's inequality and Hoeffding's lemma). The variational representation also allows us to prove new results on the topological properties of the divergence which may be of independent interest.

Stable Robbins-Monro approximations through stochastic proximal updates

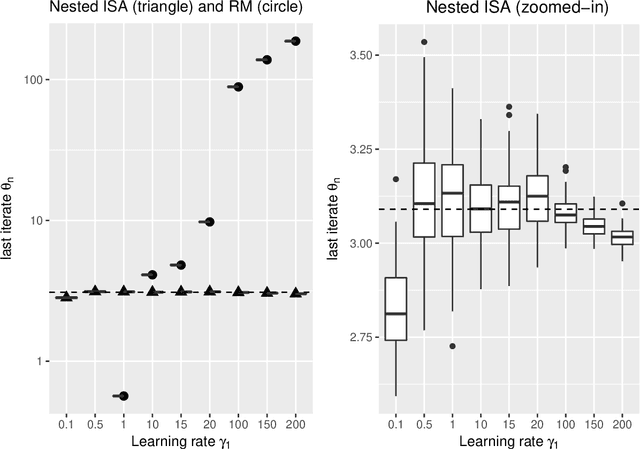
The need for parameter estimation with massive data has reinvigorated interest in iterative estimation procedures. Stochastic approximations, such as stochastic gradient descent, are at the forefront of this recent development because they yield simple, generic, and extremely fast iterative estimation procedures. Such stochastic approximations, however, are often numerically unstable. As a consequence, current practice has turned to proximal operators, which can induce stable parameter updates within iterations. While the majority of classical iterative estimation procedures are subsumed by the framework of Robbins and Monro (1951), there is no such generalization for stochastic approximations with proximal updates. In this paper, we conceptualize a general stochastic approximation method with proximal updates. This method can be applied even in situations where the analytical form of the objective is not known, and so it generalizes many stochastic gradient procedures with proximal operators currently in use. Our theoretical analysis indicates that the proposed method has important stability benefits over the classical stochastic approximation method. Exact instantiations of the proposed method are challenging, but we show that approximate instantiations lead to procedures that are easy to implement, and still dominate classical procedures by achieving numerical stability without tradeoffs. This last advantage is akin to that seen in deterministic proximal optimization, where the framework is typically impossible to instantiate exactly, but where approximate instantiations lead to new optimization procedures that dominate classical ones.

Inferring Graphs from Cascades: A Sparse Recovery Framework

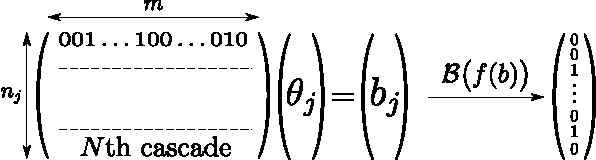
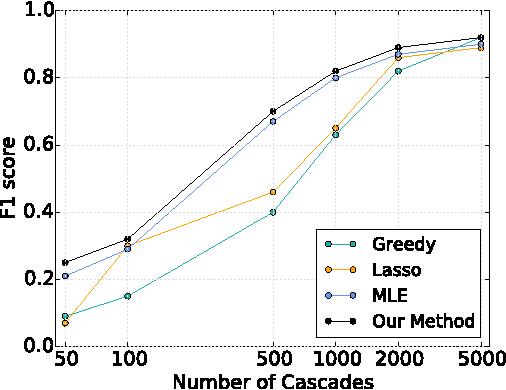
In the Network Inference problem, one seeks to recover the edges of an unknown graph from the observations of cascades propagating over this graph. In this paper, we approach this problem from the sparse recovery perspective. We introduce a general model of cascades, including the voter model and the independent cascade model, for which we provide the first algorithm which recovers the graph's edges with high probability and $O(s\log m)$ measurements where $s$ is the maximum degree of the graph and $m$ is the number of nodes. Furthermore, we show that our algorithm also recovers the edge weights (the parameters of the diffusion process) and is robust in the context of approximate sparsity. Finally we prove an almost matching lower bound of $\Omega(s\log\frac{m}{s})$ and validate our approach empirically on synthetic graphs.