Stacking Models for Nearly Optimal Link Prediction in Complex Networks

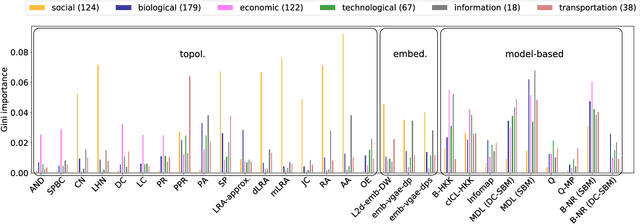
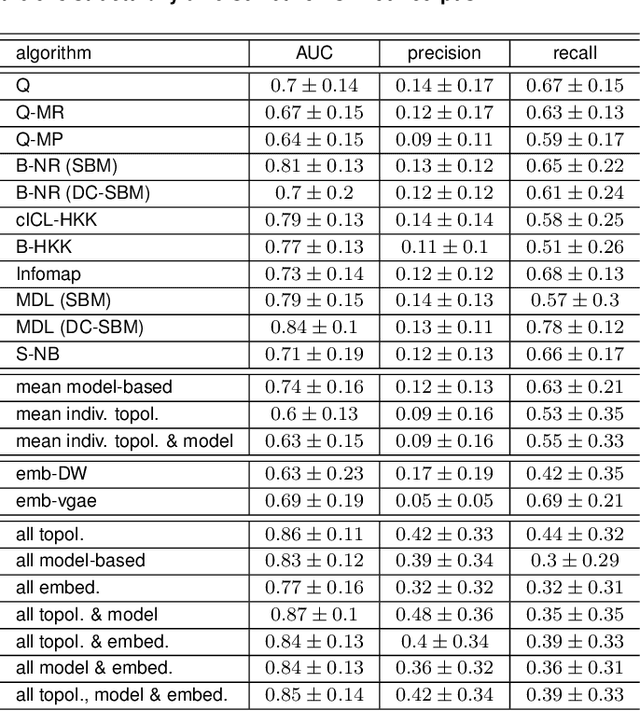
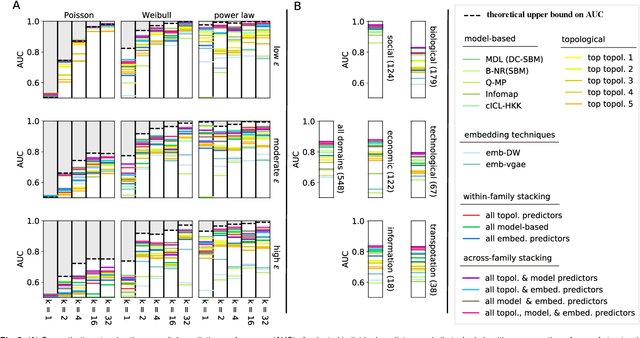
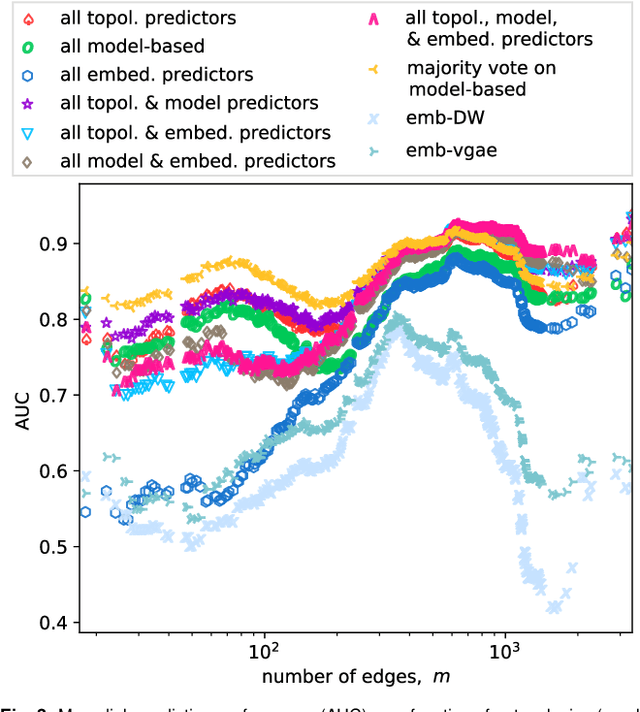
Most real-world networks are incompletely observed. Algorithms that can accurately predict which links are missing can dramatically speedup the collection of network data and improve the validity of network models. Many algorithms now exist for predicting missing links, given a partially observed network, but it has remained unknown whether a single best predictor exists, how link predictability varies across methods and networks from different domains, and how close to optimality current methods are. We answer these questions by systematically evaluating 203 individual link predictor algorithms, representing three popular families of methods, applied to a large corpus of 548 structurally diverse networks from six scientific domains. We first show that individual algorithms exhibit a broad diversity of prediction errors, such that no one predictor or family is best, or worst, across all realistic inputs. We then exploit this diversity via meta-learning to construct a series of "stacked" models that combine predictors into a single algorithm. Applied to a broad range of synthetic networks, for which we may analytically calculate optimal performance, these stacked models achieve optimal or nearly optimal levels of accuracy. Applied to real-world networks, stacked models are also superior, but their accuracy varies strongly by domain, suggesting that link prediction may be fundamentally easier in social networks than in biological or technological networks. These results indicate that the state-of-the-art for link prediction comes from combining individual algorithms, which achieves nearly optimal predictions. We close with a brief discussion of limitations and opportunities for further improvement of these results.

Stable Robbins-Monro approximations through stochastic proximal updates

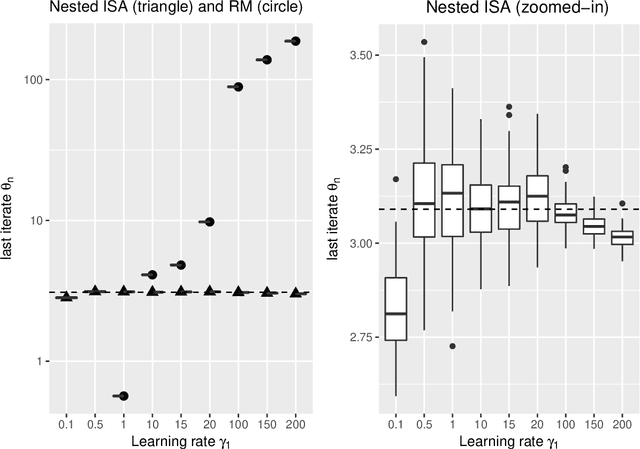
The need for parameter estimation with massive data has reinvigorated interest in iterative estimation procedures. Stochastic approximations, such as stochastic gradient descent, are at the forefront of this recent development because they yield simple, generic, and extremely fast iterative estimation procedures. Such stochastic approximations, however, are often numerically unstable. As a consequence, current practice has turned to proximal operators, which can induce stable parameter updates within iterations. While the majority of classical iterative estimation procedures are subsumed by the framework of Robbins and Monro (1951), there is no such generalization for stochastic approximations with proximal updates. In this paper, we conceptualize a general stochastic approximation method with proximal updates. This method can be applied even in situations where the analytical form of the objective is not known, and so it generalizes many stochastic gradient procedures with proximal operators currently in use. Our theoretical analysis indicates that the proposed method has important stability benefits over the classical stochastic approximation method. Exact instantiations of the proposed method are challenging, but we show that approximate instantiations lead to procedures that are easy to implement, and still dominate classical procedures by achieving numerical stability without tradeoffs. This last advantage is akin to that seen in deterministic proximal optimization, where the framework is typically impossible to instantiate exactly, but where approximate instantiations lead to new optimization procedures that dominate classical ones.

Model-assisted design of experiments in the presence of network correlated outcomes

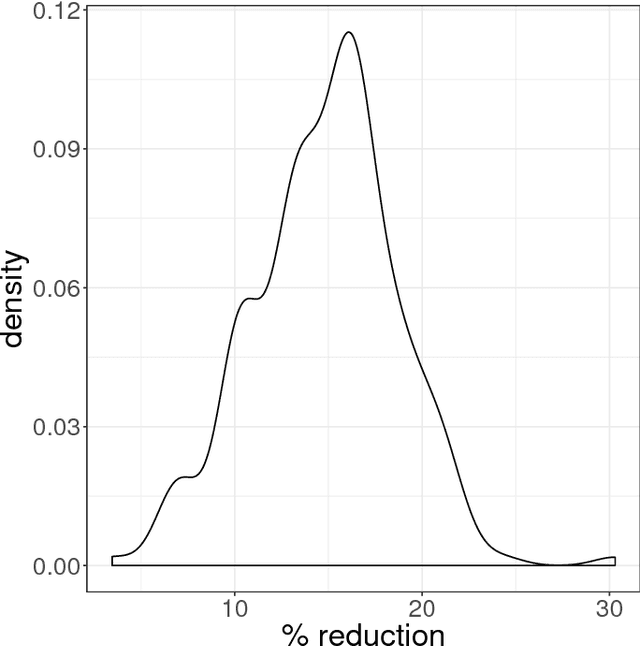
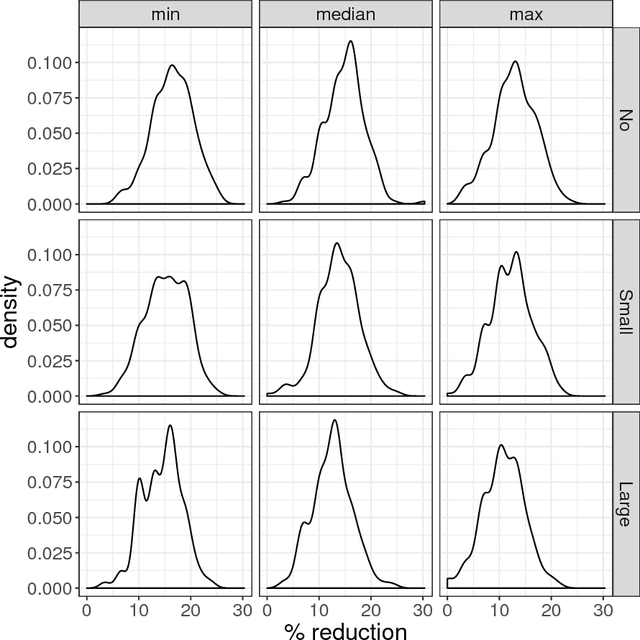
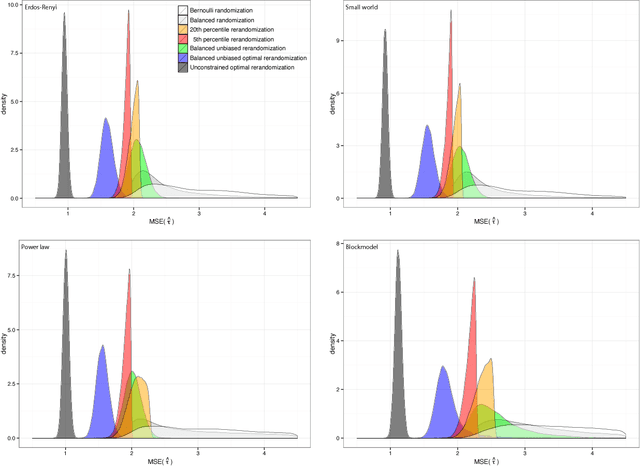
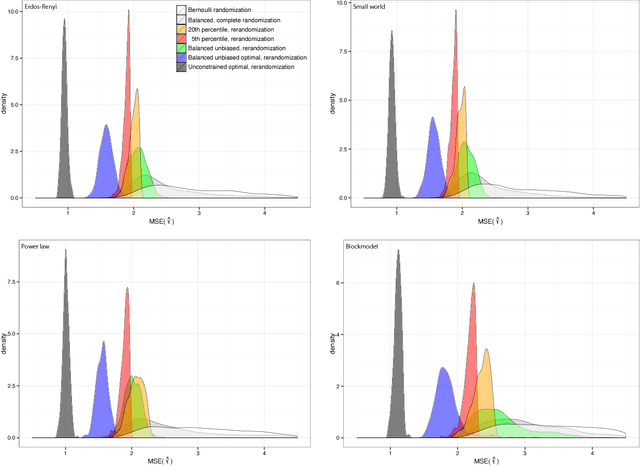
We consider the problem of how to assign treatment in a randomized experiment, in which the correlation among the outcomes is informed by a network available pre-intervention. Working within the potential outcome causal framework, we develop a class of models that posit such a correlation structure among the outcomes. Then we leverage these models to develop restricted randomization strategies for allocating treatment optimally, by minimizing the mean square error of the estimated average treatment effect. Analytical decompositions of the mean square error, due both to the model and to the randomization distribution, provide insights into aspects of the optimal designs. In particular, the analysis suggests new notions of balance based on specific network quantities, in addition to classical covariate balance. The resulting balanced, optimal restricted randomization strategies are still design unbiased, in situations where the model used to derive them does not hold. We illustrate how the proposed treatment allocation strategies improve on allocations that ignore the network structure, with extensive simulations.

Asymptotic and finite-sample properties of estimators based on stochastic gradients

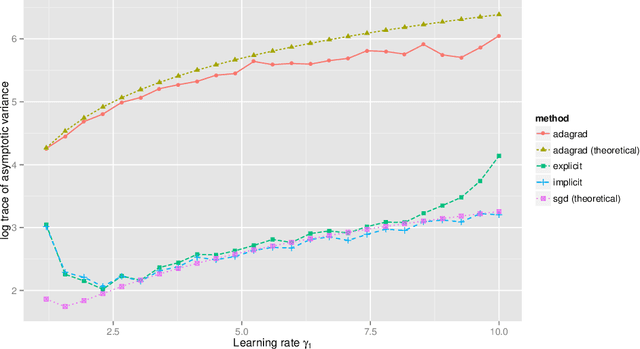
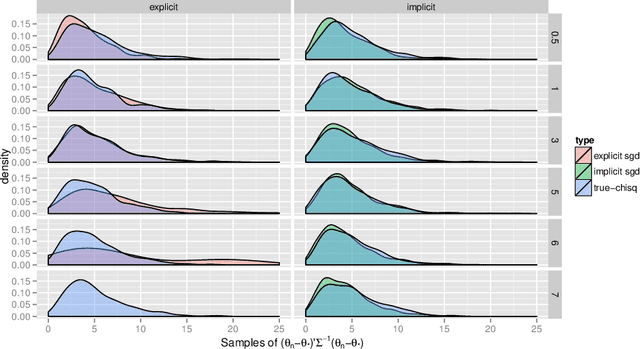
Stochastic gradient descent procedures have gained popularity for parameter estimation from large data sets. However, their statistical properties are not well understood, in theory. And in practice, avoiding numerical instability requires careful tuning of key parameters. Here, we introduce implicit stochastic gradient descent procedures, which involve parameter updates that are implicitly defined. Intuitively, implicit updates shrink standard stochastic gradient descent updates. The amount of shrinkage depends on the observed Fisher information matrix, which does not need to be explicitly computed; thus, implicit procedures increase stability without increasing the computational burden. Our theoretical analysis provides the first full characterization of the asymptotic behavior of both standard and implicit stochastic gradient descent-based estimators, including finite-sample error bounds. Importantly, analytical expressions for the variances of these stochastic gradient-based estimators reveal their exact loss of efficiency. We also develop new algorithms to compute implicit stochastic gradient descent-based estimators for generalized linear models, Cox proportional hazards, M-estimators, in practice, and perform extensive experiments. Our results suggest that implicit stochastic gradient descent procedures are poised to become a workhorse for approximate inference from large data sets

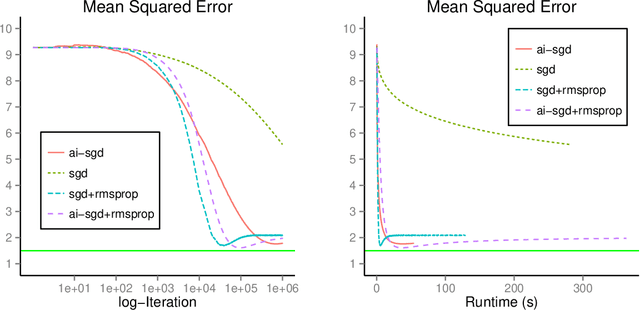
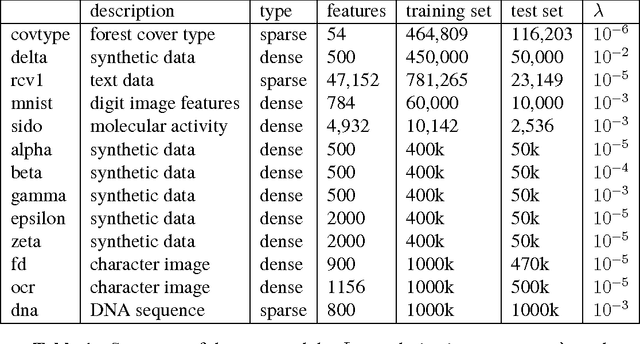
Towards stability and optimality in stochastic gradient descent

Iterative procedures for parameter estimation based on stochastic gradient descent allow the estimation to scale to massive data sets. However, in both theory and practice, they suffer from numerical instability. Moreover, they are statistically inefficient as estimators of the true parameter value. To address these two issues, we propose a new iterative procedure termed averaged implicit SGD (AI-SGD). For statistical efficiency, AI-SGD employs averaging of the iterates, which achieves the optimal Cram\'{e}r-Rao bound under strong convexity, i.e., it is an optimal unbiased estimator of the true parameter value. For numerical stability, AI-SGD employs an implicit update at each iteration, which is related to proximal operators in optimization. In practice, AI-SGD achieves competitive performance with other state-of-the-art procedures. Furthermore, it is more stable than averaging procedures that do not employ proximal updates, and is simple to implement as it requires fewer tunable hyperparameters than procedures that do employ proximal updates.

Copula variational inference

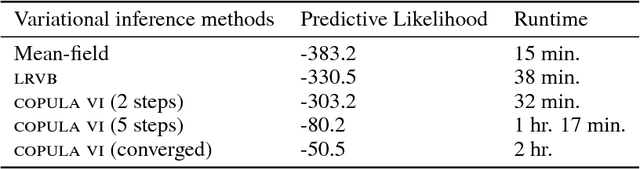
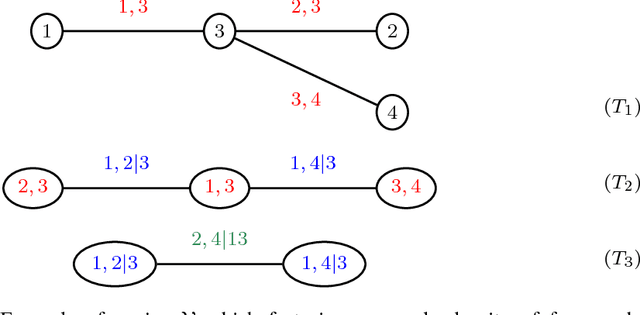
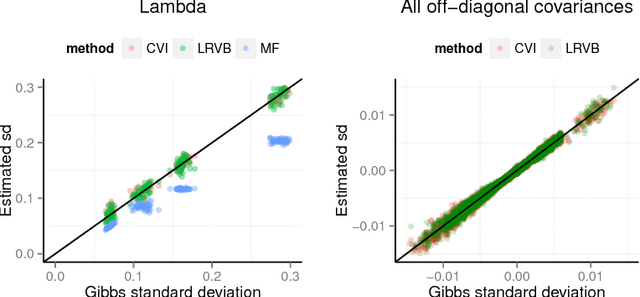
We develop a general variational inference method that preserves dependency among the latent variables. Our method uses copulas to augment the families of distributions used in mean-field and structured approximations. Copulas model the dependency that is not captured by the original variational distribution, and thus the augmented variational family guarantees better approximations to the posterior. With stochastic optimization, inference on the augmented distribution is scalable. Furthermore, our strategy is generic: it can be applied to any inference procedure that currently uses the mean-field or structured approach. Copula variational inference has many advantages: it reduces bias; it is less sensitive to local optima; it is less sensitive to hyperparameters; and it helps characterize and interpret the dependency among the latent variables.

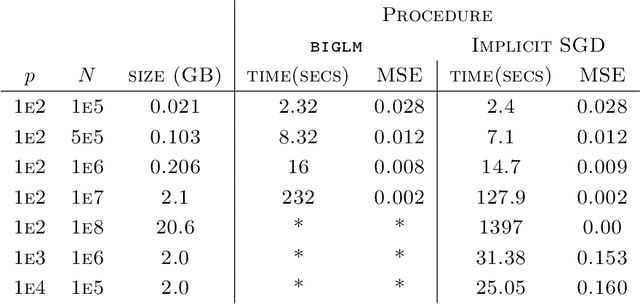
Stochastic gradient descent methods for estimation with large data sets

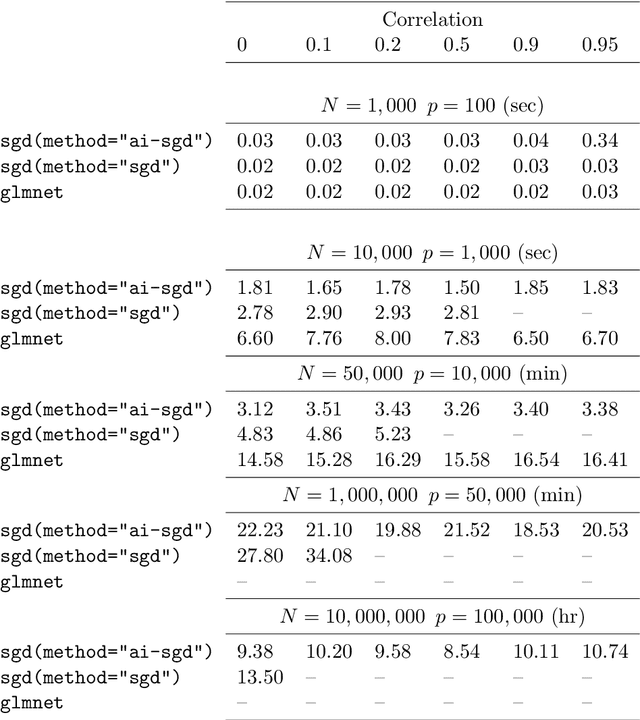
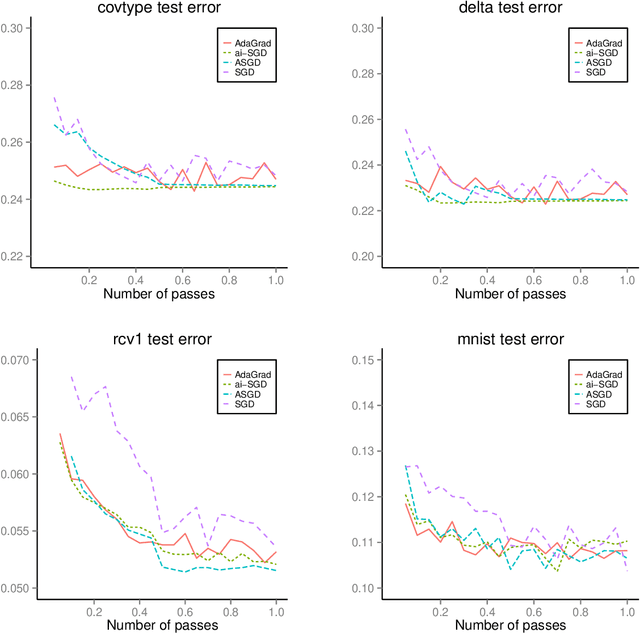
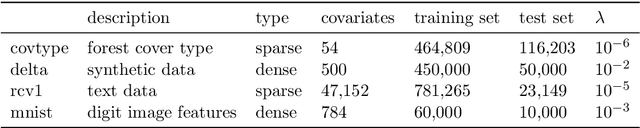
We develop methods for parameter estimation in settings with large-scale data sets, where traditional methods are no longer tenable. Our methods rely on stochastic approximations, which are computationally efficient as they maintain one iterate as a parameter estimate, and successively update that iterate based on a single data point. When the update is based on a noisy gradient, the stochastic approximation is known as standard stochastic gradient descent, which has been fundamental in modern applications with large data sets. Additionally, our methods are numerically stable because they employ implicit updates of the iterates. Intuitively, an implicit update is a shrinked version of a standard one, where the shrinkage factor depends on the observed Fisher information at the corresponding data point. This shrinkage prevents numerical divergence of the iterates, which can be caused either by excess noise or outliers. Our sgd package in R offers the most extensive and robust implementation of stochastic gradient descent methods. We demonstrate that sgd dominates alternative software in runtime for several estimation problems with massive data sets. Our applications include the wide class of generalized linear models as well as M-estimation for robust regression.

Analyzing statistical and computational tradeoffs of estimation procedures

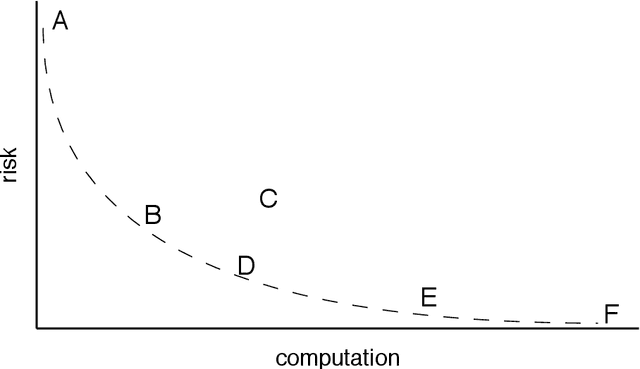
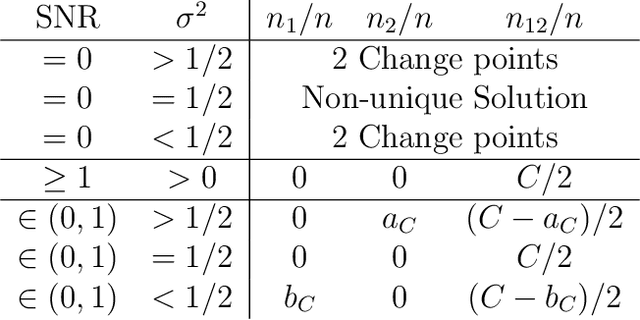
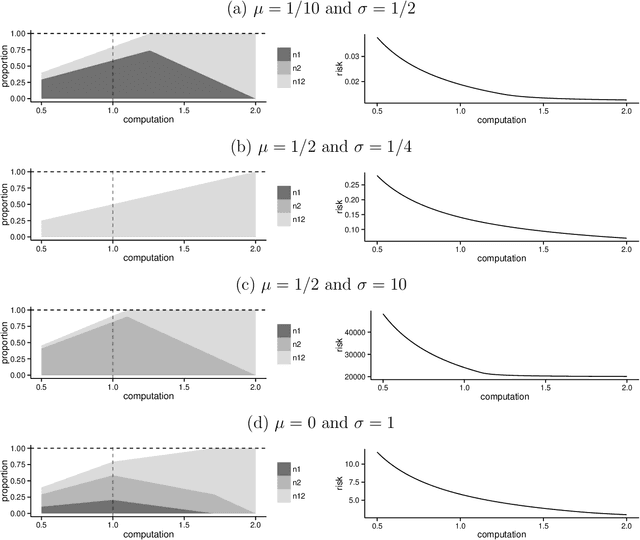
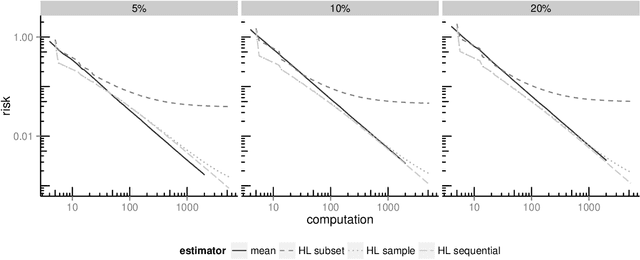
The recent explosion in the amount and dimensionality of data has exacerbated the need of trading off computational and statistical efficiency carefully, so that inference is both tractable and meaningful. We propose a framework that provides an explicit opportunity for practitioners to specify how much statistical risk they are willing to accept for a given computational cost, and leads to a theoretical risk-computation frontier for any given inference problem. We illustrate the tradeoff between risk and computation and illustrate the frontier in three distinct settings. First, we derive analytic forms for the risk of estimating parameters in the classical setting of estimating the mean and variance for normally distributed data and for the more general setting of parameters of an exponential family. The second example concentrates on computationally constrained Hodges-Lehmann estimators. We conclude with an evaluation of risk associated with early termination of iterative matrix inversion algorithms in the context of linear regression.

Geometric Representations of Random Hypergraphs

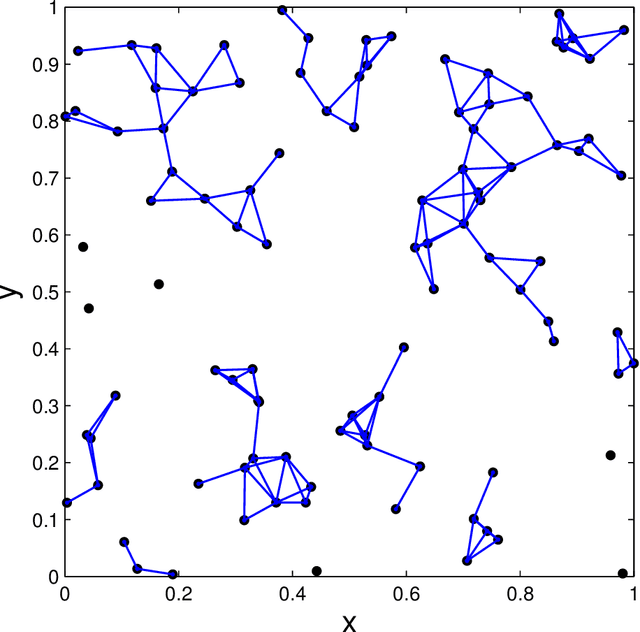
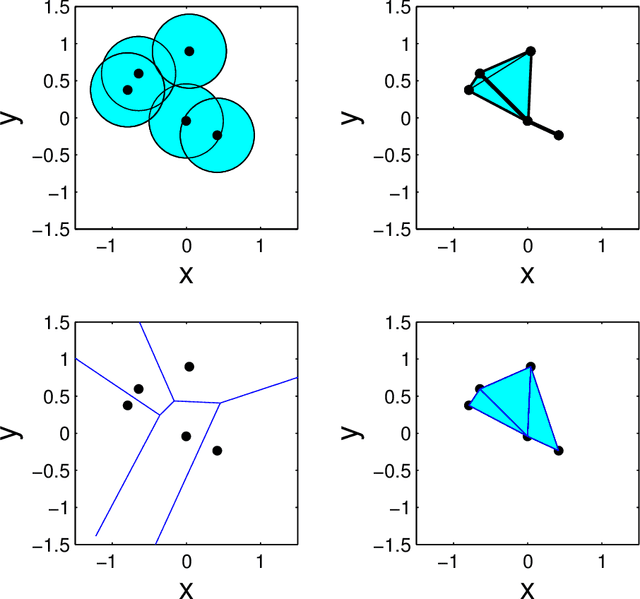
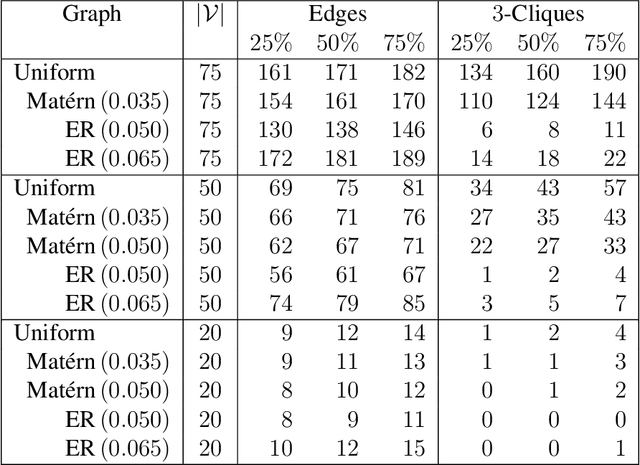
A parametrization of hypergraphs based on the geometry of points in $\mathbf{R}^d$ is developed. Informative prior distributions on hypergraphs are induced through this parametrization by priors on point configurations via spatial processes. This prior specification is used to infer conditional independence models or Markov structure of multivariate distributions. Specifically, we can recover both the junction tree factorization as well as the hyper Markov law. This approach offers greater control on the distribution of graph features than Erd\"os-R\'enyi random graphs, supports inference of factorizations that cannot be retrieved by a graph alone, and leads to new Metropolis\slash Hastings Markov chain Monte Carlo algorithms with both local and global moves in graph space. We illustrate the utility of this parametrization and prior specification using simulations.

Implicit Temporal Differences

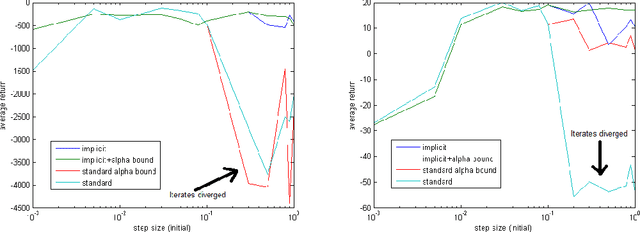
In reinforcement learning, the TD($\lambda$) algorithm is a fundamental policy evaluation method with an efficient online implementation that is suitable for large-scale problems. One practical drawback of TD($\lambda$) is its sensitivity to the choice of the step-size. It is an empirically well-known fact that a large step-size leads to fast convergence, at the cost of higher variance and risk of instability. In this work, we introduce the implicit TD($\lambda$) algorithm which has the same function and computational cost as TD($\lambda$), but is significantly more stable. We provide a theoretical explanation of this stability and an empirical evaluation of implicit TD($\lambda$) on typical benchmark tasks. Our results show that implicit TD($\lambda$) outperforms standard TD($\lambda$) and a state-of-the-art method that automatically tunes the step-size, and thus shows promise for wide applicability.