Aaron Clauset
Meta-learning optimizes predictions of missing links in real-world networks
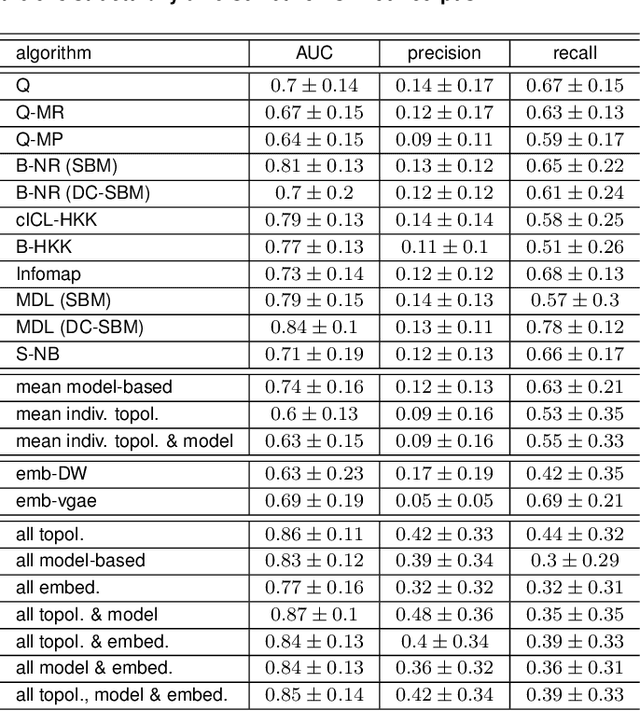
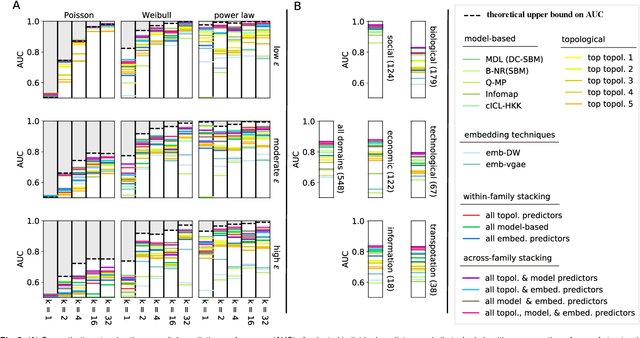
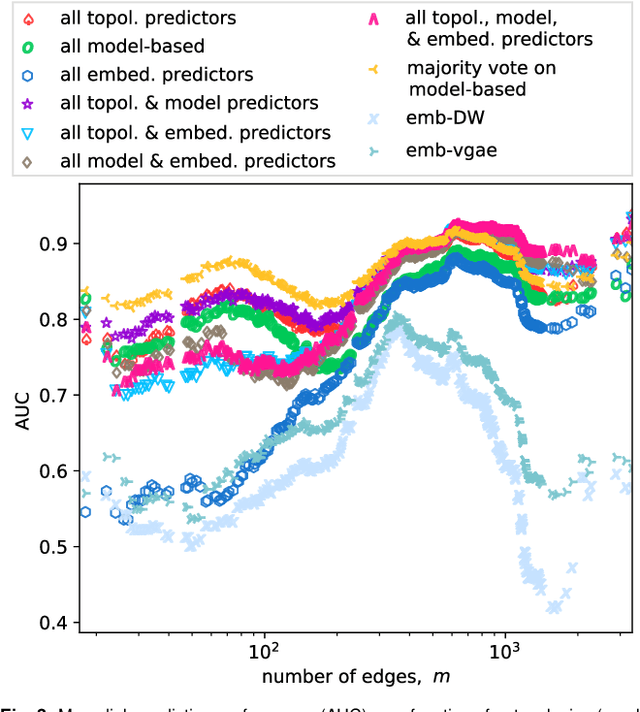
Aug 12, 2025Abstract:Relational data are ubiquitous in real-world data applications, e.g., in social network analysis or biological modeling, but networks are nearly always incompletely observed. The state-of-the-art for predicting missing links in the hard case of a network without node attributes uses model stacking or neural network techniques. It remains unknown which approach is best, and whether or how the best choice of algorithm depends on the input network's characteristics. We answer these questions systematically using a large, structurally diverse benchmark of 550 real-world networks under two standard accuracy measures (AUC and Top-k), comparing four stacking algorithms with 42 topological link predictors, two of which we introduce here, and two graph neural network algorithms. We show that no algorithm is best across all input networks, all algorithms perform well on most social networks, and few perform well on economic and biological networks. Overall, model stacking with a random forest is both highly scalable and surpasses on AUC or is competitive with graph neural networks on Top-k accuracy. But, algorithm performance depends strongly on network characteristics like the degree distribution, triangle density, and degree assortativity. We introduce a meta-learning algorithm that exploits this variability to optimize link predictions for individual networks by selecting the best algorithm to apply, which we show outperforms all state-of-the-art algorithms and scales to large networks.
Stacking Models for Nearly Optimal Link Prediction in Complex Networks
Sep 17, 2019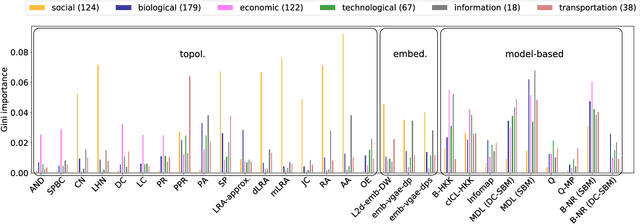
Abstract:Most real-world networks are incompletely observed. Algorithms that can accurately predict which links are missing can dramatically speedup the collection of network data and improve the validity of network models. Many algorithms now exist for predicting missing links, given a partially observed network, but it has remained unknown whether a single best predictor exists, how link predictability varies across methods and networks from different domains, and how close to optimality current methods are. We answer these questions by systematically evaluating 203 individual link predictor algorithms, representing three popular families of methods, applied to a large corpus of 548 structurally diverse networks from six scientific domains. We first show that individual algorithms exhibit a broad diversity of prediction errors, such that no one predictor or family is best, or worst, across all realistic inputs. We then exploit this diversity via meta-learning to construct a series of "stacked" models that combine predictors into a single algorithm. Applied to a broad range of synthetic networks, for which we may analytically calculate optimal performance, these stacked models achieve optimal or nearly optimal levels of accuracy. Applied to real-world networks, stacked models are also superior, but their accuracy varies strongly by domain, suggesting that link prediction may be fundamentally easier in social networks than in biological or technological networks. These results indicate that the state-of-the-art for link prediction comes from combining individual algorithms, which achieves nearly optimal predictions. We close with a brief discussion of limitations and opportunities for further improvement of these results.
Evaluating Overfit and Underfit in Models of Network Community Structure
Mar 01, 2018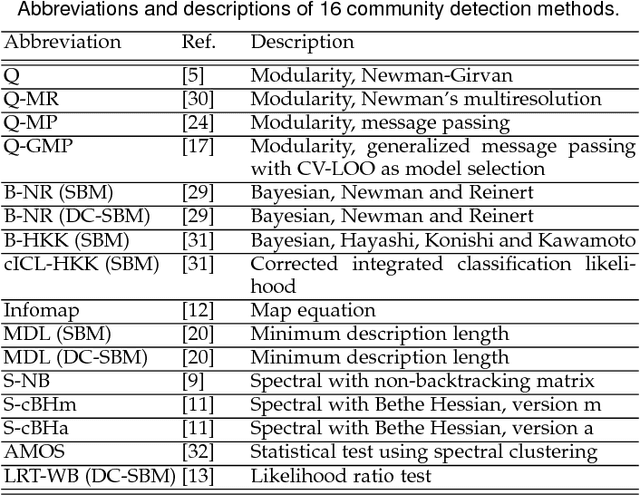
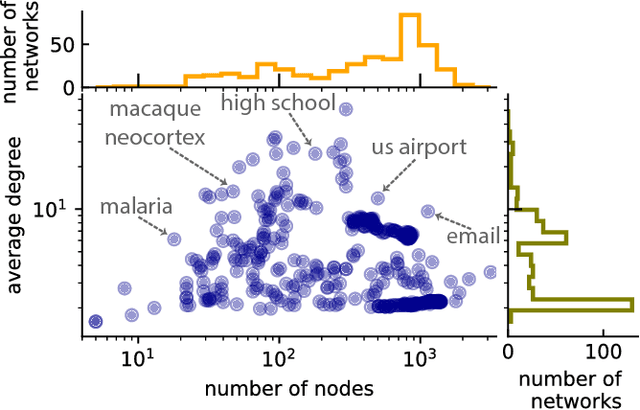
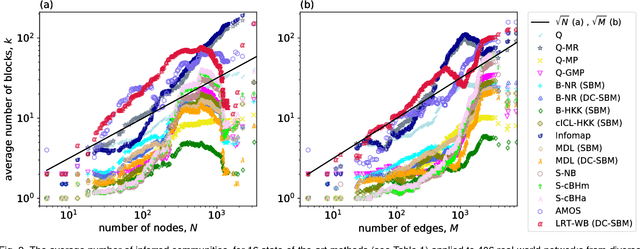
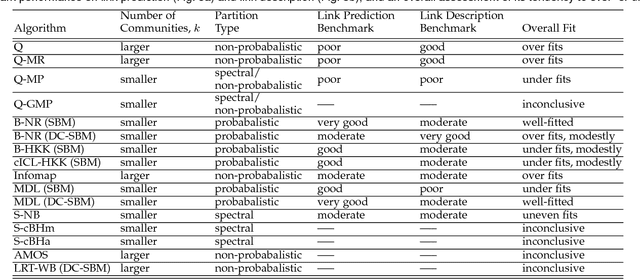
Abstract:A common data mining task on networks is community detection, which seeks an unsupervised decomposition of a network into structural groups based on statistical regularities in the network's connectivity. Although many methods exist, the No Free Lunch theorem for community detection implies that each makes some kind of tradeoff, and no algorithm can be optimal on all inputs. Thus, different algorithms will over or underfit on different inputs, finding more, fewer, or just different communities than is optimal, and evaluation methods that use a metadata partition as a ground truth will produce misleading conclusions about general accuracy. Here, we present a broad evaluation of over and underfitting in community detection, comparing the behavior of 16 state-of-the-art community detection algorithms on a novel and structurally diverse corpus of 406 real-world networks. We find that (i) algorithms vary widely both in the number of communities they find and in their corresponding composition, given the same input, (ii) algorithms can be clustered into distinct high-level groups based on similarities of their outputs on real-world networks, and (iii) these differences induce wide variation in accuracy on link prediction and link description tasks. We introduce a new diagnostic for evaluating overfitting and underfitting in practice, and use it to roughly divide community detection methods into general and specialized learning algorithms. Across methods and inputs, Bayesian techniques based on the stochastic block model and a minimum description length approach to regularization represent the best general learning approach, but can be outperformed under specific circumstances. These results introduce both a theoretically principled approach to evaluate over and underfitting in models of network community structure and a realistic benchmark by which new methods may be evaluated and compared.
Characterizing the structural diversity of complex networks across domains
Oct 31, 2017



Abstract:The structure of complex networks has been of interest in many scientific and engineering disciplines over the decades. A number of studies in the field have been focused on finding the common properties among different kinds of networks such as heavy-tail degree distribution, small-worldness and modular structure and they have tried to establish a theory of structural universality in complex networks. However, there is no comprehensive study of network structure across a diverse set of domains in order to explain the structural diversity we observe in the real-world networks. In this paper, we study 986 real-world networks of diverse domains ranging from ecological food webs to online social networks along with 575 networks generated from four popular network models. Our study utilizes a number of machine learning techniques such as random forest and confusion matrix in order to show the relationships among network domains in terms of network structure. Our results indicate that there are some partitions of network categories in which networks are hard to distinguish based purely on network structure. We have found that these partitions of network categories tend to have similar underlying functions, constraints and/or generative mechanisms of networks even though networks in the same partition have different origins, e.g., biological processes, results of engineering by human being, etc. This suggests that the origin of a network, whether it's biological, technological or social, may not necessarily be a decisive factor of the formation of similar network structure. Our findings shed light on the possible direction along which we could uncover the hidden principles for the structural diversity of complex networks.
The ground truth about metadata and community detection in networks
May 03, 2017Abstract:Across many scientific domains, there is a common need to automatically extract a simplified view or coarse-graining of how a complex system's components interact. This general task is called community detection in networks and is analogous to searching for clusters in independent vector data. It is common to evaluate the performance of community detection algorithms by their ability to find so-called "ground truth" communities. This works well in synthetic networks with planted communities because such networks' links are formed explicitly based on those known communities. However, there are no planted communities in real world networks. Instead, it is standard practice to treat some observed discrete-valued node attributes, or metadata, as ground truth. Here, we show that metadata are not the same as ground truth, and that treating them as such induces severe theoretical and practical problems. We prove that no algorithm can uniquely solve community detection, and we prove a general No Free Lunch theorem for community detection, which implies that there can be no algorithm that is optimal for all possible community detection tasks. However, community detection remains a powerful tool and node metadata still have value so a careful exploration of their relationship with network structure can yield insights of genuine worth. We illustrate this point by introducing two statistical techniques that can quantify the relationship between metadata and community structure for a broad class of models. We demonstrate these techniques using both synthetic and real-world networks, and for multiple types of metadata and community structure.
* 27 pages, 10 figures, 11 tables
Structure and inference in annotated networks
Jul 14, 2015



Abstract:For many networks of scientific interest we know both the connections of the network and information about the network nodes, such as the age or gender of individuals in a social network, geographic location of nodes in the Internet, or cellular function of nodes in a gene regulatory network. Here we demonstrate how this "metadata" can be used to improve our analysis and understanding of network structure. We focus in particular on the problem of community detection in networks and develop a mathematically principled approach that combines a network and its metadata to detect communities more accurately than can be done with either alone. Crucially, the method does not assume that the metadata are correlated with the communities we are trying to find. Instead the method learns whether a correlation exists and correctly uses or ignores the metadata depending on whether they contain useful information. The learned correlations are also of interest in their own right, allowing us to make predictions about the community membership of nodes whose network connections are unknown. We demonstrate our method on synthetic networks with known structure and on real-world networks, large and small, drawn from social, biological, and technological domains.
* 16 pages, 7 figures, 1 table
Detectability thresholds and optimal algorithms for community structure in dynamic networks
Jun 19, 2015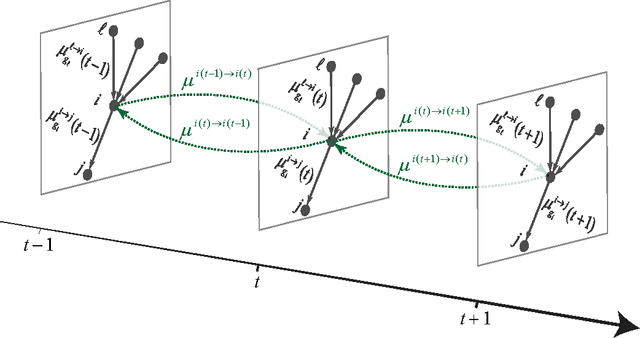
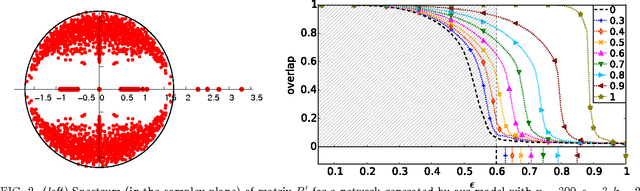
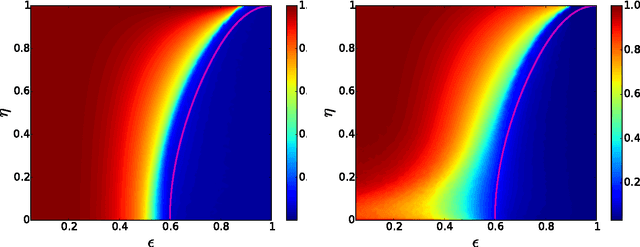
Abstract:We study the fundamental limits on learning latent community structure in dynamic networks. Specifically, we study dynamic stochastic block models where nodes change their community membership over time, but where edges are generated independently at each time step. In this setting (which is a special case of several existing models), we are able to derive the detectability threshold exactly, as a function of the rate of change and the strength of the communities. Below this threshold, we claim that no algorithm can identify the communities better than chance. We then give two algorithms that are optimal in the sense that they succeed all the way down to this limit. The first uses belief propagation (BP), which gives asymptotically optimal accuracy, and the second is a fast spectral clustering algorithm, based on linearizing the BP equations. We verify our analytic and algorithmic results via numerical simulation, and close with a brief discussion of extensions and open questions.
* 9 pages, 3 figures
A unified view of generative models for networks: models, methods, opportunities, and challenges
Nov 14, 2014Abstract:Research on probabilistic models of networks now spans a wide variety of fields, including physics, sociology, biology, statistics, and machine learning. These efforts have produced a diverse ecology of models and methods. Despite this diversity, many of these models share a common underlying structure: pairwise interactions (edges) are generated with probability conditional on latent vertex attributes. Differences between models generally stem from different philosophical choices about how to learn from data or different empirically-motivated goals. The highly interdisciplinary nature of work on these generative models, however, has inhibited the development of a unified view of their similarities and differences. For instance, novel theoretical models and optimization techniques developed in machine learning are largely unknown within the social and biological sciences, which have instead emphasized model interpretability. Here, we describe a unified view of generative models for networks that draws together many of these disparate threads and highlights the fundamental similarities and differences that span these fields. We then describe a number of opportunities and challenges for future work that are revealed by this view.
Detecting change points in the large-scale structure of evolving networks
Nov 14, 2014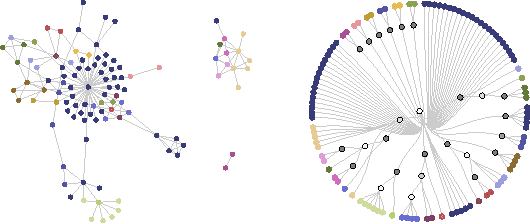
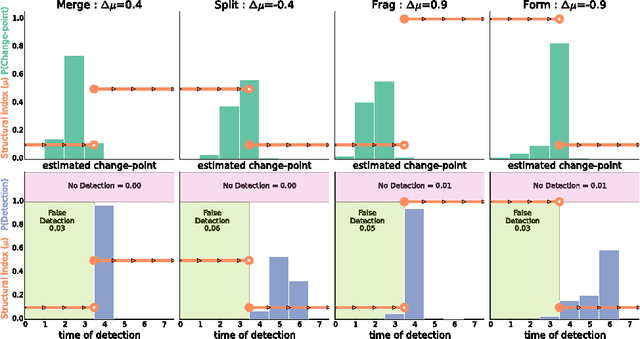
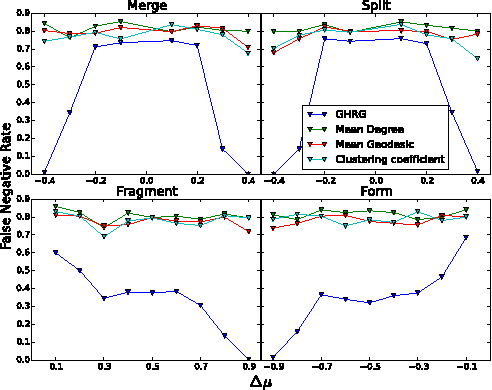
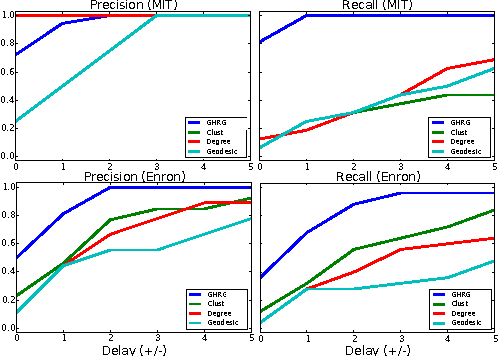
Abstract:Interactions among people or objects are often dynamic in nature and can be represented as a sequence of networks, each providing a snapshot of the interactions over a brief period of time. An important task in analyzing such evolving networks is change-point detection, in which we both identify the times at which the large-scale pattern of interactions changes fundamentally and quantify how large and what kind of change occurred. Here, we formalize for the first time the network change-point detection problem within an online probabilistic learning framework and introduce a method that can reliably solve it. This method combines a generalized hierarchical random graph model with a Bayesian hypothesis test to quantitatively determine if, when, and precisely how a change point has occurred. We analyze the detectability of our method using synthetic data with known change points of different types and magnitudes, and show that this method is more accurate than several previously used alternatives. Applied to two high-resolution evolving social networks, this method identifies a sequence of change points that align with known external "shocks" to these networks.
Efficiently inferring community structure in bipartite networks
Jul 10, 2014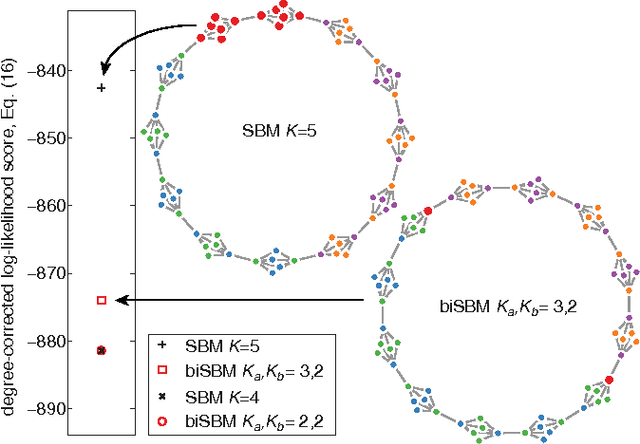
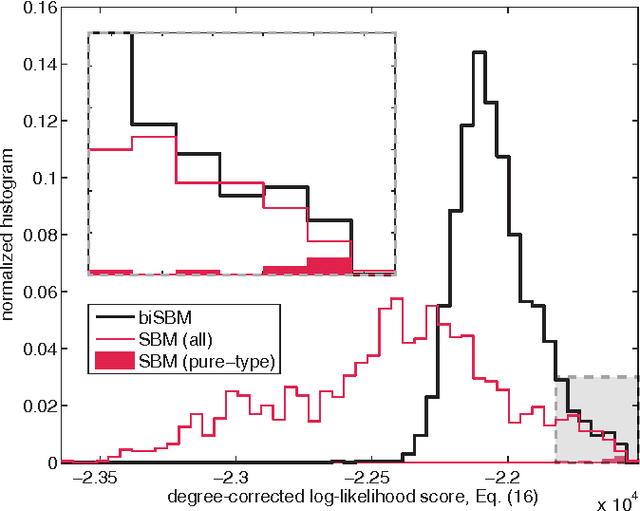
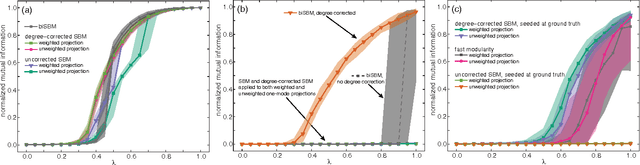
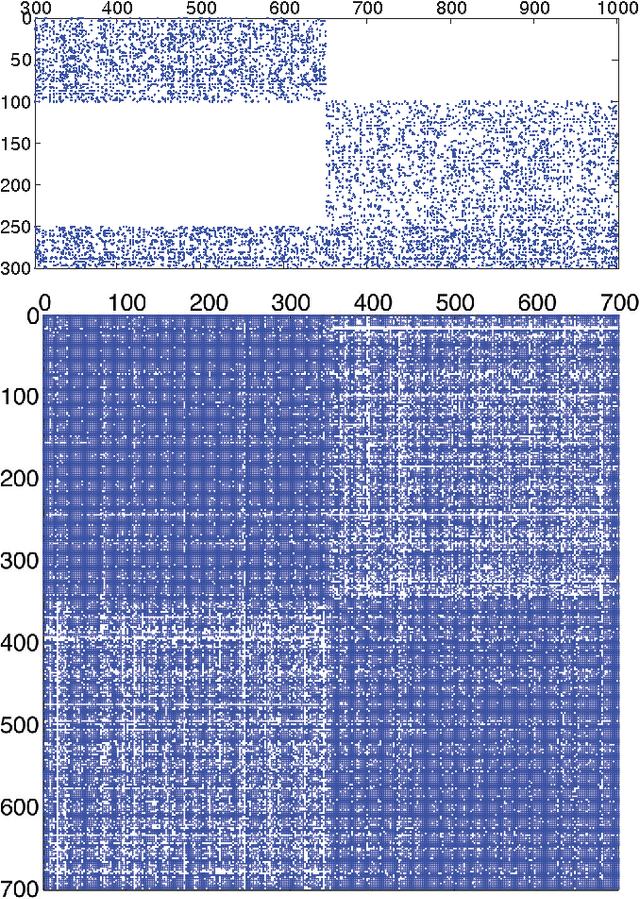
Abstract:Bipartite networks are a common type of network data in which there are two types of vertices, and only vertices of different types can be connected. While bipartite networks exhibit community structure like their unipartite counterparts, existing approaches to bipartite community detection have drawbacks, including implicit parameter choices, loss of information through one-mode projections, and lack of interpretability. Here we solve the community detection problem for bipartite networks by formulating a bipartite stochastic block model, which explicitly includes vertex type information and may be trivially extended to $k$-partite networks. This bipartite stochastic block model yields a projection-free and statistically principled method for community detection that makes clear assumptions and parameter choices and yields interpretable results. We demonstrate this model's ability to efficiently and accurately find community structure in synthetic bipartite networks with known structure and in real-world bipartite networks with unknown structure, and we characterize its performance in practical contexts.
* 12 pages, 9 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge