Machine Unlearning Doesn't Do What You Think: Lessons for Generative AI Policy, Research, and Practice

We articulate fundamental mismatches between technical methods for machine unlearning in Generative AI, and documented aspirations for broader impact that these methods could have for law and policy. These aspirations are both numerous and varied, motivated by issues that pertain to privacy, copyright, safety, and more. For example, unlearning is often invoked as a solution for removing the effects of targeted information from a generative-AI model's parameters, e.g., a particular individual's personal data or in-copyright expression of Spiderman that was included in the model's training data. Unlearning is also proposed as a way to prevent a model from generating targeted types of information in its outputs, e.g., generations that closely resemble a particular individual's data or reflect the concept of "Spiderman." Both of these goals--the targeted removal of information from a model and the targeted suppression of information from a model's outputs--present various technical and substantive challenges. We provide a framework for thinking rigorously about these challenges, which enables us to be clear about why unlearning is not a general-purpose solution for circumscribing generative-AI model behavior in service of broader positive impact. We aim for conceptual clarity and to encourage more thoughtful communication among machine learning (ML), law, and policy experts who seek to develop and apply technical methods for compliance with policy objectives.

The Cadaver in the Machine: The Social Practices of Measurement and Validation in Motion Capture Technology

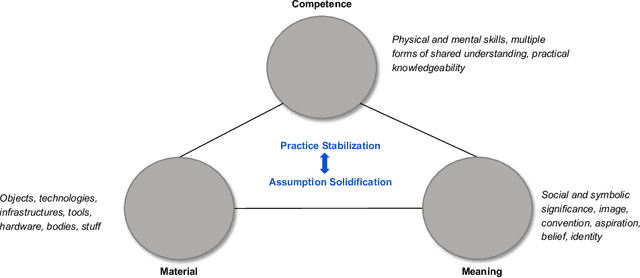
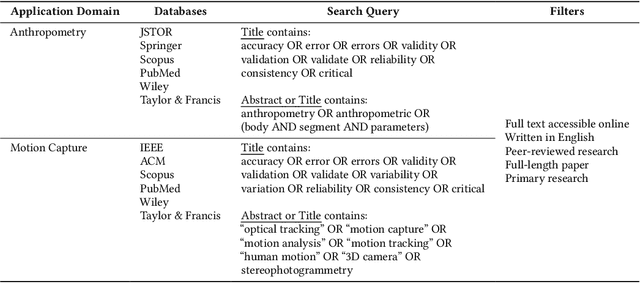
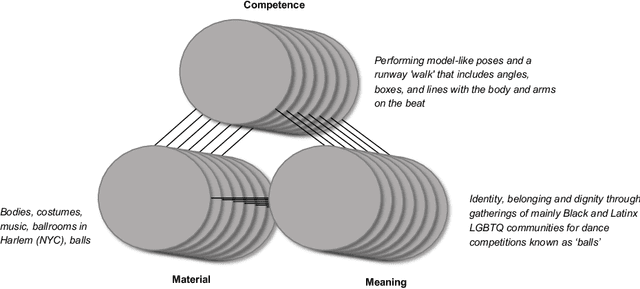
Motion capture systems, used across various domains, make body representations concrete through technical processes. We argue that the measurement of bodies and the validation of measurements for motion capture systems can be understood as social practices. By analyzing the findings of a systematic literature review (N=278) through the lens of social practice theory, we show how these practices, and their varying attention to errors, become ingrained in motion capture design and innovation over time. Moreover, we show how contemporary motion capture systems perpetuate assumptions about human bodies and their movements. We suggest that social practices of measurement and validation are ubiquitous in the development of data- and sensor-driven systems more broadly, and provide this work as a basis for investigating hidden design assumptions and their potential negative consequences in human-computer interaction.

The Role of Relevance in Fair Ranking

Online platforms mediate access to opportunity: relevance-based rankings create and constrain options by allocating exposure to job openings and job candidates in hiring platforms, or sellers in a marketplace. In order to do so responsibly, these socially consequential systems employ various fairness measures and interventions, many of which seek to allocate exposure based on worthiness. Because these constructs are typically not directly observable, platforms must instead resort to using proxy scores such as relevance and infer them from behavioral signals such as searcher clicks. Yet, it remains an open question whether relevance fulfills its role as such a worthiness score in high-stakes fair rankings. In this paper, we combine perspectives and tools from the social sciences, information retrieval, and fairness in machine learning to derive a set of desired criteria that relevance scores should satisfy in order to meaningfully guide fairness interventions. We then empirically show that not all of these criteria are met in a case study of relevance inferred from biased user click data. We assess the impact of these violations on the estimated system fairness and analyze whether existing fairness interventions may mitigate the identified issues. Our analyses and results surface the pressing need for new approaches to relevance collection and generation that are suitable for use in fair ranking.

Measurement and Fairness

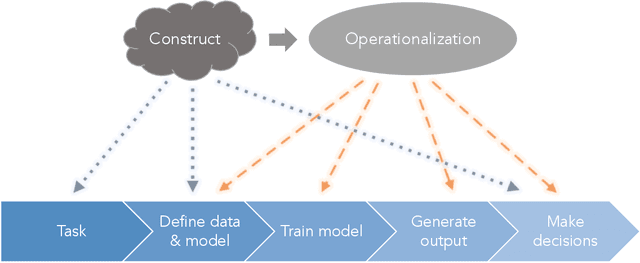
We introduce the language of measurement modeling from the quantitative social sciences as a framework for understanding fairness in computational systems. Computational systems often involve unobservable theoretical constructs, such as "creditworthiness," "teacher quality," or "risk to society," that cannot be measured directly and must instead be inferred from observable properties thought to be related to them---i.e., operationalized via a measurement model. This process introduces the potential for mismatch between the theoretical understanding of the construct purported to be measured and its operationalization. Indeed, we argue that many of the harms discussed in the literature on fairness in computational systems are direct results of such mismatches. Further complicating these discussions is the fact that fairness itself is an unobservable theoretical construct. Moreover, it is an essentially contested construct---i.e., it has many different theoretical understandings depending on the context. We argue that this contestedness underlies recent debates about fairness definitions: disagreements that appear to be about contradictory operationalizations are, in fact, disagreements about different theoretical understandings of the construct itself. By introducing the language of measurement modeling, we provide the computer science community with a process for making explicit and testing assumptions about unobservable theoretical constructs, thereby making it easier to identify, characterize, and even mitigate fairness-related harms.

Discovering heterogeneous subpopulations for fine-grained analysis of opioid use and opioid use disorders

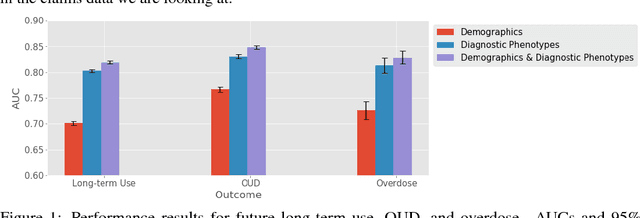
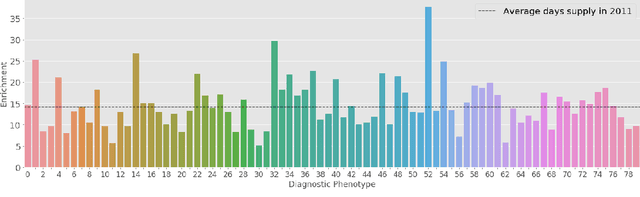
The opioid epidemic in the United States claims over 40,000 lives per year, and it is estimated that well over two million Americans have an opioid use disorder. Over-prescription and misuse of prescription opioids play an important role in the epidemic. Individuals who are prescribed opioids, and who are diagnosed with opioid use disorder, have diverse underlying health states. Policy interventions targeting prescription opioid use, opioid use disorder, and overdose often fail to account for this variation. To identify latent health states, or phenotypes, pertinent to opioid use and opioid use disorders, we use probabilistic topic modeling with medical diagnosis histories from a statewide population of individuals who were prescribed opioids. We demonstrate that our learned phenotypes are predictive of future opioid use-related outcomes. In addition, we show how the learned phenotypes can provide important context for variability in opioid prescriptions. Understanding the heterogeneity in individual health states and in prescription opioid use can help identify policy interventions to address this public health crisis.

A unified view of generative models for networks: models, methods, opportunities, and challenges

Research on probabilistic models of networks now spans a wide variety of fields, including physics, sociology, biology, statistics, and machine learning. These efforts have produced a diverse ecology of models and methods. Despite this diversity, many of these models share a common underlying structure: pairwise interactions (edges) are generated with probability conditional on latent vertex attributes. Differences between models generally stem from different philosophical choices about how to learn from data or different empirically-motivated goals. The highly interdisciplinary nature of work on these generative models, however, has inhibited the development of a unified view of their similarities and differences. For instance, novel theoretical models and optimization techniques developed in machine learning are largely unknown within the social and biological sciences, which have instead emphasized model interpretability. Here, we describe a unified view of generative models for networks that draws together many of these disparate threads and highlights the fundamental similarities and differences that span these fields. We then describe a number of opportunities and challenges for future work that are revealed by this view.

Efficiently inferring community structure in bipartite networks

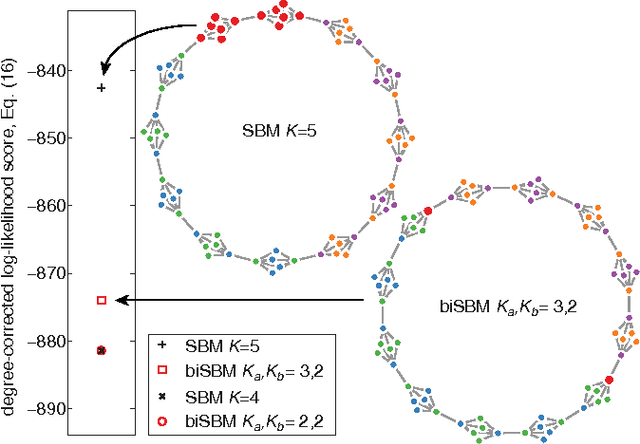
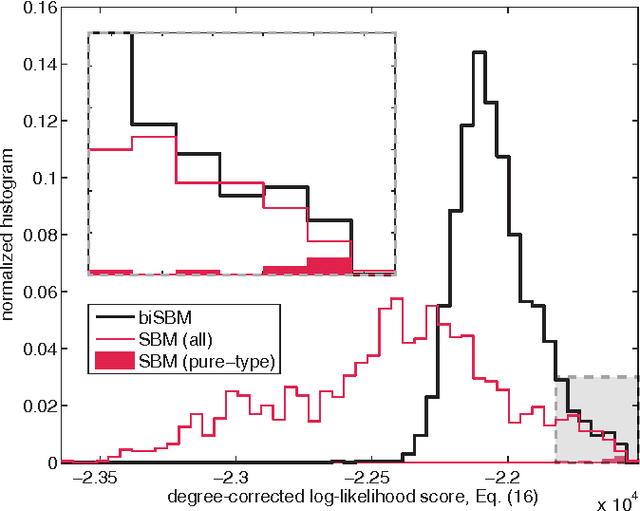
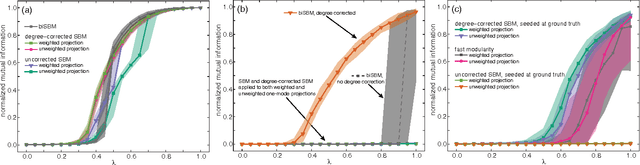
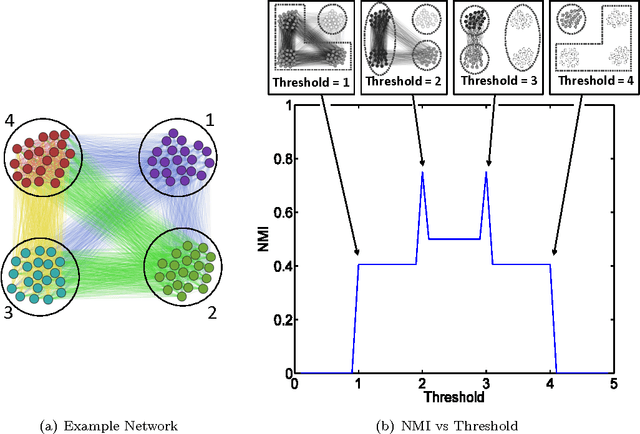
Bipartite networks are a common type of network data in which there are two types of vertices, and only vertices of different types can be connected. While bipartite networks exhibit community structure like their unipartite counterparts, existing approaches to bipartite community detection have drawbacks, including implicit parameter choices, loss of information through one-mode projections, and lack of interpretability. Here we solve the community detection problem for bipartite networks by formulating a bipartite stochastic block model, which explicitly includes vertex type information and may be trivially extended to $k$-partite networks. This bipartite stochastic block model yields a projection-free and statistically principled method for community detection that makes clear assumptions and parameter choices and yields interpretable results. We demonstrate this model's ability to efficiently and accurately find community structure in synthetic bipartite networks with known structure and in real-world bipartite networks with unknown structure, and we characterize its performance in practical contexts.

Learning Latent Block Structure in Weighted Networks

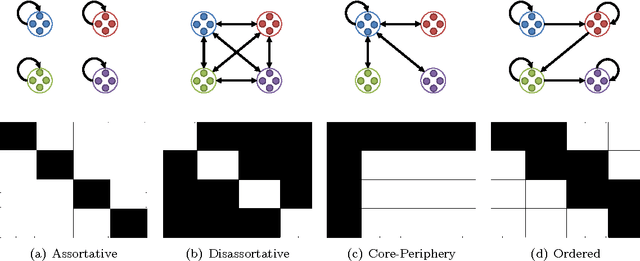
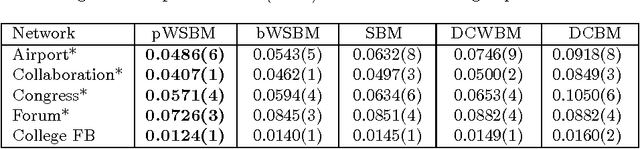
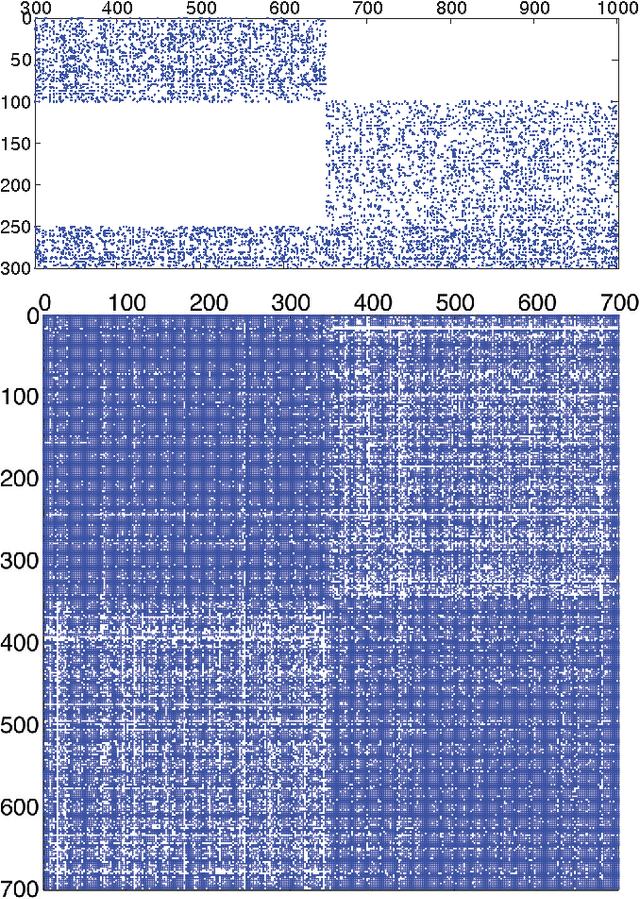
Community detection is an important task in network analysis, in which we aim to learn a network partition that groups together vertices with similar community-level connectivity patterns. By finding such groups of vertices with similar structural roles, we extract a compact representation of the network's large-scale structure, which can facilitate its scientific interpretation and the prediction of unknown or future interactions. Popular approaches, including the stochastic block model, assume edges are unweighted, which limits their utility by throwing away potentially useful information. We introduce the `weighted stochastic block model' (WSBM), which generalizes the stochastic block model to networks with edge weights drawn from any exponential family distribution. This model learns from both the presence and weight of edges, allowing it to discover structure that would otherwise be hidden when weights are discarded or thresholded. We describe a Bayesian variational algorithm for efficiently approximating this model's posterior distribution over latent block structures. We then evaluate the WSBM's performance on both edge-existence and edge-weight prediction tasks for a set of real-world weighted networks. In all cases, the WSBM performs as well or better than the best alternatives on these tasks.

Adapting the Stochastic Block Model to Edge-Weighted Networks

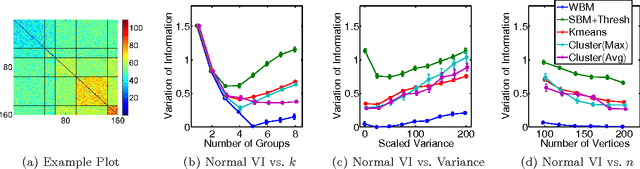
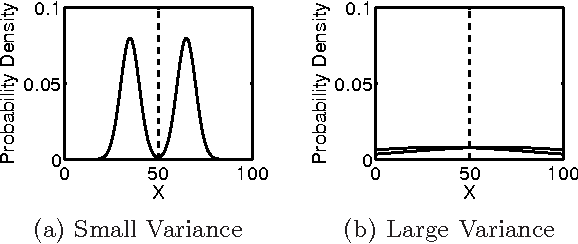
We generalize the stochastic block model to the important case in which edges are annotated with weights drawn from an exponential family distribution. This generalization introduces several technical difficulties for model estimation, which we solve using a Bayesian approach. We introduce a variational algorithm that efficiently approximates the model's posterior distribution for dense graphs. In specific numerical experiments on edge-weighted networks, this weighted stochastic block model outperforms the common approach of first applying a single threshold to all weights and then applying the classic stochastic block model, which can obscure latent block structure in networks. This model will enable the recovery of latent structure in a broader range of network data than was previously possible.

Adapting to Non-stationarity with Growing Expert Ensembles

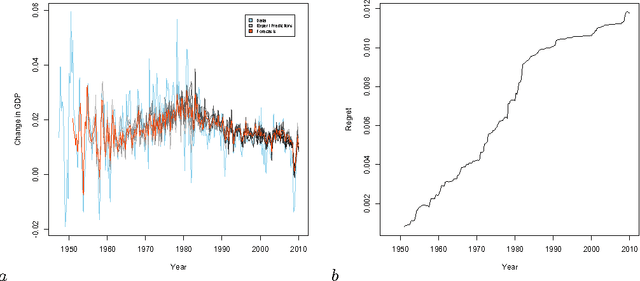
When dealing with time series with complex non-stationarities, low retrospective regret on individual realizations is a more appropriate goal than low prospective risk in expectation. Online learning algorithms provide powerful guarantees of this form, and have often been proposed for use with non-stationary processes because of their ability to switch between different forecasters or ``experts''. However, existing methods assume that the set of experts whose forecasts are to be combined are all given at the start, which is not plausible when dealing with a genuinely historical or evolutionary system. We show how to modify the ``fixed shares'' algorithm for tracking the best expert to cope with a steadily growing set of experts, obtained by fitting new models to new data as it becomes available, and obtain regret bounds for the growing ensemble.