Adaptively Truncating Backpropagation Through Time to Control Gradient Bias

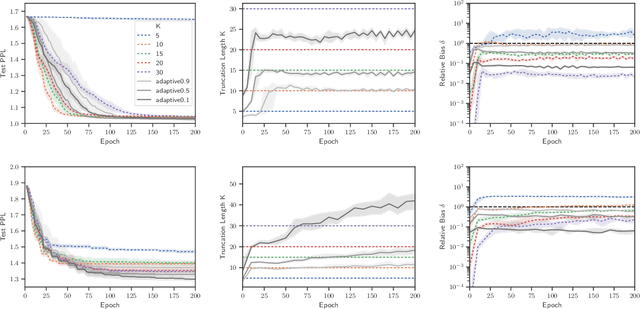
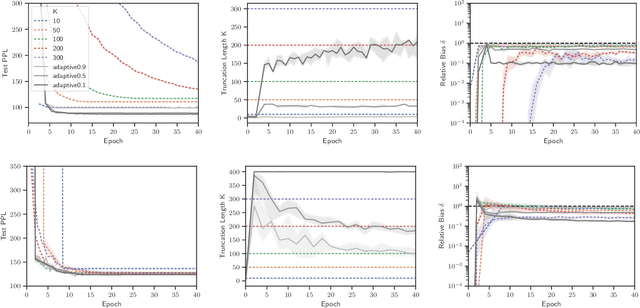
Truncated backpropagation through time (TBPTT) is a popular method for learning in recurrent neural networks (RNNs) that saves computation and memory at the cost of bias by truncating backpropagation after a fixed number of lags. In practice, choosing the optimal truncation length is difficult: TBPTT will not converge if the truncation length is too small, or will converge slowly if it is too large. We propose an adaptive TBPTT scheme that converts the problem from choosing a temporal lag to one of choosing a tolerable amount of gradient bias. For many realistic RNNs, the TBPTT gradients decay geometrically for large lags; under this condition, we can control the bias by varying the truncation length adaptively. For RNNs with smooth activation functions, we prove that this bias controls the convergence rate of SGD with biased gradients for our non-convex loss. Using this theory, we develop a practical method for adaptively estimating the truncation length during training. We evaluate our adaptive TBPTT method on synthetic data and language modeling tasks and find that our adaptive TBPTT ameliorates the computational pitfalls of fixed TBPTT.

Stochastic Gradient MCMC for Nonlinear State Space Models

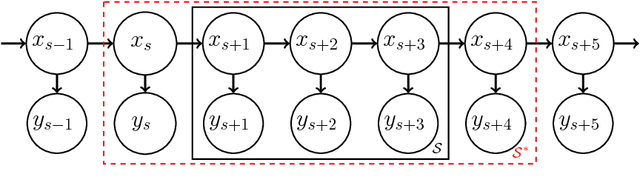
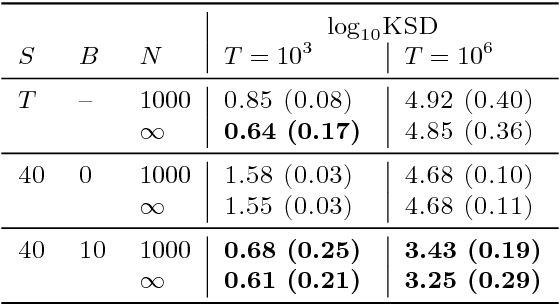
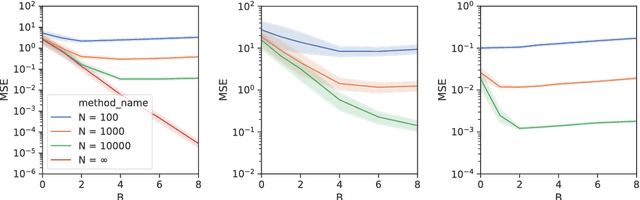
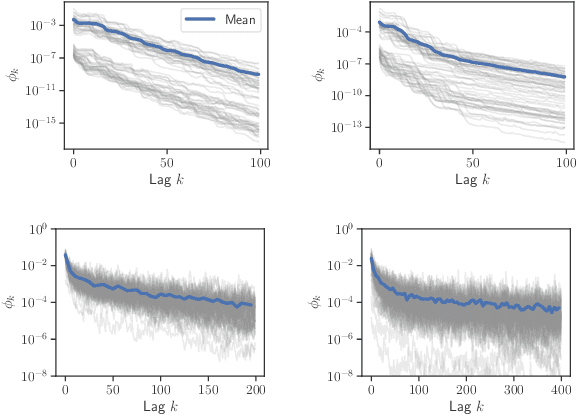
State space models (SSMs) provide a flexible framework for modeling complex time series via a latent stochastic process. Inference for nonlinear, non-Gaussian SSMs is often tackled with particle methods that do not scale well to long time series. The challenge is two-fold: not only do computations scale linearly with time, as in the linear case, but particle filters additionally suffer from increasing particle degeneracy with longer series. Stochastic gradient MCMC methods have been developed to scale inference for hidden Markov models (HMMs) and linear SSMs using buffered stochastic gradient estimates to account for temporal dependencies. We extend these stochastic gradient estimators to nonlinear SSMs using particle methods. We present error bounds that account for both buffering error and particle error in the case of nonlinear SSMs that are log-concave in the latent process. We evaluate our proposed particle buffered stochastic gradient using SGMCMC for inference on both long sequential synthetic and minute-resolution financial returns data, demonstrating the importance of this class of methods.

Stochastic Gradient MCMC for State Space Models

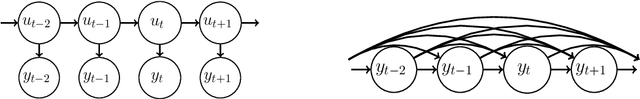
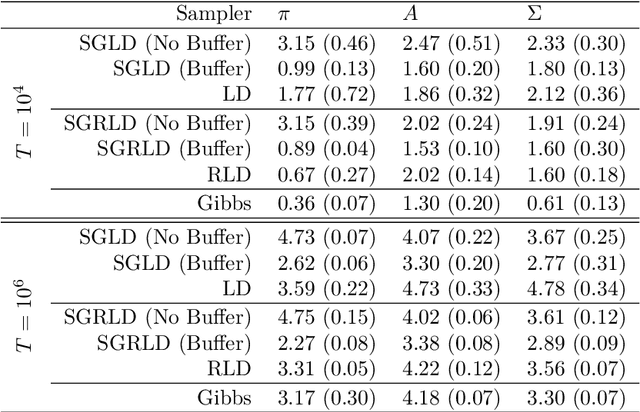
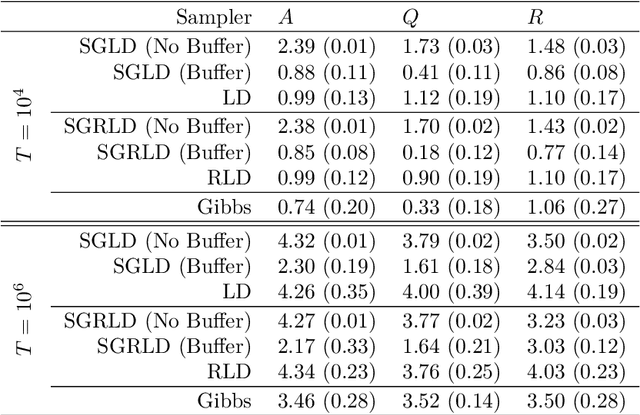
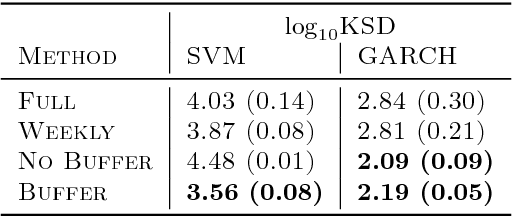
State space models (SSMs) are a flexible approach to modeling complex time series. However, inference in SSMs is often computationally prohibitive for long time series. Stochastic gradient MCMC (SGMCMC) is a popular method for scalable Bayesian inference for large independent data. Unfortunately when applied to dependent data, such as in SSMs, SGMCMC's stochastic gradient estimates are biased as they break crucial temporal dependencies. To alleviate this, we propose stochastic gradient estimators that control this bias by performing additional computation in a `buffer' to reduce breaking dependencies. Furthermore, we derive error bounds for this bias and show a geometric decay under mild conditions. Using these estimators, we develop novel SGMCMC samplers for discrete, continuous and mixed-type SSMs. Our experiments on real and synthetic data demonstrate the effectiveness of our SGMCMC algorithms compared to batch MCMC, allowing us to scale inference to long time series with millions of time points.

Approximate Collapsed Gibbs Clustering with Expectation Propagation

We develop a framework for approximating collapsed Gibbs sampling in generative latent variable cluster models. Collapsed Gibbs is a popular MCMC method, which integrates out variables in the posterior to improve mixing. Unfortunately for many complex models, integrating out these variables is either analytically or computationally intractable. We efficiently approximate the necessary collapsed Gibbs integrals by borrowing ideas from expectation propagation. We present two case studies where exact collapsed Gibbs sampling is intractable: mixtures of Student-t's and time series clustering. Our experiments on real and synthetic data show that our approximate sampler enables a runtime-accuracy tradeoff in sampling these types of models, providing results with competitive accuracy much more rapidly than the naive Gibbs samplers one would otherwise rely on in these scenarios.

Learning Latent Block Structure in Weighted Networks

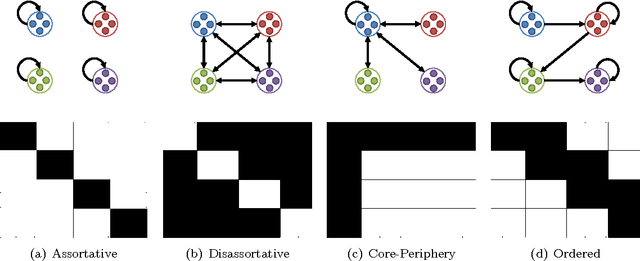
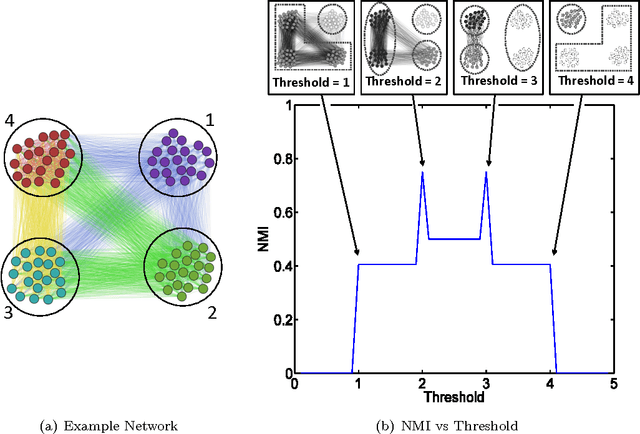
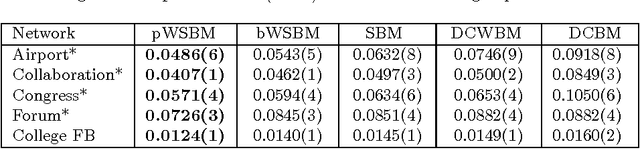
Community detection is an important task in network analysis, in which we aim to learn a network partition that groups together vertices with similar community-level connectivity patterns. By finding such groups of vertices with similar structural roles, we extract a compact representation of the network's large-scale structure, which can facilitate its scientific interpretation and the prediction of unknown or future interactions. Popular approaches, including the stochastic block model, assume edges are unweighted, which limits their utility by throwing away potentially useful information. We introduce the `weighted stochastic block model' (WSBM), which generalizes the stochastic block model to networks with edge weights drawn from any exponential family distribution. This model learns from both the presence and weight of edges, allowing it to discover structure that would otherwise be hidden when weights are discarded or thresholded. We describe a Bayesian variational algorithm for efficiently approximating this model's posterior distribution over latent block structures. We then evaluate the WSBM's performance on both edge-existence and edge-weight prediction tasks for a set of real-world weighted networks. In all cases, the WSBM performs as well or better than the best alternatives on these tasks.

Adapting the Stochastic Block Model to Edge-Weighted Networks

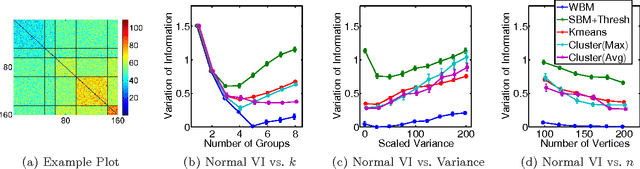
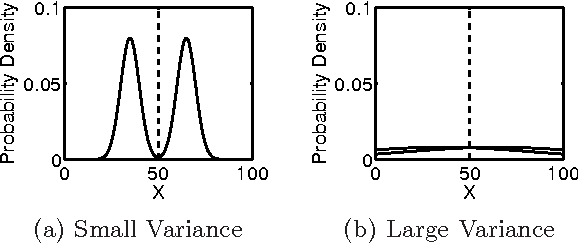
We generalize the stochastic block model to the important case in which edges are annotated with weights drawn from an exponential family distribution. This generalization introduces several technical difficulties for model estimation, which we solve using a Bayesian approach. We introduce a variational algorithm that efficiently approximates the model's posterior distribution for dense graphs. In specific numerical experiments on edge-weighted networks, this weighted stochastic block model outperforms the common approach of first applying a single threshold to all weights and then applying the classic stochastic block model, which can obscure latent block structure in networks. This model will enable the recovery of latent structure in a broader range of network data than was previously possible.