Preferential Subsampling for Stochastic Gradient Langevin Dynamics

Stochastic gradient MCMC (SGMCMC) offers a scalable alternative to traditional MCMC, by constructing an unbiased estimate of the gradient of the log-posterior with a small, uniformly-weighted subsample of the data. While efficient to compute, the resulting gradient estimator may exhibit a high variance and impact sampler performance. The problem of variance control has been traditionally addressed by constructing a better stochastic gradient estimator, often using control variates. We propose to use a discrete, non-uniform probability distribution to preferentially subsample data points that have a greater impact on the stochastic gradient. In addition, we present a method of adaptively adjusting the subsample size at each iteration of the algorithm, so that we increase the subsample size in areas of the sample space where the gradient is harder to estimate. We demonstrate that such an approach can maintain the same level of accuracy while substantially reducing the average subsample size that is used.

Stochastic Gradient MCMC for Nonlinear State Space Models

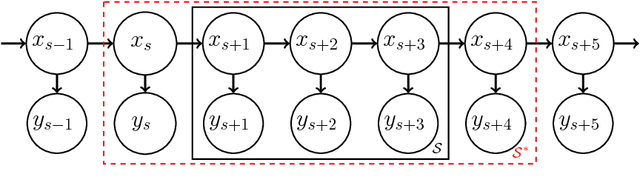
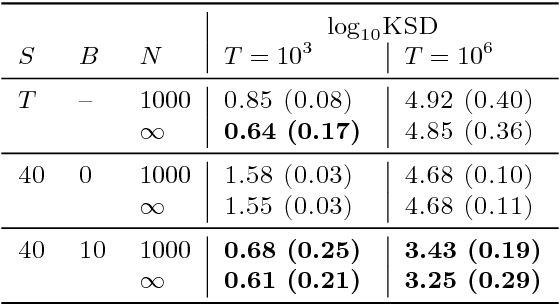
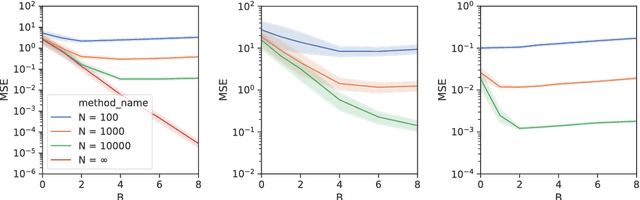
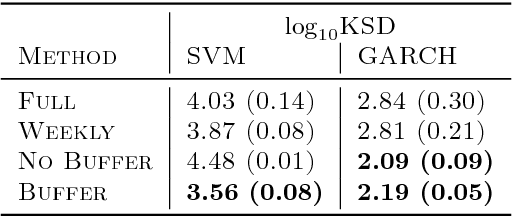
State space models (SSMs) provide a flexible framework for modeling complex time series via a latent stochastic process. Inference for nonlinear, non-Gaussian SSMs is often tackled with particle methods that do not scale well to long time series. The challenge is two-fold: not only do computations scale linearly with time, as in the linear case, but particle filters additionally suffer from increasing particle degeneracy with longer series. Stochastic gradient MCMC methods have been developed to scale inference for hidden Markov models (HMMs) and linear SSMs using buffered stochastic gradient estimates to account for temporal dependencies. We extend these stochastic gradient estimators to nonlinear SSMs using particle methods. We present error bounds that account for both buffering error and particle error in the case of nonlinear SSMs that are log-concave in the latent process. We evaluate our proposed particle buffered stochastic gradient using SGMCMC for inference on both long sequential synthetic and minute-resolution financial returns data, demonstrating the importance of this class of methods.