Scalable Monte Carlo for Bayesian Learning

This book aims to provide a graduate-level introduction to advanced topics in Markov chain Monte Carlo (MCMC) algorithms, as applied broadly in the Bayesian computational context. Most, if not all of these topics (stochastic gradient MCMC, non-reversible MCMC, continuous time MCMC, and new techniques for convergence assessment) have emerged as recently as the last decade, and have driven substantial recent practical and theoretical advances in the field. A particular focus is on methods that are scalable with respect to either the amount of data, or the data dimension, motivated by the emerging high-priority application areas in machine learning and AI.

Stochastic Gradient Piecewise Deterministic Monte Carlo Samplers

Recent work has suggested using Monte Carlo methods based on piecewise deterministic Markov processes (PDMPs) to sample from target distributions of interest. PDMPs are non-reversible continuous-time processes endowed with momentum, and hence can mix better than standard reversible MCMC samplers. Furthermore, they can incorporate exact sub-sampling schemes which only require access to a single (randomly selected) data point at each iteration, yet without introducing bias to the algorithm's stationary distribution. However, the range of models for which PDMPs can be used, particularly with sub-sampling, is limited. We propose approximate simulation of PDMPs with sub-sampling for scalable sampling from posterior distributions. The approximation takes the form of an Euler approximation to the true PDMP dynamics, and involves using an estimate of the gradient of the log-posterior based on a data sub-sample. We thus call this class of algorithms stochastic-gradient PDMPs. Importantly, the trajectories of stochastic-gradient PDMPs are continuous and can leverage recent ideas for sampling from measures with continuous and atomic components. We show these methods are easy to implement, present results on their approximation error and demonstrate numerically that this class of algorithms has similar efficiency to, but is more robust than, stochastic gradient Langevin dynamics.

A Constant-per-Iteration Likelihood Ratio Test for Online Changepoint Detection for Exponential Family Models

Online changepoint detection algorithms that are based on likelihood-ratio tests have been shown to have excellent statistical properties. However, a simple online implementation is computationally infeasible as, at time $T$, it involves considering $O(T)$ possible locations for the change. Recently, the FOCuS algorithm has been introduced for detecting changes in mean in Gaussian data that decreases the per-iteration cost to $O(\log T)$. This is possible by using pruning ideas, which reduce the set of changepoint locations that need to be considered at time $T$ to approximately $\log T$. We show that if one wishes to perform the likelihood ratio test for a different one-parameter exponential family model, then exactly the same pruning rule can be used, and again one need only consider approximately $\log T$ locations at iteration $T$. Furthermore, we show how we can adaptively perform the maximisation step of the algorithm so that we need only maximise the test statistic over a small subset of these possible locations. Empirical results show that the resulting online algorithm, which can detect changes under a wide range of models, has a constant-per-iteration cost on average.

A Log-Linear Non-Parametric Online Changepoint Detection Algorithm based on Functional Pruning

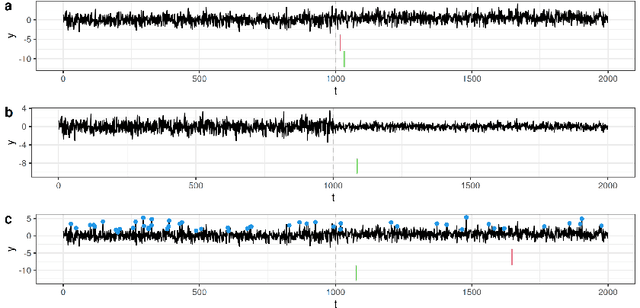
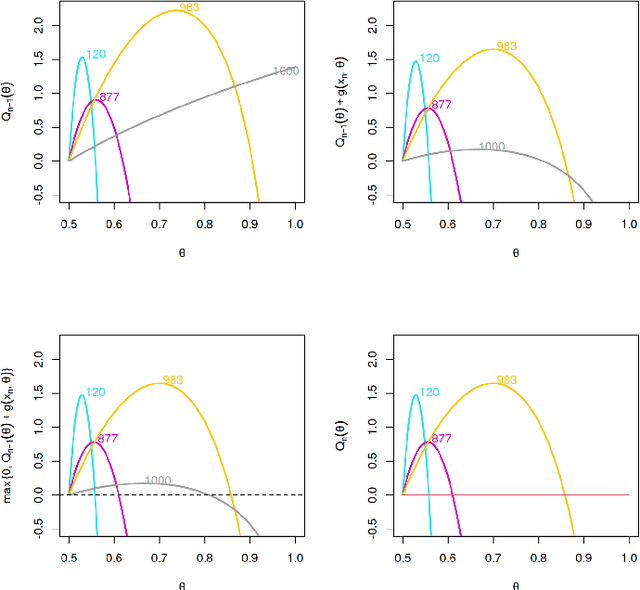
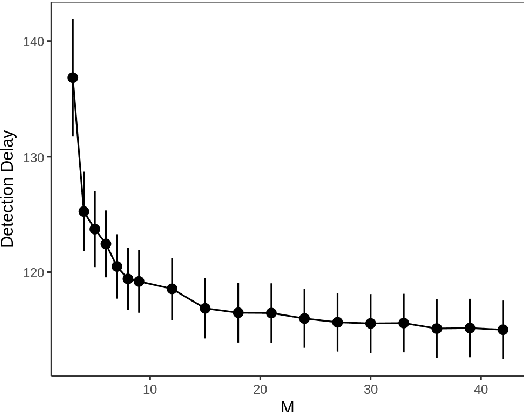
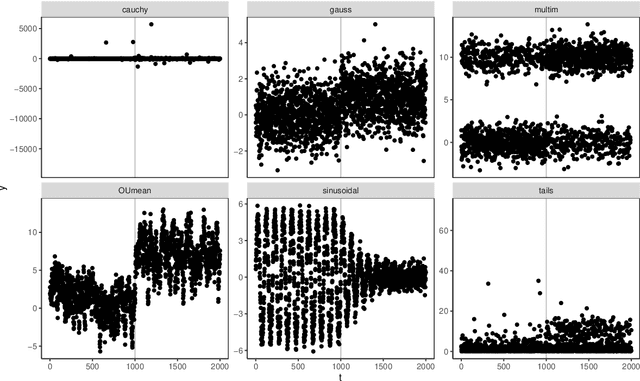
Online changepoint detection aims to detect anomalies and changes in real-time in high-frequency data streams, sometimes with limited available computational resources. This is an important task that is rooted in many real-world applications, including and not limited to cybersecurity, medicine and astrophysics. While fast and efficient online algorithms have been recently introduced, these rely on parametric assumptions which are often violated in practical applications. Motivated by data streams from the telecommunications sector, we build a flexible nonparametric approach to detect a change in the distribution of a sequence. Our procedure, NP-FOCuS, builds a sequential likelihood ratio test for a change in a set of points of the empirical cumulative density function of our data. This is achieved by keeping track of the number of observations above or below those points. Thanks to functional pruning ideas, NP-FOCuS has a computational cost that is log-linear in the number of observations and is suitable for high-frequency data streams. In terms of detection power, NP-FOCuS is seen to outperform current nonparametric online changepoint techniques in a variety of settings. We demonstrate the utility of the procedure on both simulated and real data.

Automatic Change-Point Detection in Time Series via Deep Learning

Detecting change-points in data is challenging because of the range of possible types of change and types of behaviour of data when there is no change. Statistically efficient methods for detecting a change will depend on both of these features, and it can be difficult for a practitioner to develop an appropriate detection method for their application of interest. We show how to automatically generate new detection methods based on training a neural network. Our approach is motivated by many existing tests for the presence of a change-point being able to be represented by a simple neural network, and thus a neural network trained with sufficient data should have performance at least as good as these methods. We present theory that quantifies the error rate for such an approach, and how it depends on the amount of training data. Empirical results show that, even with limited training data, its performance is competitive with the standard CUSUM test for detecting a change in mean when the noise is independent and Gaussian, and can substantially outperform it in the presence of auto-correlated or heavy-tailed noise. Our method also shows strong results in detecting and localising changes in activity based on accelerometer data.

Preferential Subsampling for Stochastic Gradient Langevin Dynamics

Stochastic gradient MCMC (SGMCMC) offers a scalable alternative to traditional MCMC, by constructing an unbiased estimate of the gradient of the log-posterior with a small, uniformly-weighted subsample of the data. While efficient to compute, the resulting gradient estimator may exhibit a high variance and impact sampler performance. The problem of variance control has been traditionally addressed by constructing a better stochastic gradient estimator, often using control variates. We propose to use a discrete, non-uniform probability distribution to preferentially subsample data points that have a greater impact on the stochastic gradient. In addition, we present a method of adaptively adjusting the subsample size at each iteration of the algorithm, so that we increase the subsample size in areas of the sample space where the gradient is harder to estimate. We demonstrate that such an approach can maintain the same level of accuracy while substantially reducing the average subsample size that is used.

Continuously-Tempered PDMP Samplers

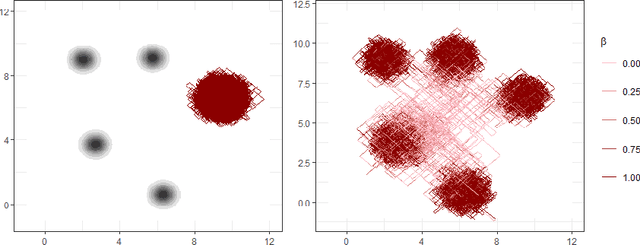
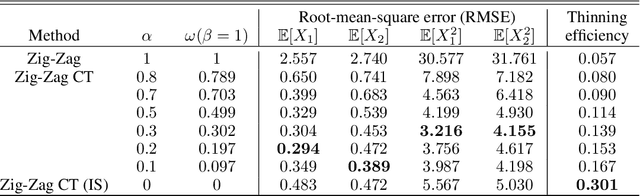
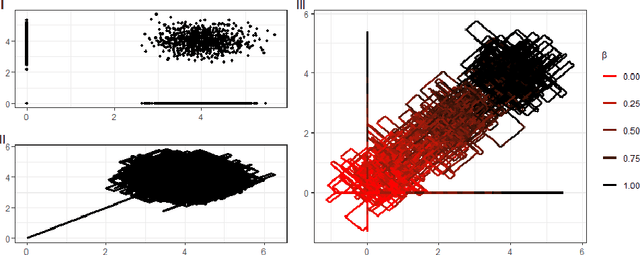
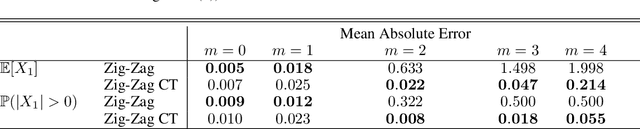
New sampling algorithms based on simulating continuous-time stochastic processes called piece-wise deterministic Markov processes (PDMPs) have shown considerable promise. However, these methods can struggle to sample from multi-modal or heavy-tailed distributions. We show how tempering ideas can improve the mixing of PDMPs in such cases. We introduce an extended distribution defined over the state of the posterior distribution and an inverse temperature, which interpolates between a tractable distribution when the inverse temperature is 0 and the posterior when the inverse temperature is 1. The marginal distribution of the inverse temperature is a mixture of a continuous distribution on [0,1) and a point mass at 1: which means that we obtain samples when the inverse temperature is 1, and these are draws from the posterior, but sampling algorithms will also explore distributions at lower temperatures which will improve mixing. We show how PDMPs, and particularly the Zig-Zag sampler, can be implemented to sample from such an extended distribution. The resulting algorithm is easy to implement and we show empirically that it can outperform existing PDMP-based samplers on challenging multimodal posteriors.

Efficient computation of the volume of a polytope in high-dimensions using Piecewise Deterministic Markov Processes

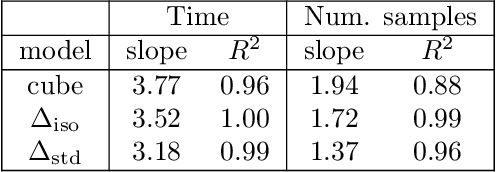
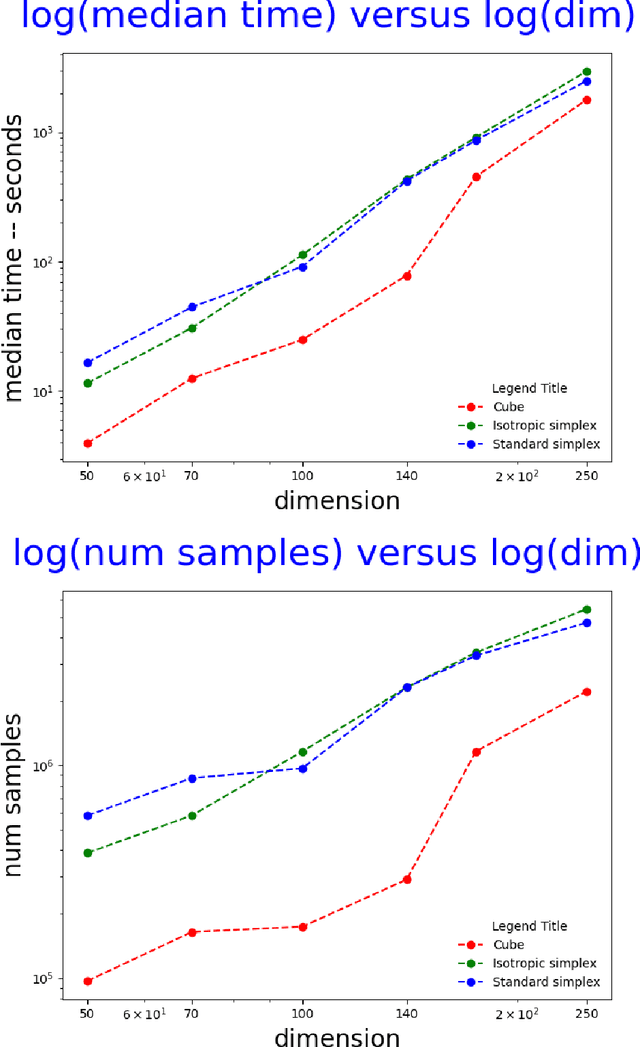
Computing the volume of a polytope in high dimensions is computationally challenging but has wide applications. Current state-of-the-art algorithms to compute such volumes rely on efficient sampling of a Gaussian distribution restricted to the polytope, using e.g. Hamiltonian Monte Carlo. We present a new sampling strategy that uses a Piecewise Deterministic Markov Process. Like Hamiltonian Monte Carlo, this new method involves simulating trajectories of a non-reversible process and inherits similar good mixing properties. However, importantly, the process can be simulated more easily due to its piecewise linear trajectories - and this leads to a reduction of the computational cost by a factor of the dimension of the space. Our experiments indicate that our method is numerically robust and is one order of magnitude faster (or better) than existing methods using Hamiltonian Monte Carlo. On a single core processor, we report computational time of a few minutes up to dimension 500.

Fast Online Changepoint Detection via Functional Pruning CUSUM statistics

Many modern applications of online changepoint detection require the ability to process high-frequency observations, sometimes with limited available computational resources. Online algorithms for detecting a change in mean often involve using a moving window, or specifying the expected size of change. Such choices affect which changes the algorithms have most power to detect. We introduce an algorithm, Functional Online CuSUM (FOCuS), which is equivalent to running these earlier methods simultaneously for all sizes of window, or all possible values for the size of change. Our theoretical results give tight bounds on the expected computational cost per iteration of FOCuS, with this being logarithmic in the number of observations. We show how FOCuS can be applied to a number of different change in mean scenarios, and demonstrate its practical utility through its state-of-the art performance at detecting anomalous behaviour in computer server data.

Reversible Jump PDMP Samplers for Variable Selection

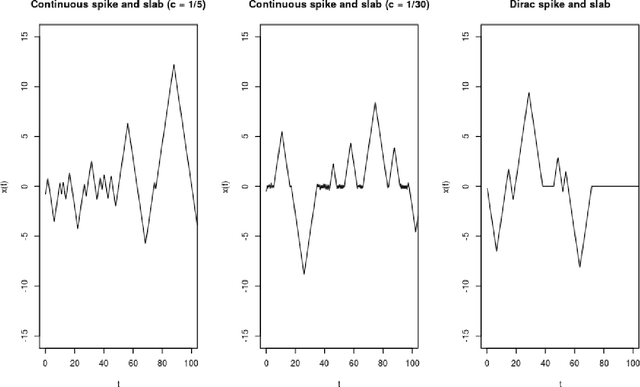
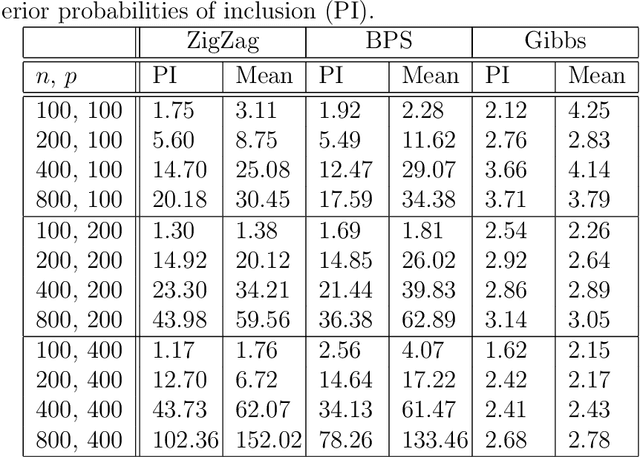
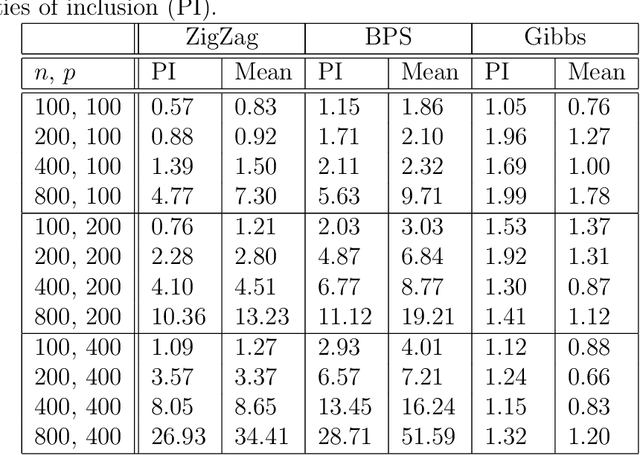
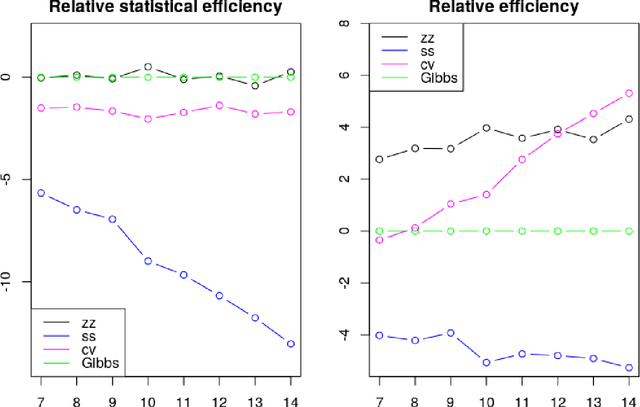
A new class of Markov chain Monte Carlo (MCMC) algorithms, based on simulating piecewise deterministic Markov processes (PDMPs), have recently shown great promise: they are non-reversible, can mix better than standard MCMC algorithms, and can use subsampling ideas to speed up computation in big data scenarios. However, current PDMP samplers can only sample from posterior densities that are differentiable almost everywhere, which precludes their use for model choice. Motivated by variable selection problems, we show how to develop reversible jump PDMP samplers that can jointly explore the discrete space of models and the continuous space of parameters. Our framework is general: it takes any existing PDMP sampler, and adds two types of trans-dimensional moves that allow for the addition or removal of a variable from the model. We show how the rates of these trans-dimensional moves can be calculated so that the sampler has the correct invariant distribution. Simulations show that the new samplers can mix better than standard MCMC algorithms. Our empirical results show they are also more efficient than gradient-based samplers that avoid model choice through use of continuous spike-and-slab priors which replace a point mass at zero for each parameter with a density concentrated around zero.