A PAC-Bayesian Perspective on the Interpolating Information Criterion

Deep learning is renowned for its theory-practice gap, whereby principled theory typically fails to provide much beneficial guidance for implementation in practice. This has been highlighted recently by the benign overfitting phenomenon: when neural networks become sufficiently large to interpolate the dataset perfectly, model performance appears to improve with increasing model size, in apparent contradiction with the well-known bias-variance tradeoff. While such phenomena have proven challenging to theoretically study for general models, the recently proposed Interpolating Information Criterion (IIC) provides a valuable theoretical framework to examine performance for overparameterized models. Using the IIC, a PAC-Bayes bound is obtained for a general class of models, characterizing factors which influence generalization performance in the interpolating regime. From the provided bound, we quantify how the test error for overparameterized models achieving effectively zero training error depends on the quality of the implicit regularization imposed by e.g. the combination of model, optimizer, and parameter-initialization scheme; the spectrum of the empirical neural tangent kernel; curvature of the loss landscape; and noise present in the data.

Deep Generative Models, Synthetic Tabular Data, and Differential Privacy: An Overview and Synthesis

This article provides a comprehensive synthesis of the recent developments in synthetic data generation via deep generative models, focusing on tabular datasets. We specifically outline the importance of synthetic data generation in the context of privacy-sensitive data. Additionally, we highlight the advantages of using deep generative models over other methods and provide a detailed explanation of the underlying concepts, including unsupervised learning, neural networks, and generative models. The paper covers the challenges and considerations involved in using deep generative models for tabular datasets, such as data normalization, privacy concerns, and model evaluation. This review provides a valuable resource for researchers and practitioners interested in synthetic data generation and its applications.

The Interpolating Information Criterion for Overparameterized Models

The problem of model selection is considered for the setting of interpolating estimators, where the number of model parameters exceeds the size of the dataset. Classical information criteria typically consider the large-data limit, penalizing model size. However, these criteria are not appropriate in modern settings where overparameterized models tend to perform well. For any overparameterized model, we show that there exists a dual underparameterized model that possesses the same marginal likelihood, thus establishing a form of Bayesian duality. This enables more classical methods to be used in the overparameterized setting, revealing the Interpolating Information Criterion, a measure of model quality that naturally incorporates the choice of prior into the model selection. Our new information criterion accounts for prior misspecification, geometric and spectral properties of the model, and is numerically consistent with known empirical and theoretical behavior in this regime.

Graph Neural Network-Based Anomaly Detection for River Network Systems

Water is the lifeblood of river networks, and its quality plays a crucial role in sustaining both aquatic ecosystems and human societies. Real-time monitoring of water quality is increasingly reliant on in-situ sensor technology. Anomaly detection is crucial for identifying erroneous patterns in sensor data, but can be a challenging task due to the complexity and variability of the data, even under normal conditions. This paper presents a solution to the challenging task of anomaly detection for river network sensor data, which is essential for accurate and continuous monitoring. We use a graph neural network model, the recently proposed Graph Deviation Network (GDN), which employs graph attention-based forecasting to capture the complex spatio-temporal relationships between sensors. We propose an alternate anomaly scoring method, GDN+, based on the learned graph. To evaluate the model's efficacy, we introduce new benchmarking simulation experiments with highly-sophisticated dependency structures and subsequence anomalies of various types. We further examine the strengths and weaknesses of this baseline approach, GDN, in comparison to other benchmarking methods on complex real-world river network data. Findings suggest that GDN+ outperforms the baseline approach in high-dimensional data, while also providing improved interpretability. We also introduce software called gnnad.

Federated Variational Inference Methods for Structured Latent Variable Models

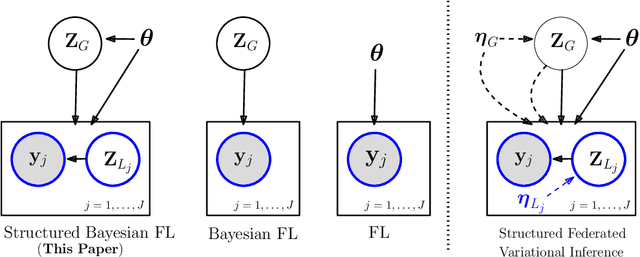
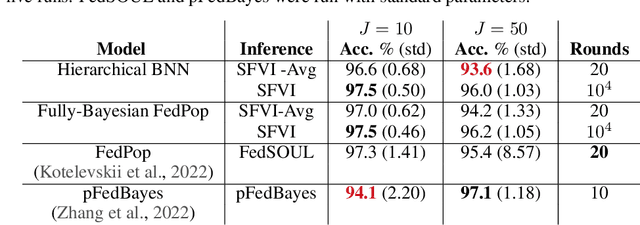
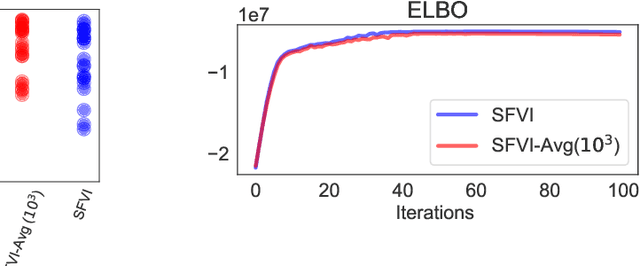
Federated learning methods, that is, methods that perform model training using data situated across different sources, whilst simultaneously not having the data leave their original source, are of increasing interest in a number of fields. However, despite this interest, the classes of models for which easily-applicable and sufficiently general approaches are available is limited, excluding many structured probabilistic models. We present a general yet elegant resolution to the aforementioned issue. The approach is based on adopting structured variational inference, an approach widely used in Bayesian machine learning, to the federated setting. Additionally, a communication-efficient variant analogous to the canonical FedAvg algorithm is explored. The effectiveness of the proposed algorithms are demonstrated, and their performance is compared on Bayesian multinomial regression, topic modelling, and mixed model examples.

Transport Reversible Jump Proposals

Reversible jump Markov chain Monte Carlo (RJMCMC) proposals that achieve reasonable acceptance rates and mixing are notoriously difficult to design in most applications. Inspired by recent advances in deep neural network-based normalizing flows and density estimation, we demonstrate an approach to enhance the efficiency of RJMCMC sampling by performing transdimensional jumps involving reference distributions. In contrast to other RJMCMC proposals, the proposed method is the first to apply a non-linear transport-based approach to construct efficient proposals between models with complicated dependency structures. It is shown that, in the setting where exact transports are used, our RJMCMC proposals have the desirable property that the acceptance probability depends only on the model probabilities. Numerical experiments demonstrate the efficacy of the approach.

Continuously-Tempered PDMP Samplers

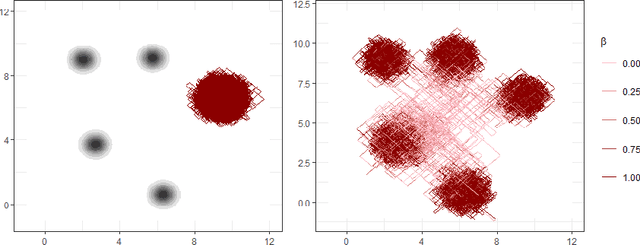
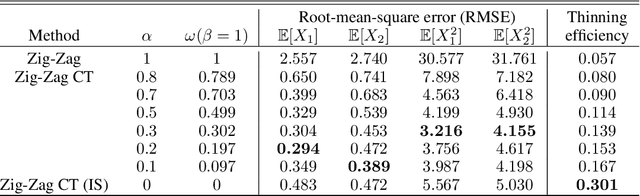
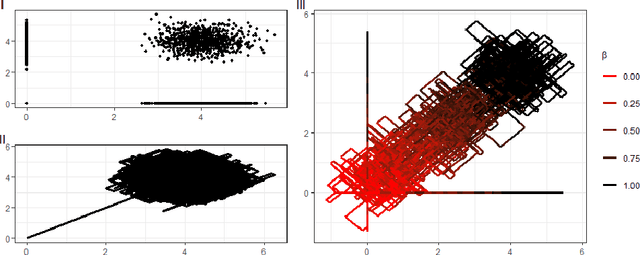
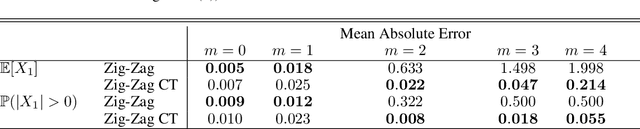
New sampling algorithms based on simulating continuous-time stochastic processes called piece-wise deterministic Markov processes (PDMPs) have shown considerable promise. However, these methods can struggle to sample from multi-modal or heavy-tailed distributions. We show how tempering ideas can improve the mixing of PDMPs in such cases. We introduce an extended distribution defined over the state of the posterior distribution and an inverse temperature, which interpolates between a tractable distribution when the inverse temperature is 0 and the posterior when the inverse temperature is 1. The marginal distribution of the inverse temperature is a mixture of a continuous distribution on [0,1) and a point mass at 1: which means that we obtain samples when the inverse temperature is 1, and these are draws from the posterior, but sampling algorithms will also explore distributions at lower temperatures which will improve mixing. We show how PDMPs, and particularly the Zig-Zag sampler, can be implemented to sample from such an extended distribution. The resulting algorithm is easy to implement and we show empirically that it can outperform existing PDMP-based samplers on challenging multimodal posteriors.

The reproducing Stein kernel approach for post-hoc corrected sampling

Stein importance sampling is a widely applicable technique based on kernelized Stein discrepancy, which corrects the output of approximate sampling algorithms by reweighting the empirical distribution of the samples. A general analysis of this technique is conducted for the previously unconsidered setting where samples are obtained via the simulation of a Markov chain, and applies to an arbitrary underlying Polish space. We prove that Stein importance sampling yields consistent estimators for quantities related to a target distribution of interest by using samples obtained from a geometrically ergodic Markov chain with a possibly unknown invariant measure that differs from the desired target. The approach is shown to be valid under conditions that are satisfied for a large number of unadjusted samplers, and is capable of retaining consistency when data subsampling is used. Along the way, a universal theory of reproducing Stein kernels is established, which enables the construction of kernelized Stein discrepancy on general Polish spaces, and provides sufficient conditions for kernels to be convergence-determining on such spaces. These results are of independent interest for the development of future methodology based on kernelized Stein discrepancies.

Implicit Langevin Algorithms for Sampling From Log-concave Densities

For sampling from a log-concave density, we study implicit integrators resulting from $\theta$-method discretization of the overdamped Langevin diffusion stochastic differential equation. Theoretical and algorithmic properties of the resulting sampling methods for $ \theta \in [0,1] $ and a range of step sizes are established. Our results generalize and extend prior works in several directions. In particular, for $\theta\ge1/2$, we prove geometric ergodicity and stability of the resulting methods for all step sizes. We show that obtaining subsequent samples amounts to solving a strongly-convex optimization problem, which is readily achievable using one of numerous existing methods. Numerical examples supporting our theoretical analysis are also presented.