Understanding the Implicit Biases of Design Choices for Time Series Foundation Models

Time series foundation models (TSFMs) are a class of potentially powerful, general-purpose tools for time series forecasting and related temporal tasks, but their behavior is strongly shaped by subtle inductive biases in their design. Rather than developing a new model and claiming that it is better than existing TSFMs, e.g., by winning on existing well-established benchmarks, our objective is to understand how the various ``knobs'' of the training process affect model quality. Using a mix of theory and controlled empirical evaluation, we identify several design choices (patch size, embedding choice, training objective, etc.) and show how they lead to implicit biases in fundamental model properties (temporal behavior, geometric structure, how aggressively or not the model regresses to the mean, etc.); and we show how these biases can be intuitive or very counterintuitive, depending on properties of the model and data. We also illustrate in a case study on outlier handling how multiple biases can interact in complex ways; and we discuss implications of our results for learning the bitter lesson and building TSFMs.

Forking-Sequences

While accuracy is a critical requirement for time series forecasting models, an equally important (yet often overlooked) desideratum is forecast stability across forecast creation dates (FCDs). Even highly accurate models can produce erratic revisions between FCDs, undermining stakeholder trust and disrupting downstream decision-making. To improve forecast stability, models like MQCNN, MQT, and SPADE employ a little-known but highly effective technique: forking-sequences. Unlike standard statistical and neural forecasting methods that treat each FCD independently, the forking-sequences method jointly encodes and decodes the entire time series across all FCDs, in a way mirroring time series cross-validation. Since forking sequences remains largely unknown in the broader neural forecasting community, in this work, we formalize the forking-sequences approach, and we make a case for its broader adoption. We demonstrate three key benefits of forking-sequences: (i) more stable and consistent gradient updates during training; (ii) reduced forecast variance through ensembling; and (iii) improved inference computational efficiency. We validate forking-sequences' benefits using 16 datasets from the M1, M3, M4, and Tourism competitions, showing improvements in forecast percentage change stability of 28.8%, 28.8%, 37.9%, and 31.3%, and 8.8%, on average, for MLP, RNN, LSTM, CNN, and Transformer-based architectures, respectively.

Efficiently Generating Correlated Sample Paths from Multi-step Time Series Foundation Models

Many time series applications require access to multi-step forecast trajectories in the form of sample paths. Recently, time series foundation models have leveraged multi-step lookahead predictions to improve the quality and efficiency of multi-step forecasts. However, these models only predict independent marginal distributions for each time step, rather than a full joint predictive distribution. To generate forecast sample paths with realistic correlation structures, one typically resorts to autoregressive sampling, which can be extremely expensive. In this paper, we present a copula-based approach to efficiently generate accurate, correlated sample paths from existing multi-step time series foundation models in one forward pass. Our copula-based approach generates correlated sample paths orders of magnitude faster than autoregressive sampling, and it yields improved sample path quality by mitigating the snowballing error phenomenon.

XQuant: Breaking the Memory Wall for LLM Inference with KV Cache Rematerialization

Although LLM inference has emerged as a critical workload for many downstream applications, efficiently inferring LLMs is challenging due to the substantial memory footprint and bandwidth requirements. In parallel, compute capabilities have steadily outpaced both memory capacity and bandwidth over the last few decades, a trend that remains evident in modern GPU hardware and exacerbates the challenge of LLM inference. As such, new algorithms are emerging that trade increased computation for reduced memory operations. To that end, we present XQuant, which takes advantage of this trend, enabling an order-of-magnitude reduction in memory consumption through low-bit quantization with substantial accuracy benefits relative to state-of-the-art KV cache quantization methods. We accomplish this by quantizing and caching the layer input activations X, instead of using standard KV caching, and then rematerializing the Keys and Values on-the-fly during inference. This results in an immediate 2$\times$ memory savings compared to KV caching. By applying XQuant, we achieve up to $\sim 7.7\times$ memory savings with $<0.1$ perplexity degradation compared to the FP16 baseline. Furthermore, our approach leverages the fact that X values are similar across layers. Building on this observation, we introduce XQuant-CL, which exploits the cross-layer similarity in the X embeddings for extreme compression. Across different models, XQuant-CL attains up to 10$\times$ memory savings relative to the FP16 baseline with only 0.01 perplexity degradation, and 12.5$\times$ memory savings with only $0.1$ perplexity degradation. XQuant exploits the rapidly increasing compute capabilities of hardware platforms to eliminate the memory bottleneck, while surpassing state-of-the-art KV cache quantization methods and achieving near-FP16 accuracy across a wide range of models.

Random Matrix Theory for Deep Learning: Beyond Eigenvalues of Linear Models

Modern Machine Learning (ML) and Deep Neural Networks (DNNs) often operate on high-dimensional data and rely on overparameterized models, where classical low-dimensional intuitions break down. In particular, the proportional regime where the data dimension, sample size, and number of model parameters are all large and comparable, gives rise to novel and sometimes counterintuitive behaviors. This paper extends traditional Random Matrix Theory (RMT) beyond eigenvalue-based analysis of linear models to address the challenges posed by nonlinear ML models such as DNNs in this regime. We introduce the concept of High-dimensional Equivalent, which unifies and generalizes both Deterministic Equivalent and Linear Equivalent, to systematically address three technical challenges: high dimensionality, nonlinearity, and the need to analyze generic eigenspectral functionals. Leveraging this framework, we provide precise characterizations of the training and generalization performance of linear models, nonlinear shallow networks, and deep networks. Our results capture rich phenomena, including scaling laws, double descent, and nonlinear learning dynamics, offering a unified perspective on the theoretical understanding of deep learning in high dimensions.

Multipole Attention for Efficient Long Context Reasoning

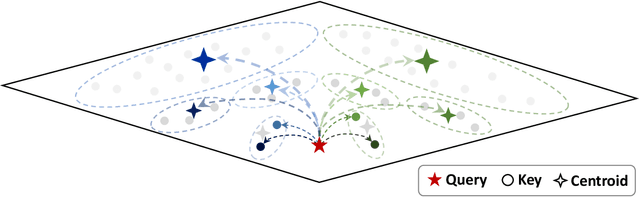
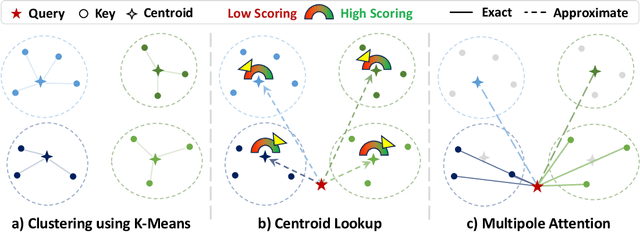
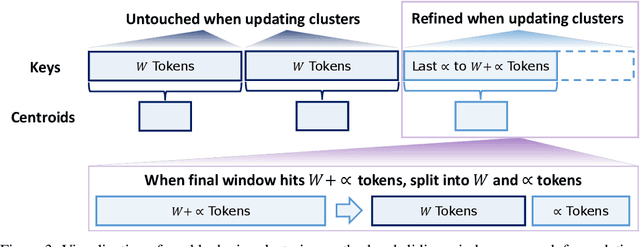
Large Reasoning Models (LRMs) have shown promising accuracy improvements on complex problem-solving tasks. While these models have attained high accuracy by leveraging additional computation at test time, they need to generate long chain-of-thought reasoning in order to think before answering, which requires generating thousands of tokens. While sparse attention methods can help reduce the KV cache pressure induced by this long autoregressive reasoning, these methods can introduce errors which disrupt the reasoning process. Additionally, prior methods often pre-process the input to make it easier to identify the important prompt tokens when computing attention during generation, and this pre-processing is challenging to perform online for newly generated reasoning tokens. Our work addresses these challenges by introducing Multipole Attention, which accelerates autoregressive reasoning by only computing exact attention for the most important tokens, while maintaining approximate representations for the remaining tokens. Our method first performs clustering to group together semantically similar key vectors, and then uses the cluster centroids both to identify important key vectors and to approximate the remaining key vectors in order to retain high accuracy. We design a fast cluster update process to quickly re-cluster the input and previously generated tokens, thereby allowing for accelerating attention to the previous output tokens. We evaluate our method using emerging LRMs such as Qwen-8B, demonstrating that our approach can maintain accuracy on complex reasoning tasks even with aggressive attention sparsity settings. We also provide kernel implementations to demonstrate the practical efficiency gains from our method, achieving up to 4.5$\times$ speedup for attention in long-context reasoning applications. Our code is available at https://github.com/SqueezeAILab/MultipoleAttention.

Spectral Estimation with Free Decompression

Computing eigenvalues of very large matrices is a critical task in many machine learning applications, including the evaluation of log-determinants, the trace of matrix functions, and other important metrics. As datasets continue to grow in scale, the corresponding covariance and kernel matrices become increasingly large, often reaching magnitudes that make their direct formation impractical or impossible. Existing techniques typically rely on matrix-vector products, which can provide efficient approximations, if the matrix spectrum behaves well. However, in settings like distributed learning, or when the matrix is defined only indirectly, access to the full data set can be restricted to only very small sub-matrices of the original matrix. In these cases, the matrix of nominal interest is not even available as an implicit operator, meaning that even matrix-vector products may not be available. In such settings, the matrix is "impalpable," in the sense that we have access to only masked snapshots of it. We draw on principles from free probability theory to introduce a novel method of "free decompression" to estimate the spectrum of such matrices. Our method can be used to extrapolate from the empirical spectral densities of small submatrices to infer the eigenspectrum of extremely large (impalpable) matrices (that we cannot form or even evaluate with full matrix-vector products). We demonstrate the effectiveness of this approach through a series of examples, comparing its performance against known limiting distributions from random matrix theory in synthetic settings, as well as applying it to submatrices of real-world datasets, matching them with their full empirical eigenspectra.

End-to-End Probabilistic Framework for Learning with Hard Constraints

We present a general purpose probabilistic forecasting framework, ProbHardE2E, to learn systems that can incorporate operational/physical constraints as hard requirements. ProbHardE2E enforces hard constraints by exploiting variance information in a novel way; and thus it is also capable of performing uncertainty quantification (UQ) on the model. Our methodology uses a novel differentiable probabilistic projection layer (DPPL) that can be combined with a wide range of neural network architectures. This DPPL allows the model to learn the system in an end-to-end manner, compared to other approaches where the constraints are satisfied either through a post-processing step or at inference. In addition, ProbHardE2E can optimize a strictly proper scoring rule, without making any distributional assumptions on the target, which enables it to obtain robust distributional estimates (in contrast to existing approaches that generally optimize likelihood-based objectives, which are heavily biased by their distributional assumptions and model choices); and it can incorporate a range of non-linear constraints (increasing the power of modeling and flexibility). We apply ProbHardE2E to problems in learning partial differential equations with uncertainty estimates and to probabilistic time-series forecasting, showcasing it as a broadly applicable general setup that connects these seemingly disparate domains.

FLEX: A Backbone for Diffusion-Based Modeling of Spatio-temporal Physical Systems

We introduce FLEX (FLow EXpert), a backbone architecture for generative modeling of spatio-temporal physical systems using diffusion models. FLEX operates in the residual space rather than on raw data, a modeling choice that we motivate theoretically, showing that it reduces the variance of the velocity field in the diffusion model, which helps stabilize training. FLEX integrates a latent Transformer into a U-Net with standard convolutional ResNet layers and incorporates a redesigned skip connection scheme. This hybrid design enables the model to capture both local spatial detail and long-range dependencies in latent space. To improve spatio-temporal conditioning, FLEX uses a task-specific encoder that processes auxiliary inputs such as coarse or past snapshots. Weak conditioning is applied to the shared encoder via skip connections to promote generalization, while strong conditioning is applied to the decoder through both skip and bottleneck features to ensure reconstruction fidelity. FLEX achieves accurate predictions for super-resolution and forecasting tasks using as few as two reverse diffusion steps. It also produces calibrated uncertainty estimates through sampling. Evaluations on high-resolution 2D turbulence data show that FLEX outperforms strong baselines and generalizes to out-of-distribution settings, including unseen Reynolds numbers, physical observables (e.g., fluid flow velocity fields), and boundary conditions.

Removing Watermarks with Partial Regeneration using Semantic Information

As AI-generated imagery becomes ubiquitous, invisible watermarks have emerged as a primary line of defense for copyright and provenance. The newest watermarking schemes embed semantic signals - content-aware patterns that are designed to survive common image manipulations - yet their true robustness against adaptive adversaries remains under-explored. We expose a previously unreported vulnerability and introduce SemanticRegen, a three-stage, label-free attack that erases state-of-the-art semantic and invisible watermarks while leaving an image's apparent meaning intact. Our pipeline (i) uses a vision-language model to obtain fine-grained captions, (ii) extracts foreground masks with zero-shot segmentation, and (iii) inpaints only the background via an LLM-guided diffusion model, thereby preserving salient objects and style cues. Evaluated on 1,000 prompts across four watermarking systems - TreeRing, StegaStamp, StableSig, and DWT/DCT - SemanticRegen is the only method to defeat the semantic TreeRing watermark (p = 0.10 > 0.05) and reduces bit-accuracy below 0.75 for the remaining schemes, all while maintaining high perceptual quality (masked SSIM = 0.94 +/- 0.01). We further introduce masked SSIM (mSSIM) to quantify fidelity within foreground regions, showing that our attack achieves up to 12 percent higher mSSIM than prior diffusion-based attackers. These results highlight an urgent gap between current watermark defenses and the capabilities of adaptive, semantics-aware adversaries, underscoring the need for watermarking algorithms that are resilient to content-preserving regenerative attacks.