Hanyu Zhang
The Forecast Critic: Leveraging Large Language Models for Poor Forecast Identification
Dec 12, 2025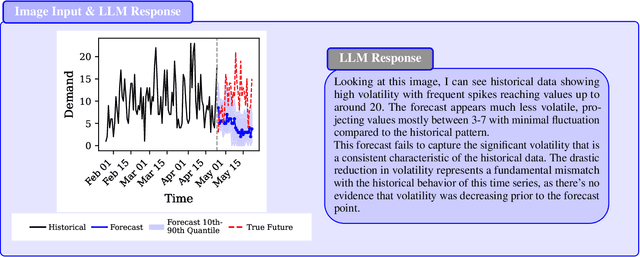
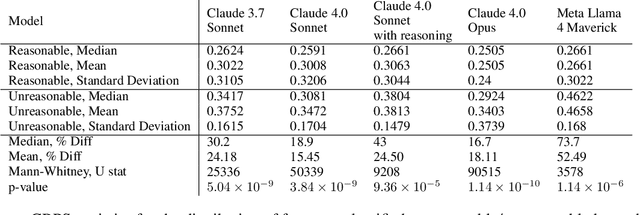


Abstract:Monitoring forecasting systems is critical for customer satisfaction, profitability, and operational efficiency in large-scale retail businesses. We propose The Forecast Critic, a system that leverages Large Language Models (LLMs) for automated forecast monitoring, taking advantage of their broad world knowledge and strong ``reasoning'' capabilities. As a prerequisite for this, we systematically evaluate the ability of LLMs to assess time series forecast quality, focusing on three key questions. (1) Can LLMs be deployed to perform forecast monitoring and identify obviously unreasonable forecasts? (2) Can LLMs effectively incorporate unstructured exogenous features to assess what a reasonable forecast looks like? (3) How does performance vary across model sizes and reasoning capabilities, measured across state-of-the-art LLMs? We present three experiments, including on both synthetic and real-world forecasting data. Our results show that LLMs can reliably detect and critique poor forecasts, such as those plagued by temporal misalignment, trend inconsistencies, and spike errors. The best-performing model we evaluated achieves an F1 score of 0.88, somewhat below human-level performance (F1 score: 0.97). We also demonstrate that multi-modal LLMs can effectively incorporate unstructured contextual signals to refine their assessment of the forecast. Models correctly identify missing or spurious promotional spikes when provided with historical context about past promotions (F1 score: 0.84). Lastly, we demonstrate that these techniques succeed in identifying inaccurate forecasts on the real-world M5 time series dataset, with unreasonable forecasts having an sCRPS at least 10% higher than that of reasonable forecasts. These findings suggest that LLMs, even without domain-specific fine-tuning, may provide a viable and scalable option for automated forecast monitoring and evaluation.
Mind the Gaps: Auditing and Reducing Group Inequity in Large-Scale Mobility Prediction
Oct 30, 2025Abstract:Next location prediction underpins a growing number of mobility, retail, and public-health applications, yet its societal impacts remain largely unexplored. In this paper, we audit state-of-the-art mobility prediction models trained on a large-scale dataset, highlighting hidden disparities based on user demographics. Drawing from aggregate census data, we compute the difference in predictive performance on racial and ethnic user groups and show a systematic disparity resulting from the underlying dataset, resulting in large differences in accuracy based on location and user groups. To address this, we propose Fairness-Guided Incremental Sampling (FGIS), a group-aware sampling strategy designed for incremental data collection settings. Because individual-level demographic labels are unavailable, we introduce Size-Aware K-Means (SAKM), a clustering method that partitions users in latent mobility space while enforcing census-derived group proportions. This yields proxy racial labels for the four largest groups in the state: Asian, Black, Hispanic, and White. Built on these labels, our sampling algorithm prioritizes users based on expected performance gains and current group representation. This method incrementally constructs training datasets that reduce demographic performance gaps while preserving overall accuracy. Our method reduces total disparity between groups by up to 40\% with minimal accuracy trade-offs, as evaluated on a state-of-art MetaPath2Vec model and a transformer-encoder model. Improvements are most significant in early sampling stages, highlighting the potential for fairness-aware strategies to deliver meaningful gains even in low-resource settings. Our findings expose structural inequities in mobility prediction pipelines and demonstrate how lightweight, data-centric interventions can improve fairness with little added complexity, especially for low-data applications.
Efficiently Generating Correlated Sample Paths from Multi-step Time Series Foundation Models
Oct 02, 2025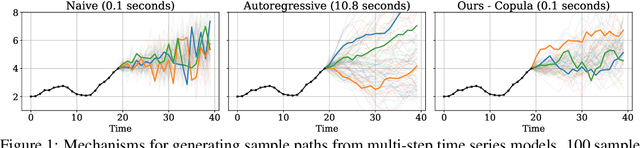
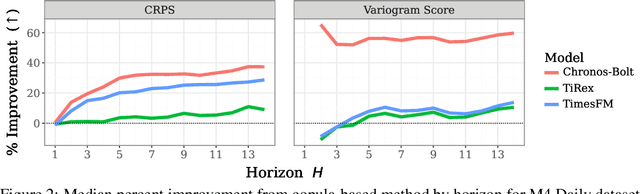
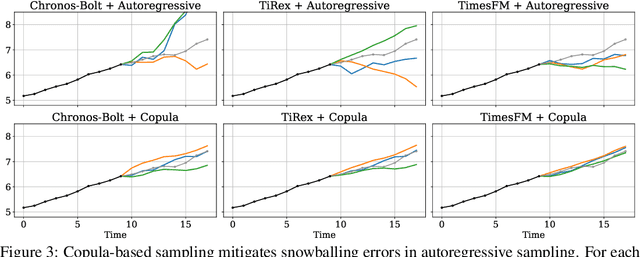
Abstract:Many time series applications require access to multi-step forecast trajectories in the form of sample paths. Recently, time series foundation models have leveraged multi-step lookahead predictions to improve the quality and efficiency of multi-step forecasts. However, these models only predict independent marginal distributions for each time step, rather than a full joint predictive distribution. To generate forecast sample paths with realistic correlation structures, one typically resorts to autoregressive sampling, which can be extremely expensive. In this paper, we present a copula-based approach to efficiently generate accurate, correlated sample paths from existing multi-step time series foundation models in one forward pass. Our copula-based approach generates correlated sample paths orders of magnitude faster than autoregressive sampling, and it yields improved sample path quality by mitigating the snowballing error phenomenon.
GLM-4.5: Agentic, Reasoning, and Coding (ARC) Foundation Models
Aug 08, 2025Abstract:We present GLM-4.5, an open-source Mixture-of-Experts (MoE) large language model with 355B total parameters and 32B activated parameters, featuring a hybrid reasoning method that supports both thinking and direct response modes. Through multi-stage training on 23T tokens and comprehensive post-training with expert model iteration and reinforcement learning, GLM-4.5 achieves strong performance across agentic, reasoning, and coding (ARC) tasks, scoring 70.1% on TAU-Bench, 91.0% on AIME 24, and 64.2% on SWE-bench Verified. With much fewer parameters than several competitors, GLM-4.5 ranks 3rd overall among all evaluated models and 2nd on agentic benchmarks. We release both GLM-4.5 (355B parameters) and a compact version, GLM-4.5-Air (106B parameters), to advance research in reasoning and agentic AI systems. Code, models, and more information are available at https://github.com/zai-org/GLM-4.5.
Gradient-Adaptive Policy Optimization: Towards Multi-Objective Alignment of Large Language Models
Jul 02, 2025Abstract:Reinforcement Learning from Human Feedback (RLHF) has emerged as a powerful technique for aligning large language models (LLMs) with human preferences. However, effectively aligning LLMs with diverse human preferences remains a significant challenge, particularly when they are conflict. To address this issue, we frame human value alignment as a multi-objective optimization problem, aiming to maximize a set of potentially conflicting objectives. We introduce Gradient-Adaptive Policy Optimization (GAPO), a novel fine-tuning paradigm that employs multiple-gradient descent to align LLMs with diverse preference distributions. GAPO adaptively rescales the gradients for each objective to determine an update direction that optimally balances the trade-offs between objectives. Additionally, we introduce P-GAPO, which incorporates user preferences across different objectives and achieves Pareto solutions that better align with the user's specific needs. Our theoretical analysis demonstrates that GAPO converges towards a Pareto optimal solution for multiple objectives. Empirical results on Mistral-7B show that GAPO outperforms current state-of-the-art methods, achieving superior performance in both helpfulness and harmlessness.
Non-Uniform Class-Wise Coreset Selection: Characterizing Category Difficulty for Data-Efficient Transfer Learning
Apr 17, 2025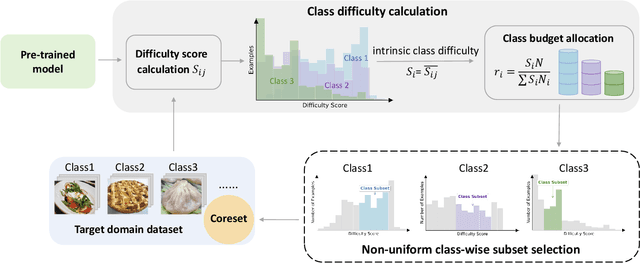

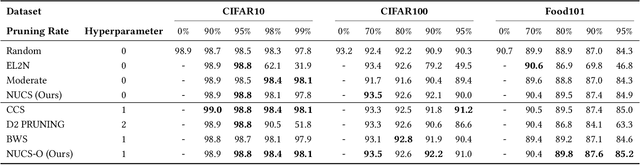
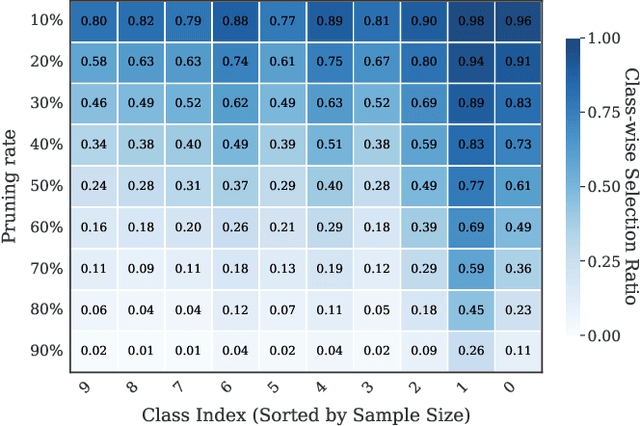
Abstract:As transfer learning models and datasets grow larger, efficient adaptation and storage optimization have become critical needs. Coreset selection addresses these challenges by identifying and retaining the most informative samples, constructing a compact subset for target domain training. However, current methods primarily rely on instance-level difficulty assessments, overlooking crucial category-level characteristics and consequently under-representing minority classes. To overcome this limitation, we propose Non-Uniform Class-Wise Coreset Selection (NUCS), a novel framework that integrates both class-level and instance-level criteria. NUCS automatically allocates data selection budgets for each class based on intrinsic category difficulty and adaptively selects samples within optimal difficulty ranges. By explicitly incorporating category-specific insights, our approach achieves a more balanced and representative coreset, addressing key shortcomings of prior methods. Comprehensive theoretical analysis validates the rationale behind adaptive budget allocation and sample selection, while extensive experiments across 14 diverse datasets and model architectures demonstrate NUCS's consistent improvements over state-of-the-art methods, achieving superior accuracy and computational efficiency. Notably, on CIFAR100 and Food101, NUCS matches full-data training accuracy while retaining just 30% of samples and reducing computation time by 60%. Our work highlights the importance of characterizing category difficulty in coreset selection, offering a robust and data-efficient solution for transfer learning.
Controlling Large Language Models Through Concept Activation Vectors
Jan 10, 2025



Abstract:As large language models (LLMs) are widely deployed across various domains, the ability to control their generated outputs has become more critical. This control involves aligning LLMs outputs with human values and ethical principles or customizing LLMs on specific topics or styles for individual users. Existing controlled generation methods either require significant computational resources and extensive trial-and-error or provide coarse-grained control. In this paper, we propose Generation with Concept Activation Vector (GCAV), a lightweight model control framework that ensures accurate control without requiring resource-extensive fine-tuning. Specifically, GCAV first trains a concept activation vector for specified concepts to be controlled, such as toxicity. During inference, GCAV steers the concept vector in LLMs, for example, by removing the toxicity concept vector from the activation layers. Control experiments from different perspectives, including toxicity reduction, sentiment control, linguistic style, and topic control, demonstrate that our framework achieves state-of-the-art performance with granular control, allowing for fine-grained adjustments of both the steering layers and the steering magnitudes for individual samples.
Baichuan4-Finance Technical Report
Dec 17, 2024



Abstract:Large language models (LLMs) have demonstrated strong capabilities in language understanding, generation, and reasoning, yet their potential in finance remains underexplored due to the complexity and specialization of financial knowledge. In this work, we report the development of the Baichuan4-Finance series, including a comprehensive suite of foundational Baichuan4-Finance-Base and an aligned language model Baichuan4-Finance, which are built upon Baichuan4-Turbo base model and tailored for finance domain. Firstly, we have dedicated significant effort to building a detailed pipeline for improving data quality. Moreover, in the continual pre-training phase, we propose a novel domain self-constraint training strategy, which enables Baichuan4-Finance-Base to acquire financial knowledge without losing general capabilities. After Supervised Fine-tuning and Reinforcement Learning from Human Feedback and AI Feedback, the chat model Baichuan4-Finance is able to tackle various financial certification questions and real-world scenario applications. We evaluate Baichuan4-Finance on many widely used general datasets and two holistic financial benchmarks. The evaluation results show that Baichuan4-Finance-Base surpasses almost all competitive baselines on financial tasks by significant margins without sacrificing performance on general LLM benchmarks. At the same time, Baichuan4-Finance demonstrates even more impressive performance on financial application scenarios, showcasing its potential to foster community innovation in the financial LLM field.
LLMForecaster: Improving Seasonal Event Forecasts with Unstructured Textual Data
Dec 03, 2024



Abstract:Modern time-series forecasting models often fail to make full use of rich unstructured information about the time series themselves. This lack of proper conditioning can lead to obvious model failures; for example, models may be unaware of the details of a particular product, and hence fail to anticipate seasonal surges in customer demand in the lead up to major exogenous events like holidays for clearly relevant products. To address this shortcoming, this paper introduces a novel forecast post-processor -- which we call LLMForecaster -- that fine-tunes large language models (LLMs) to incorporate unstructured semantic and contextual information and historical data to improve the forecasts from an existing demand forecasting pipeline. In an industry-scale retail application, we demonstrate that our technique yields statistically significantly forecast improvements across several sets of products subject to holiday-driven demand surges.
Weather-Informed Probabilistic Forecasting and Scenario Generation in Power Systems
Sep 11, 2024



Abstract:The integration of renewable energy sources (RES) into power grids presents significant challenges due to their intrinsic stochasticity and uncertainty, necessitating the development of new techniques for reliable and efficient forecasting. This paper proposes a method combining probabilistic forecasting and Gaussian copula for day-ahead prediction and scenario generation of load, wind, and solar power in high-dimensional contexts. By incorporating weather covariates and restoring spatio-temporal correlations, the proposed method enhances the reliability of probabilistic forecasts in RES. Extensive numerical experiments compare the effectiveness of different time series models, with performance evaluated using comprehensive metrics on a real-world and high-dimensional dataset from Midcontinent Independent System Operator (MISO). The results highlight the importance of weather information and demonstrate the efficacy of the Gaussian copula in generating realistic scenarios, with the proposed weather-informed Temporal Fusion Transformer (WI-TFT) model showing superior performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge