Uncertainty-Aware Delivery Delay Duration Prediction via Multi-Task Deep Learning

Accurate delivery delay prediction is critical for maintaining operational efficiency and customer satisfaction across modern supply chains. Yet the increasing complexity of logistics networks, spanning multimodal transportation, cross-country routing, and pronounced regional variability, makes this prediction task inherently challenging. This paper introduces a multi-task deep learning model for delivery delay duration prediction in the presence of significant imbalanced data, where delayed shipments are rare but operationally consequential. The model embeds high-dimensional shipment features with dedicated embedding layers for tabular data, and then uses a classification-then-regression strategy to predict the delivery delay duration for on-time and delayed shipments. Unlike sequential pipelines, this approach enables end-to-end training, improves the detection of delayed cases, and supports probabilistic forecasting for uncertainty-aware decision making. The proposed approach is evaluated on a large-scale real-world dataset from an industrial partner, comprising more than 10 million historical shipment records across four major source locations with distinct regional characteristics. The proposed model is compared with traditional machine learning methods. Experimental results show that the proposed method achieves a mean absolute error of 0.67-0.91 days for delayed-shipment predictions, outperforming single-step tree-based regression baselines by 41-64% and two-step classify-then-regress tree-based models by 15-35%. These gains demonstrate the effectiveness of the proposed model in operational delivery delay forecasting under highly imbalanced and heterogeneous conditions.

Copula-Based Aggregation and Context-Aware Conformal Prediction for Reliable Renewable Energy Forecasting

The rapid growth of renewable energy penetration has intensified the need for reliable probabilistic forecasts to support grid operations at aggregated (fleet or system) levels. In practice, however, system operators often lack access to fleet-level probabilistic models and instead rely on site-level forecasts produced by heterogeneous third-party providers. Constructing coherent and calibrated fleet-level probabilistic forecasts from such inputs remains challenging due to complex cross-site dependencies and aggregation-induced miscalibration. This paper proposes a calibrated probabilistic aggregation framework that directly converts site-level probabilistic forecasts into reliable fleet-level forecasts in settings where system-level models cannot be trained or maintained. The framework integrates copula-based dependence modeling to capture cross-site correlations with Context-Aware Conformal Prediction (CACP) to correct miscalibration at the aggregated level. This combination enables dependence-aware aggregation while providing valid coverage and maintaining sharp prediction intervals. Experiments on large-scale solar generation datasets from MISO, ERCOT, and SPP demonstrate that the proposed Copula+CACP approach consistently achieves near-nominal coverage with significantly sharper intervals than uncalibrated aggregation baselines.

A Rolling-Space Branch-and-Price Algorithm for the Multi-Compartment Vehicle Routing Problem with Multiple Time Windows

This paper investigates the multi-compartment vehicle routing problem with multiple time windows (MCVRPMTW), an extension of the classical vehicle routing problem with time windows that considers vehicles equipped with multiple compartments and customers requiring service across several delivery time windows. The problem incorporates three key compartment-related features: (i) compartment flexibility in the number of compartments, (ii) item-to-compartment compatibility, and (iii) item-to-item compatibility. The problem also accommodates practical operational requirements such as driver breaks. To solve the MCVRPMTW, we develop an exact branch-and-price (B&P) algorithm in which the pricing problem is solved using a labeling algorithm. Several acceleration strategies are introduced to limit symmetry during label extensions, improve the stability of dual solutions in column generation, and enhance the branching process. To handle large-scale instances, we propose a rolling-space B&P algorithm that integrates clustering techniques into the solution framework. Extensive computational experiments on instances inspired by a real-world industrial application demonstrate the effectiveness of the proposed approach and provide useful managerial insights for practical implementation.

Plan, Verify and Fill: A Structured Parallel Decoding Approach for Diffusion Language Models

Diffusion Language Models (DLMs) present a promising non-sequential paradigm for text generation, distinct from standard autoregressive (AR) approaches. However, current decoding strategies often adopt a reactive stance, underutilizing the global bidirectional context to dictate global trajectories. To address this, we propose Plan-Verify-Fill (PVF), a training-free paradigm that grounds planning via quantitative validation. PVF actively constructs a hierarchical skeleton by prioritizing high-leverage semantic anchors and employs a verification protocol to operationalize pragmatic structural stopping where further deliberation yields diminishing returns. Extensive evaluations on LLaDA-8B-Instruct and Dream-7B-Instruct demonstrate that PVF reduces the Number of Function Evaluations (NFE) by up to 65% compared to confidence-based parallel decoding across benchmark datasets, unlocking superior efficiency without compromising accuracy.

ID-PaS : Identity-Aware Predict-and-Search for General Mixed-Integer Linear Programs

Mixed-Integer Linear Programs (MIPs) are powerful and flexible tools for modeling a wide range of real-world combinatorial optimization problems. Predict-and-Search methods operate by using a predictive model to estimate promising variable assignments and then guiding a search procedure toward high-quality solutions. Recent research has demonstrated that incorporating machine learning (ML) into the Predict-and-Search framework significantly enhances its performance. Still, it is restricted to binary problems and overlooks the presence of fixed variables that commonly arise in practical settings. This work extends the Predict-and-Search (PaS) framework to parametric MIPs and introduces ID-PaS, an identity-aware learning framework that enables the ML model to handle heterogeneous variables more effectively. Experiments on several real-world large-scale problems demonstrate that ID-PaS consistently achieves superior performance compared to the state-of-the-art solver Gurobi and PaS.

Constraint-Informed Active Learning for End-to-End ACOPF Optimization Proxies

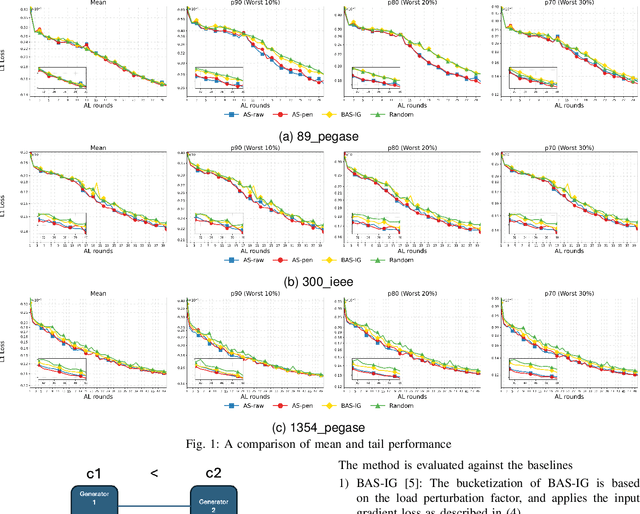
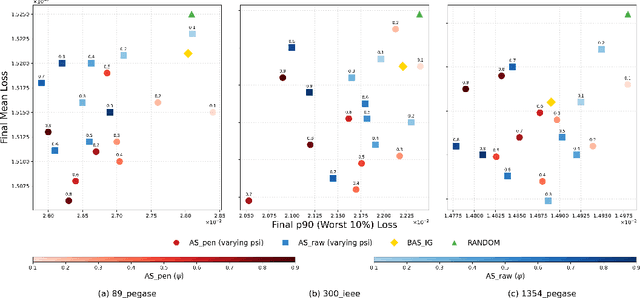
This paper studies optimization proxies, machine learning (ML) models trained to efficiently predict optimal solutions for AC Optimal Power Flow (ACOPF) problems. While promising, optimization proxy performance heavily depends on training data quality. To address this limitation, this paper introduces a novel active sampling framework for ACOPF optimization proxies designed to generate realistic and diverse training data. The framework actively explores varied, flexible problem specifications reflecting plausible operational realities. More importantly, the approach uses optimization-specific quantities (active constraint sets) that better capture the salient features of an ACOPF that lead to the optimal solution. Numerical results show superior generalization over existing sampling methods with an equivalent training budget, significantly advancing the state-of-practice for trustworthy ACOPF optimization proxies.

A General and Streamlined Differentiable Optimization Framework

Differentiating through constrained optimization problems is increasingly central to learning, control, and large-scale decision-making systems, yet practical integration remains challenging due to solver specialization and interface mismatches. This paper presents a general and streamlined framework-an updated DiffOpt.jl-that unifies modeling and differentiation within the Julia optimization stack. The framework computes forward - and reverse-mode solution and objective sensitivities for smooth, potentially nonconvex programs by differentiating the KKT system under standard regularity assumptions. A first-class, JuMP-native parameter-centric API allows users to declare named parameters and obtain derivatives directly with respect to them - even when a parameter appears in multiple constraints and objectives - eliminating brittle bookkeeping from coefficient-level interfaces. We illustrate these capabilities on convex and nonconvex models, including economic dispatch, mean-variance portfolio selection with conic risk constraints, and nonlinear robot inverse kinematics. Two companion studies further demonstrate impact at scale: gradient-based iterative methods for strategic bidding in energy markets and Sobolev-style training of end-to-end optimization proxies using solver-accurate sensitivities. Together, these results demonstrate that differentiable optimization can be deployed as a routine tool for experimentation, learning, calibration, and design-without deviating from standard JuMP modeling practices and while retaining access to a broad ecosystem of solvers.

Sequence Variables: A Constraint Programming Computational Domain for Routing and Sequencing

Constraint Programming (CP) offers an intuitive, declarative framework for modeling Vehicle Routing Problems (VRP), yet classical CP models based on successor variables cannot always deal with optional visits or insertion based heuristics. To address these limitations, this paper formalizes sequence variables within CP. Unlike the classical successor models, this computational domain handle optional visits and support insertion heuristics, including insertion-based Large Neighborhood Search. We provide a clear definition of their domain, update operations, and introduce consistency levels for constraints on this domain. An implementation is described with the underlying data structures required for integrating sequence variables into existing trail-based CP solvers. Furthermore, global constraints specifically designed for sequence variables and vehicle routing are introduced. Finally, the effectiveness of sequence variables is demonstrated by simplifying problem modeling and achieving competitive computational performance on the Dial-a-Ride Problem.

PGLearn -- An Open-Source Learning Toolkit for Optimal Power Flow

Machine Learning (ML) techniques for Optimal Power Flow (OPF) problems have recently garnered significant attention, reflecting a broader trend of leveraging ML to approximate and/or accelerate the resolution of complex optimization problems. These developments are necessitated by the increased volatility and scale in energy production for modern and future grids. However, progress in ML for OPF is hindered by the lack of standardized datasets and evaluation metrics, from generating and solving OPF instances, to training and benchmarking machine learning models. To address this challenge, this paper introduces PGLearn, a comprehensive suite of standardized datasets and evaluation tools for ML and OPF. PGLearn provides datasets that are representative of real-life operating conditions, by explicitly capturing both global and local variability in the data generation, and by, for the first time, including time series data for several large-scale systems. In addition, it supports multiple OPF formulations, including AC, DC, and second-order cone formulations. Standardized datasets are made publicly available to democratize access to this field, reduce the burden of data generation, and enable the fair comparison of various methodologies. PGLearn also includes a robust toolkit for training, evaluating, and benchmarking machine learning models for OPF, with the goal of standardizing performance evaluation across the field. By promoting open, standardized datasets and evaluation metrics, PGLearn aims at democratizing and accelerating research and innovation in machine learning applications for optimal power flow problems. Datasets are available for download at https://www.huggingface.co/PGLearn.

DualSchool: How Reliable are LLMs for Optimization Education?

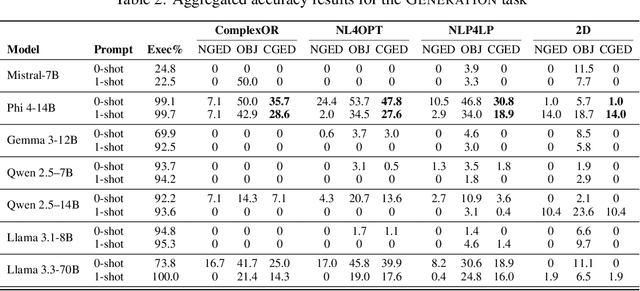
Consider the following task taught in introductory optimization courses which addresses challenges articulated by the community at the intersection of (generative) AI and OR: generate the dual of a linear program. LLMs, being trained at web-scale, have the conversion process and many instances of Primal to Dual Conversion (P2DC) at their disposal. Students may thus reasonably expect that LLMs would perform well on the P2DC task. To assess this expectation, this paper introduces DualSchool, a comprehensive framework for generating and verifying P2DC instances. The verification procedure of DualSchool uses the Canonical Graph Edit Distance, going well beyond existing evaluation methods for optimization models, which exhibit many false positives and negatives when applied to P2DC. Experiments performed by DualSchool reveal interesting findings. Although LLMs can recite the conversion procedure accurately, state-of-the-art open LLMs fail to consistently produce correct duals. This finding holds even for the smallest two-variable instances and for derivative tasks, such as correctness, verification, and error classification. The paper also discusses the implications for educators, students, and the development of large reasoning systems.