Factor Importance Ranking and Selection using Total Indices

Factor importance measures the impact of each feature on output prediction accuracy. Many existing works focus on the model-based importance, but an important feature in one learning algorithm may hold little significance in another model. Hence, a factor importance measure ought to characterize the feature's predictive potential without relying on a specific prediction algorithm. Such algorithm-agnostic importance is termed as intrinsic importance in Williamson et al. (2023), but their estimator again requires model fitting. To bypass the modeling step, we present the equivalence between predictiveness potential and total Sobol' indices from global sensitivity analysis, and introduce a novel consistent estimator that can be directly estimated from noisy data. Integrating with forward selection and backward elimination gives rise to FIRST, Factor Importance Ranking and Selection using Total (Sobol') indices. Extensive simulations are provided to demonstrate the effectiveness of FIRST on regression and binary classification problems, and a clear advantage over the state-of-the-art methods.

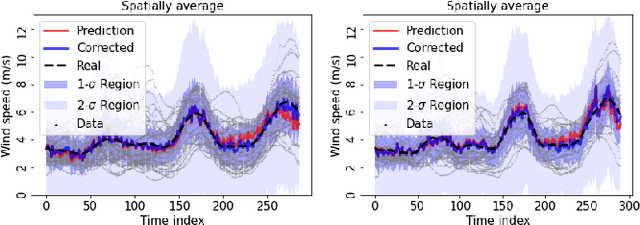
Asset Bundling for Wind Power Forecasting

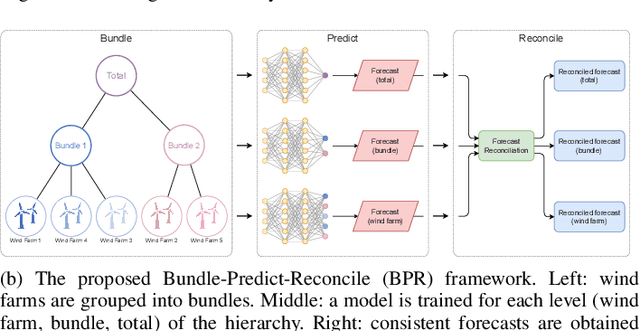
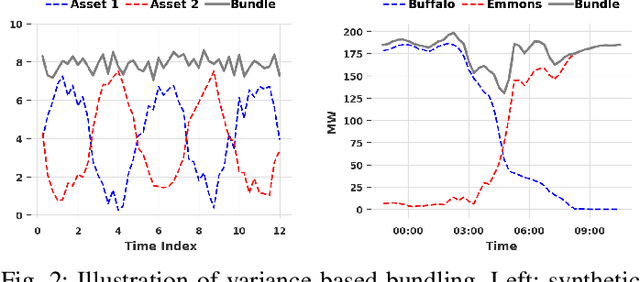
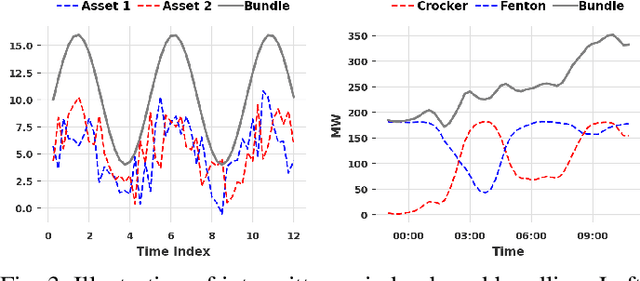
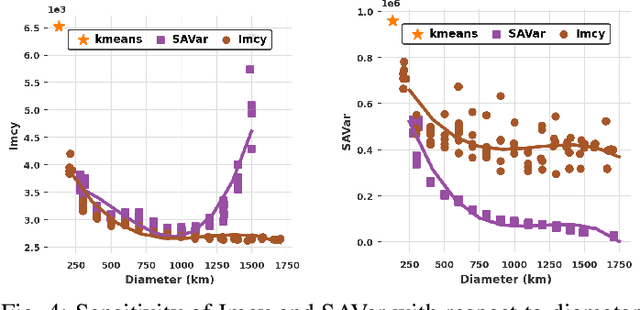
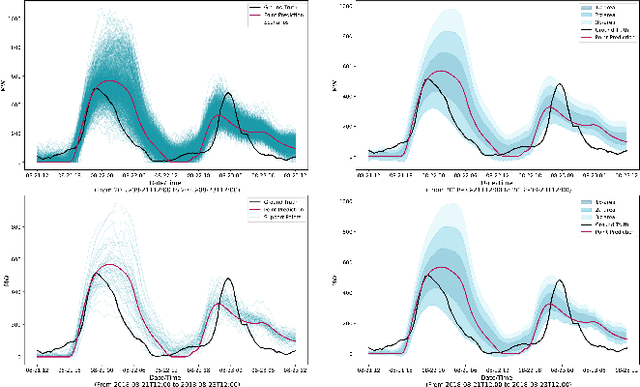
The growing penetration of intermittent, renewable generation in US power grids, especially wind and solar generation, results in increased operational uncertainty. In that context, accurate forecasts are critical, especially for wind generation, which exhibits large variability and is historically harder to predict. To overcome this challenge, this work proposes a novel Bundle-Predict-Reconcile (BPR) framework that integrates asset bundling, machine learning, and forecast reconciliation techniques. The BPR framework first learns an intermediate hierarchy level (the bundles), then predicts wind power at the asset, bundle, and fleet level, and finally reconciles all forecasts to ensure consistency. This approach effectively introduces an auxiliary learning task (predicting the bundle-level time series) to help the main learning tasks. The paper also introduces new asset-bundling criteria that capture the spatio-temporal dynamics of wind power time series. Extensive numerical experiments are conducted on an industry-size dataset of 283 wind farms in the MISO footprint. The experiments consider short-term and day-ahead forecasts, and evaluates a large variety of forecasting models that include weather predictions as covariates. The results demonstrate the benefits of BPR, which consistently and significantly improves forecast accuracy over baselines, especially at the fleet level.

Optimal Sub-sampling to Boost Power of Kernel Sequential Change-point Detection

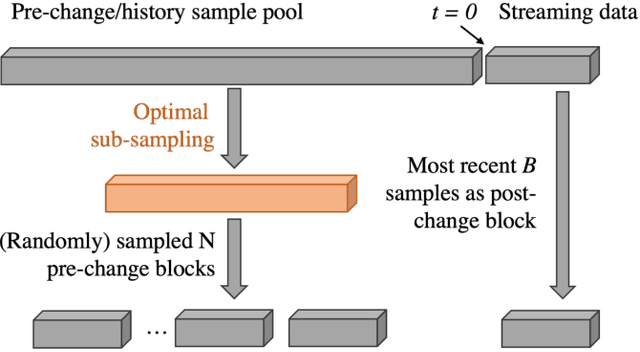
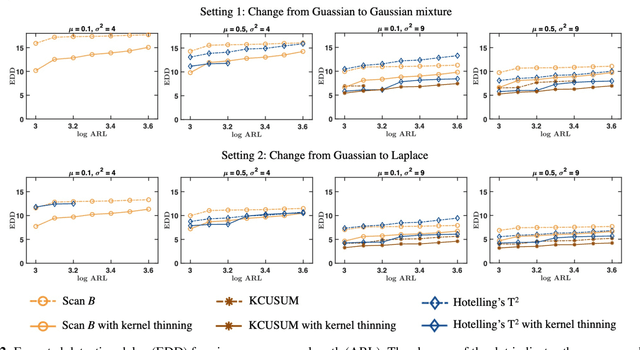
We present a novel scheme to boost detection power for kernel maximum mean discrepancy based sequential change-point detection procedures. Our proposed scheme features an optimal sub-sampling of the history data before the detection procedure, in order to tackle the power loss incurred by the random sub-sample from the enormous history data. We apply our proposed scheme to both Scan $B$ and Kernel Cumulative Sum (CUSUM) procedures, and improved performance is observed from extensive numerical experiments.

Risk-Aware Control and Optimization for High-Renewable Power Grids

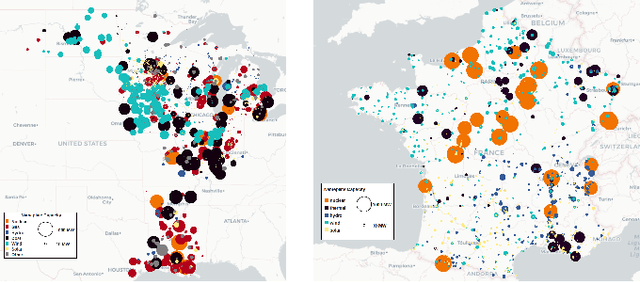
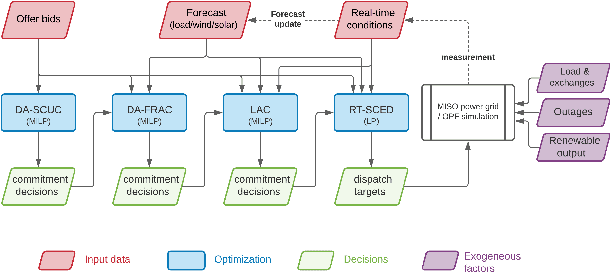
The transition of the electrical power grid from fossil fuels to renewable sources of energy raises fundamental challenges to the market-clearing algorithms that drive its operations. Indeed, the increased stochasticity in load and the volatility of renewable energy sources have led to significant increases in prediction errors, affecting the reliability and efficiency of existing deterministic optimization models. The RAMC project was initiated to investigate how to move from this deterministic setting into a risk-aware framework where uncertainty is quantified explicitly and incorporated in the market-clearing optimizations. Risk-aware market-clearing raises challenges on its own, primarily from a computational standpoint. This paper reviews how RAMC approaches risk-aware market clearing and presents some of its innovations in uncertainty quantification, optimization, and machine learning. Experimental results on real networks are presented.

MAGI-X: Manifold-Constrained Gaussian Process Inference for Unknown System Dynamics

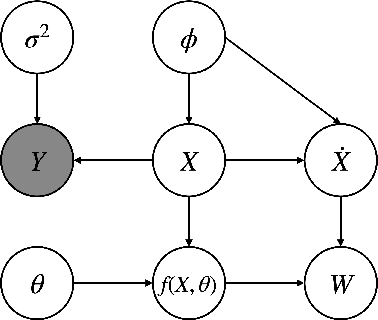
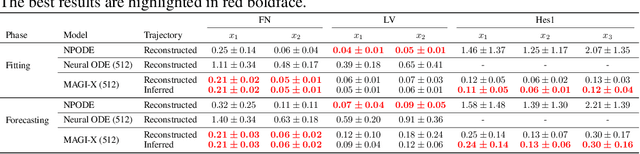
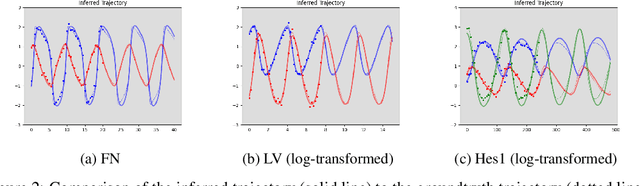
Ordinary differential equations (ODEs), commonly used to characterize the dynamic systems, are difficult to propose in closed-form for many complicated scientific applications, even with the help of domain expert. We propose a fast and accurate data-driven method, MAGI-X, to learn the unknown dynamic from the observation data in a non-parametric fashion, without the need of any domain knowledge. Unlike the existing methods that mainly rely on the costly numerical integration, MAGI-X utilizes the powerful functional approximator of neural network to learn the unknown nonlinear dynamic within the MAnifold-constrained Gaussian process Inference (MAGI) framework that completely circumvents the numerical integration. Comparing against the state-of-the-art methods on three realistic examples, MAGI-X achieves competitive accuracy in both fitting and forecasting while only taking a fraction of computational time. Moreover, MAGI-X provides practical solution for the inference of partial observed systems, which no previous method is able to handle.

An Infinite Hidden Markov Model With Similarity-Biased Transitions

We describe a generalization of the Hierarchical Dirichlet Process Hidden Markov Model (HDP-HMM) which is able to encode prior information that state transitions are more likely between "nearby" states. This is accomplished by defining a similarity function on the state space and scaling transition probabilities by pair-wise similarities, thereby inducing correlations among the transition distributions. We present an augmented data representation of the model as a Markov Jump Process in which: (1) some jump attempts fail, and (2) the probability of success is proportional to the similarity between the source and destination states. This augmentation restores conditional conjugacy and admits a simple Gibbs sampler. We evaluate the model and inference method on a speaker diarization task and a "harmonic parsing" task using four-part chorale data, as well as on several synthetic datasets, achieving favorable comparisons to existing models.