A Global-Local Approximation Framework for Large-Scale Gaussian Process Modeling

In this work, we propose a novel framework for large-scale Gaussian process (GP) modeling. Contrary to the global, and local approximations proposed in the literature to address the computational bottleneck with exact GP modeling, we employ a combined global-local approach in building the approximation. Our framework uses a subset-of-data approach where the subset is a union of a set of global points designed to capture the global trend in the data, and a set of local points specific to a given testing location to capture the local trend around the testing location. The correlation function is also modeled as a combination of a global, and a local kernel. The performance of our framework, which we refer to as TwinGP, is on par or better than the state-of-the-art GP modeling methods at a fraction of their computational cost.

Risk-Aware Control and Optimization for High-Renewable Power Grids

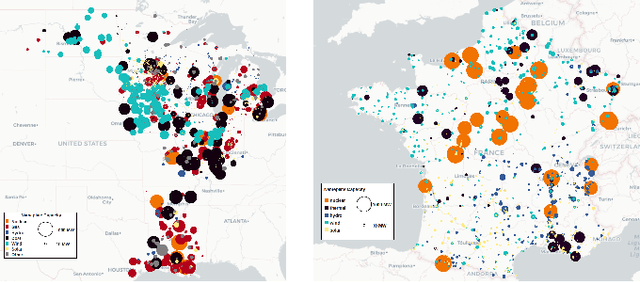
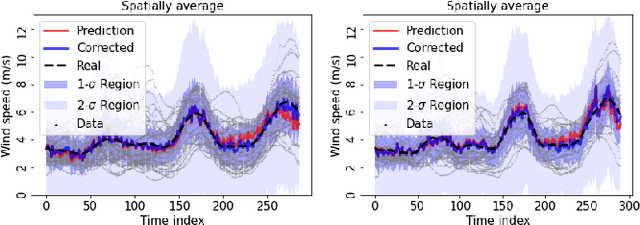
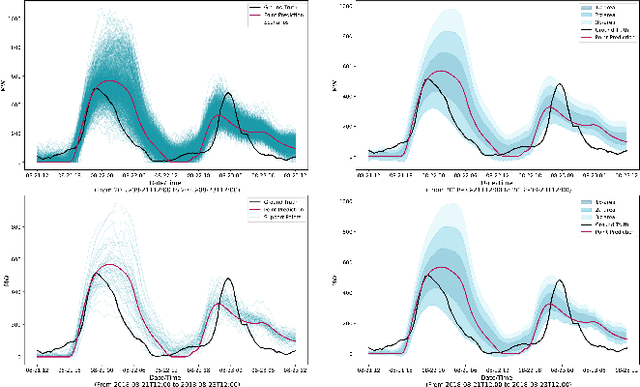
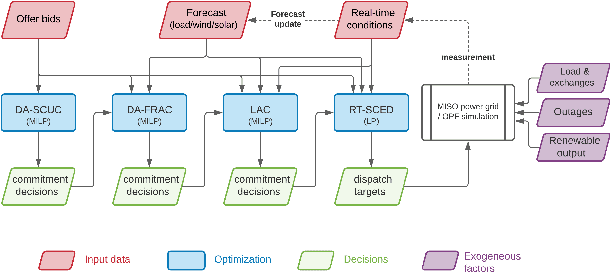
The transition of the electrical power grid from fossil fuels to renewable sources of energy raises fundamental challenges to the market-clearing algorithms that drive its operations. Indeed, the increased stochasticity in load and the volatility of renewable energy sources have led to significant increases in prediction errors, affecting the reliability and efficiency of existing deterministic optimization models. The RAMC project was initiated to investigate how to move from this deterministic setting into a risk-aware framework where uncertainty is quantified explicitly and incorporated in the market-clearing optimizations. Risk-aware market-clearing raises challenges on its own, primarily from a computational standpoint. This paper reviews how RAMC approaches risk-aware market clearing and presents some of its innovations in uncertainty quantification, optimization, and machine learning. Experimental results on real networks are presented.

Distributional Clustering: A distribution-preserving clustering method

One key use of k-means clustering is to identify cluster prototypes which can serve as representative points for a dataset. However, a drawback of using k-means cluster centers as representative points is that such points distort the distribution of the underlying data. This can be highly disadvantageous in problems where the representative points are subsequently used to gain insights on the data distribution, as these points do not mimic the distribution of the data. To this end, we propose a new clustering method called "distributional clustering", which ensures cluster centers capture the distribution of the underlying data. We first prove the asymptotic convergence of the proposed cluster centers to the data generating distribution, then present an efficient algorithm for computing these cluster centers in practice. Finally, we demonstrate the effectiveness of distributional clustering on synthetic and real datasets.