Self-Supervised Learning for Large-Scale Preventive Security Constrained DC Optimal Power Flow

Security-Constrained Optimal Power Flow (SCOPF) plays a crucial role in power grid stability but becomes increasingly complex as systems grow. This paper introduces PDL-SCOPF, a self-supervised end-to-end primal-dual learning framework for producing near-optimal solutions to large-scale SCOPF problems in milliseconds. Indeed, PDL-SCOPF remedies the limitations of supervised counterparts that rely on training instances with their optimal solutions, which becomes impractical for large-scale SCOPF problems. PDL-SCOPF mimics an Augmented Lagrangian Method (ALM) for training primal and dual networks that learn the primal solutions and the Lagrangian multipliers, respectively, to the unconstrained optimizations. In addition, PDL-SCOPF incorporates a repair layer to ensure the feasibility of the power balance in the nominal case, and a binary search layer to compute, using the Automatic Primary Response (APR), the generator dispatches in the contingencies. The resulting differentiable program can then be trained end-to-end using the objective function of the SCOPF and the power balance constraints of the contingencies. Experimental results demonstrate that the PDL-SCOPF delivers accurate feasible solutions with minimal optimality gaps. The framework underlying PDL-SCOPF aims at bridging the gap between traditional optimization methods and machine learning, highlighting the potential of self-supervised end-to-end primal-dual learning for large-scale optimization tasks.

Compact Optimization Learning for AC Optimal Power Flow

This paper reconsiders end-to-end learning approaches to the Optimal Power Flow (OPF). Existing methods, which learn the input/output mapping of the OPF, suffer from scalability issues due to the high dimensionality of the output space. This paper first shows that the space of optimal solutions can be significantly compressed using principal component analysis (PCA). It then proposes Compact Learning, a new method that learns in a subspace of the principal components before translating the vectors into the original output space. This compression reduces the number of trainable parameters substantially, improving scalability and effectiveness. Compact Learning is evaluated on a variety of test cases from the PGLib with up to 30,000 buses. The paper also shows that the output of Compact Learning can be used to warm-start an exact AC solver to restore feasibility, while bringing significant speed-ups.

Confidence-Aware Graph Neural Networks for Learning Reliability Assessment Commitments

Reliability Assessment Commitment (RAC) Optimization is increasingly important in grid operations due to larger shares of renewable generations in the generation mix and increased prediction errors. Independent System Operators (ISOs) also aim at using finer time granularities, longer time horizons, and possibly stochastic formulations for additional economic and reliability benefits. The goal of this paper is to address the computational challenges arising in extending the scope of RAC formulations. It presents RACLEARN that (1) uses Graph Neural Networks (GNN) to predict generator commitments and active line constraints, (2) associates a confidence value to each commitment prediction, (3) selects a subset of the high-confidence predictions, which are (4) repaired for feasibility, and (5) seeds a state-of-the-art optimization algorithm with the feasible predictions and the active constraints. Experimental results on exact RAC formulations used by the Midcontinent Independent System Operator (MISO) and an actual transmission network (8965 transmission lines, 6708 buses, 1890 generators, and 6262 load units) show that the RACLEARN framework can speed up RAC optimization by factors ranging from 2 to 4 with negligible loss in solution quality.

Self-Supervised Primal-Dual Learning for Constrained Optimization

This paper studies how to train machine-learning models that directly approximate the optimal solutions of constrained optimization problems. This is an empirical risk minimization under constraints, which is challenging as training must balance optimality and feasibility conditions. Supervised learning methods often approach this challenge by training the model on a large collection of pre-solved instances. This paper takes a different route and proposes the idea of Primal-Dual Learning (PDL), a self-supervised training method that does not require a set of pre-solved instances or an optimization solver for training and inference. Instead, PDL mimics the trajectory of an Augmented Lagrangian Method (ALM) and jointly trains primal and dual neural networks. Being a primal-dual method, PDL uses instance-specific penalties of the constraint terms in the loss function used to train the primal network. Experiments show that, on a set of nonlinear optimization benchmarks, PDL typically exhibits negligible constraint violations and minor optimality gaps, and is remarkably close to the ALM optimization. PDL also demonstrated improved or similar performance in terms of the optimality gaps, constraint violations, and training times compared to existing approaches.

Risk-Aware Control and Optimization for High-Renewable Power Grids

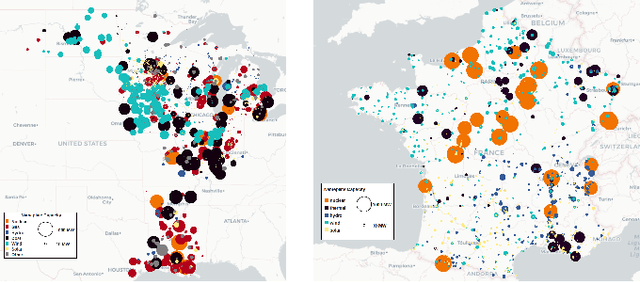
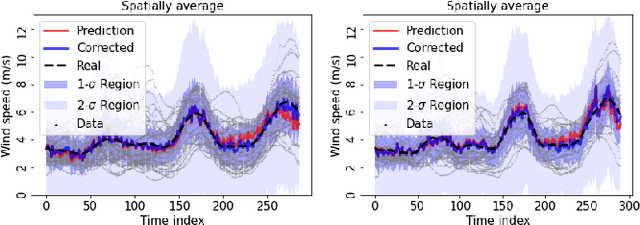
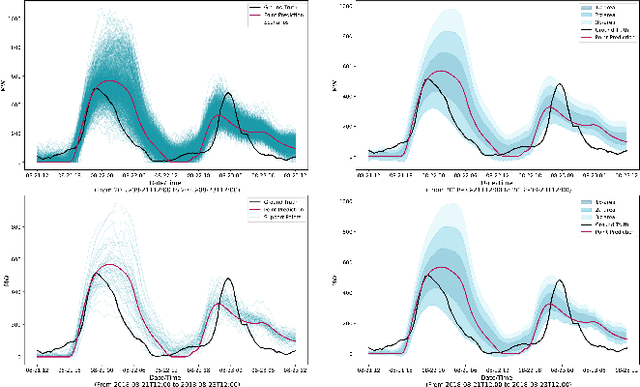
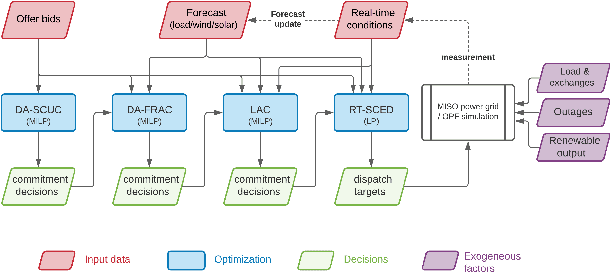
The transition of the electrical power grid from fossil fuels to renewable sources of energy raises fundamental challenges to the market-clearing algorithms that drive its operations. Indeed, the increased stochasticity in load and the volatility of renewable energy sources have led to significant increases in prediction errors, affecting the reliability and efficiency of existing deterministic optimization models. The RAMC project was initiated to investigate how to move from this deterministic setting into a risk-aware framework where uncertainty is quantified explicitly and incorporated in the market-clearing optimizations. Risk-aware market-clearing raises challenges on its own, primarily from a computational standpoint. This paper reviews how RAMC approaches risk-aware market clearing and presents some of its innovations in uncertainty quantification, optimization, and machine learning. Experimental results on real networks are presented.

Learning Optimization Proxies for Large-Scale Security-Constrained Economic Dispatch

The Security-Constrained Economic Dispatch (SCED) is a fundamental optimization model for Transmission System Operators (TSO) to clear real-time energy markets while ensuring reliable operations of power grids. In a context of growing operational uncertainty, due to increased penetration of renewable generators and distributed energy resources, operators must continuously monitor risk in real-time, i.e., they must quickly assess the system's behavior under various changes in load and renewable production. Unfortunately, systematically solving an optimization problem for each such scenario is not practical given the tight constraints of real-time operations. To overcome this limitation, this paper proposes to learn an optimization proxy for SCED, i.e., a Machine Learning (ML) model that can predict an optimal solution for SCED in milliseconds. Motivated by a principled analysis of the market-clearing optimizations of MISO, the paper proposes a novel ML pipeline that addresses the main challenges of learning SCED solutions, i.e., the variability in load, renewable output and production costs, as well as the combinatorial structure of commitment decisions. A novel Classification-Then-Regression architecture is also proposed, to further capture the behavior of SCED solutions. Numerical experiments are reported on the French transmission system, and demonstrate the approach's ability to produce, within a time frame that is compatible with real-time operations, accurate optimization proxies that produce relative errors below $0.6\%$.

Homography augumented momentum constrastive learning for SAR image retrieval

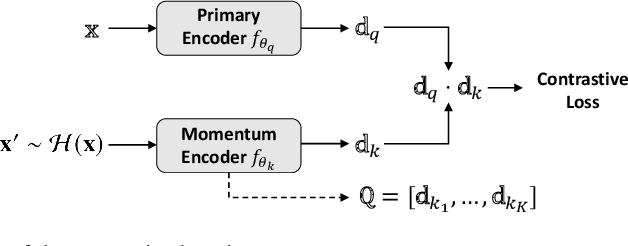
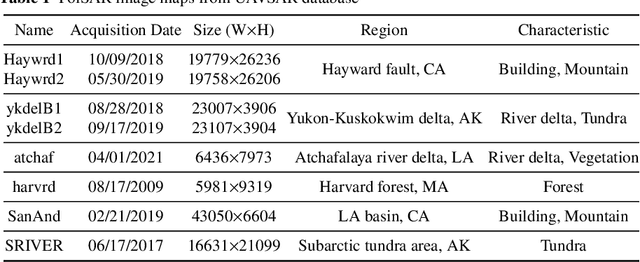
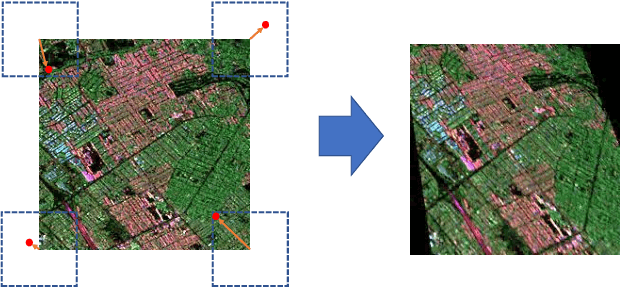
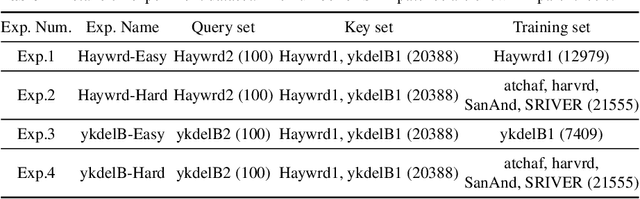
Deep learning-based image retrieval has been emphasized in computer vision. Representation embedding extracted by deep neural networks (DNNs) not only aims at containing semantic information of the image, but also can manage large-scale image retrieval tasks. In this work, we propose a deep learning-based image retrieval approach using homography transformation augmented contrastive learning to perform large-scale synthetic aperture radar (SAR) image search tasks. Moreover, we propose a training method for the DNNs induced by contrastive learning that does not require any labeling procedure. This may enable tractability of large-scale datasets with relative ease. Finally, we verify the performance of the proposed method by conducting experiments on the polarimetric SAR image datasets.

Deep Data Density Estimation through Donsker-Varadhan Representation

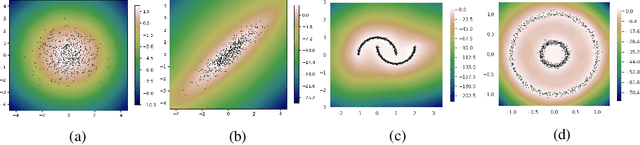
Estimating the data density is one of the challenging problems in deep learning. In this paper, we present a simple yet effective method for estimating the data density using a deep neural network and the Donsker-Varadhan variational lower bound on the KL divergence. We show that the optimal critic function associated with the Donsker-Varadhan representation on the KL divergence between the data and the uniform distribution can estimate the data density. We also present the deep neural network-based modeling and its stochastic learning. The experimental results and possible applications of the proposed method demonstrate that it is competitive with the previous methods and has a lot of possibilities in applied to various applications.

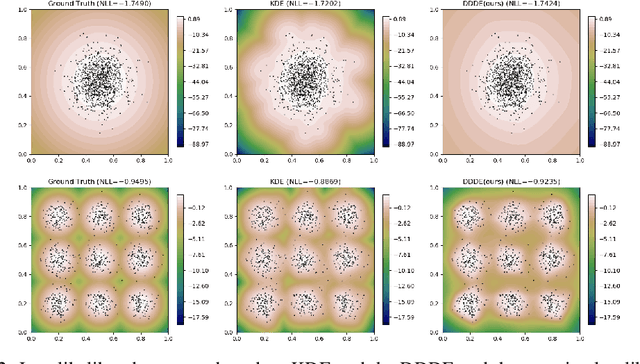
Interpreting Rate-Distortion of Variational Autoencoder and Using Model Uncertainty for Anomaly Detection

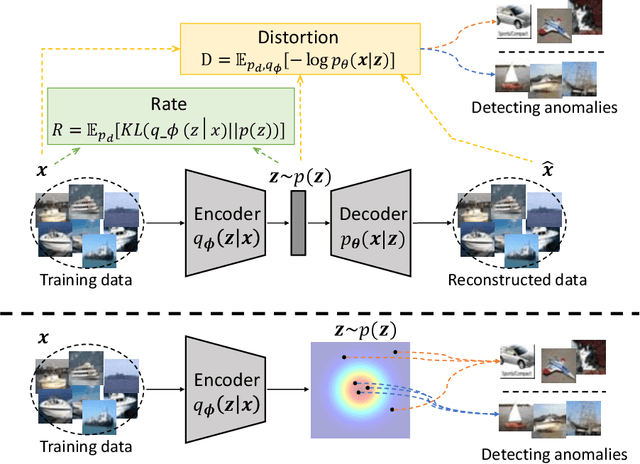
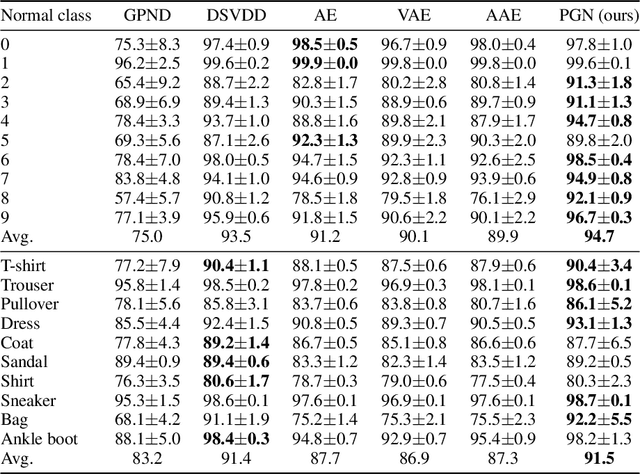
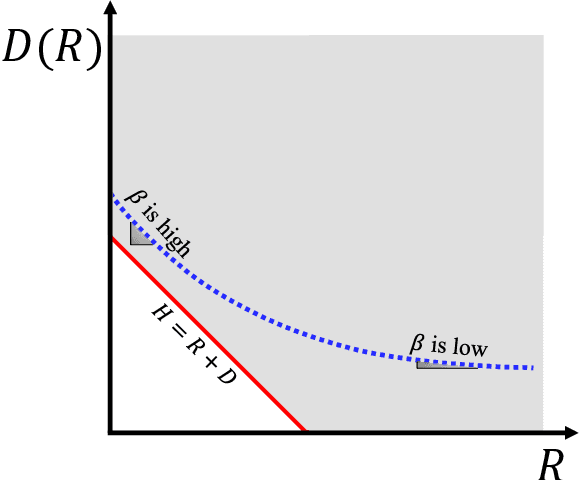
Building a scalable machine learning system for unsupervised anomaly detection via representation learning is highly desirable. One of the prevalent methods is using a reconstruction error from variational autoencoder (VAE) via maximizing the evidence lower bound. We revisit VAE from the perspective of information theory to provide some theoretical foundations on using the reconstruction error, and finally arrive at a simpler and more effective model for anomaly detection. In addition, to enhance the effectiveness of detecting anomalies, we incorporate a practical model uncertainty measure into the metric. We show empirically the competitive performance of our approach on benchmark datasets.

Combining Stochastic Adaptive Cubic Regularization with Negative Curvature for Nonconvex Optimization

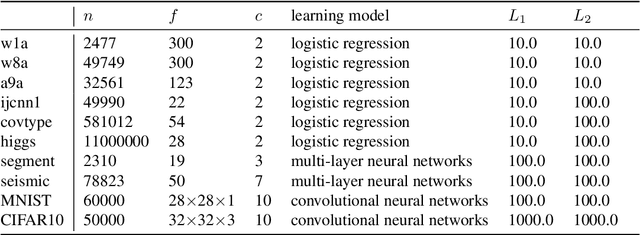
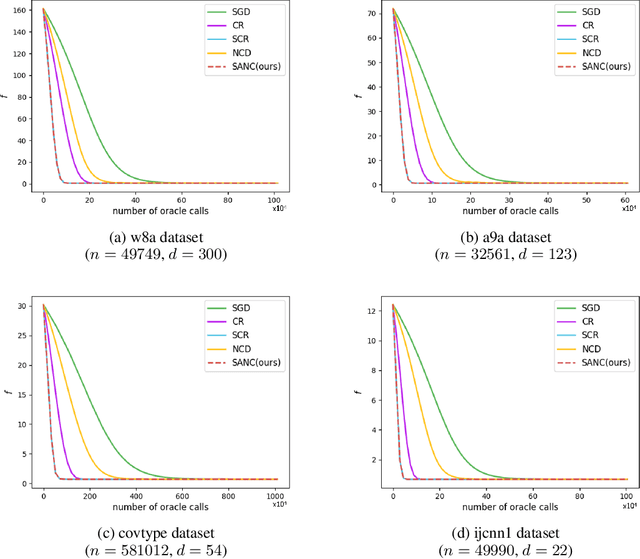
We focus on minimizing nonconvex finite-sum functions that typically arise in machine learning problems. In an attempt to solve this problem, the adaptive cubic regularized Newton method has shown its strong global convergence guarantees and ability to escape from strict saddle points. This method uses a trust region-like scheme to determine if an iteration is successful or not, and updates only when it is successful. In this paper, we suggest an algorithm combining negative curvature with the adaptive cubic regularized Newton method to update even at unsuccessful iterations. We call this new method Stochastic Adaptive cubic regularization with Negative Curvature (SANC). Unlike the previous method, in order to attain stochastic gradient and Hessian estimators, the SANC algorithm uses independent sets of data points of consistent size over all iterations. It makes the SANC algorithm more practical to apply for solving large-scale machine learning problems. To the best of our knowledge, this is the first approach that combines the negative curvature method with the adaptive cubic regularized Newton method. Finally, we provide experimental results including neural networks problems supporting the efficiency of our method.