A Brief Review of Explainable Artificial Intelligence in Healthcare

XAI refers to the techniques and methods for building AI applications which assist end users to interpret output and predictions of AI models. Black box AI applications in high-stakes decision-making situations, such as medical domain have increased the demand for transparency and explainability since wrong predictions may have severe consequences. Model explainability and interpretability are vital successful deployment of AI models in healthcare practices. AI applications' underlying reasoning needs to be transparent to clinicians in order to gain their trust. This paper presents a systematic review of XAI aspects and challenges in the healthcare domain. The primary goals of this study are to review various XAI methods, their challenges, and related machine learning models in healthcare. The methods are discussed under six categories: Features-oriented methods, global methods, concept models, surrogate models, local pixel-based methods, and human-centric methods. Most importantly, the paper explores XAI role in healthcare problems to clarify its necessity in safety-critical applications. The paper intends to establish a comprehensive understanding of XAI-related applications in the healthcare field by reviewing the related experimental results. To facilitate future research for filling research gaps, the importance of XAI models from different viewpoints and their limitations are investigated.

Homography augumented momentum constrastive learning for SAR image retrieval

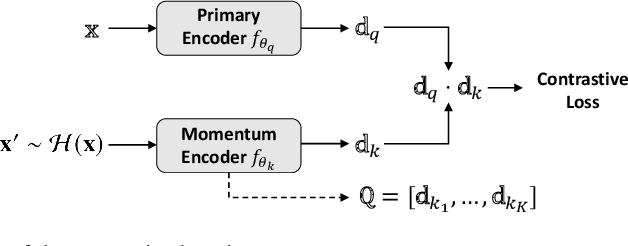
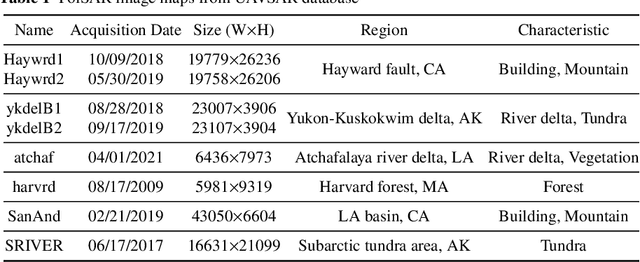
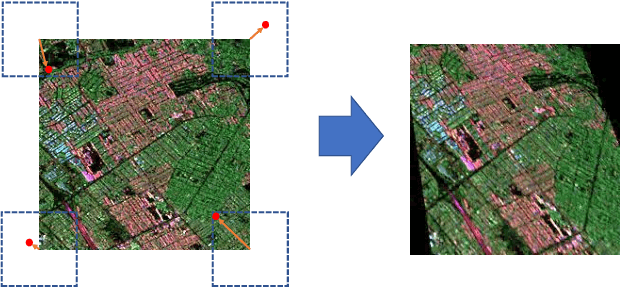
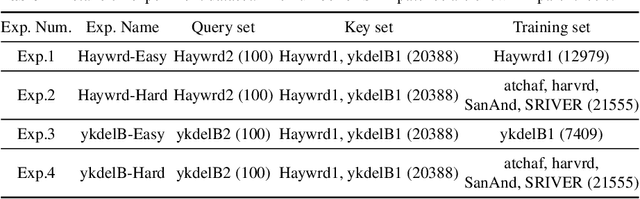
Deep learning-based image retrieval has been emphasized in computer vision. Representation embedding extracted by deep neural networks (DNNs) not only aims at containing semantic information of the image, but also can manage large-scale image retrieval tasks. In this work, we propose a deep learning-based image retrieval approach using homography transformation augmented contrastive learning to perform large-scale synthetic aperture radar (SAR) image search tasks. Moreover, we propose a training method for the DNNs induced by contrastive learning that does not require any labeling procedure. This may enable tractability of large-scale datasets with relative ease. Finally, we verify the performance of the proposed method by conducting experiments on the polarimetric SAR image datasets.

Deep Data Density Estimation through Donsker-Varadhan Representation

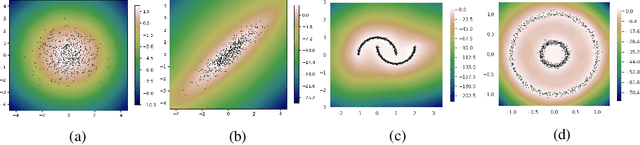
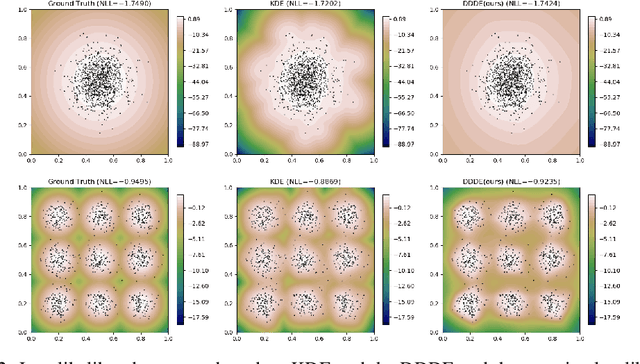
Estimating the data density is one of the challenging problems in deep learning. In this paper, we present a simple yet effective method for estimating the data density using a deep neural network and the Donsker-Varadhan variational lower bound on the KL divergence. We show that the optimal critic function associated with the Donsker-Varadhan representation on the KL divergence between the data and the uniform distribution can estimate the data density. We also present the deep neural network-based modeling and its stochastic learning. The experimental results and possible applications of the proposed method demonstrate that it is competitive with the previous methods and has a lot of possibilities in applied to various applications.

Interpreting Rate-Distortion of Variational Autoencoder and Using Model Uncertainty for Anomaly Detection

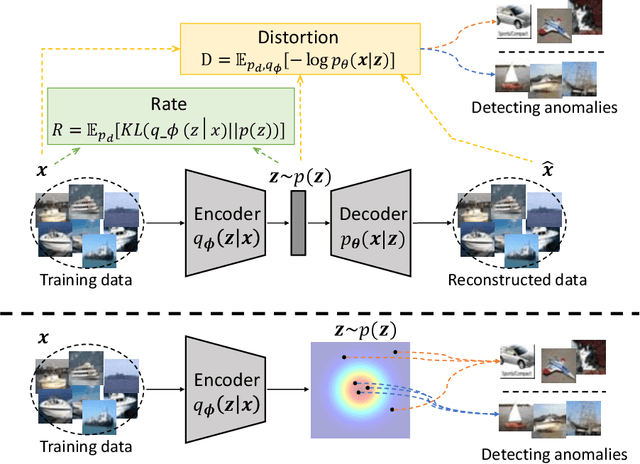
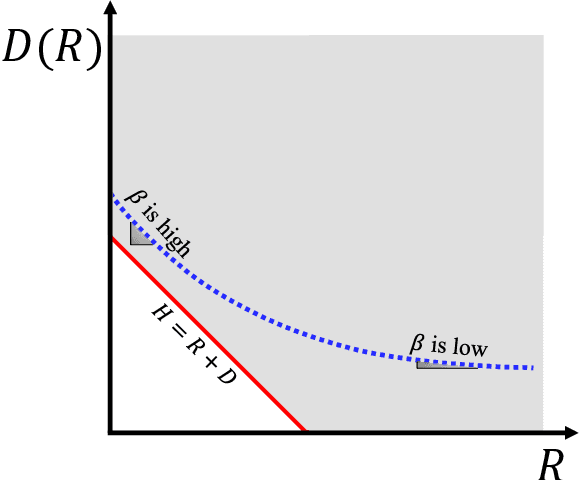
Building a scalable machine learning system for unsupervised anomaly detection via representation learning is highly desirable. One of the prevalent methods is using a reconstruction error from variational autoencoder (VAE) via maximizing the evidence lower bound. We revisit VAE from the perspective of information theory to provide some theoretical foundations on using the reconstruction error, and finally arrive at a simpler and more effective model for anomaly detection. In addition, to enhance the effectiveness of detecting anomalies, we incorporate a practical model uncertainty measure into the metric. We show empirically the competitive performance of our approach on benchmark datasets.

Combining Stochastic Adaptive Cubic Regularization with Negative Curvature for Nonconvex Optimization

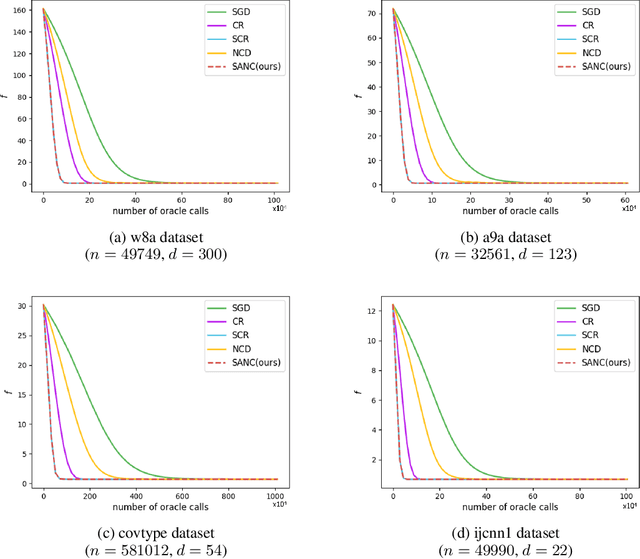
We focus on minimizing nonconvex finite-sum functions that typically arise in machine learning problems. In an attempt to solve this problem, the adaptive cubic regularized Newton method has shown its strong global convergence guarantees and ability to escape from strict saddle points. This method uses a trust region-like scheme to determine if an iteration is successful or not, and updates only when it is successful. In this paper, we suggest an algorithm combining negative curvature with the adaptive cubic regularized Newton method to update even at unsuccessful iterations. We call this new method Stochastic Adaptive cubic regularization with Negative Curvature (SANC). Unlike the previous method, in order to attain stochastic gradient and Hessian estimators, the SANC algorithm uses independent sets of data points of consistent size over all iterations. It makes the SANC algorithm more practical to apply for solving large-scale machine learning problems. To the best of our knowledge, this is the first approach that combines the negative curvature method with the adaptive cubic regularized Newton method. Finally, we provide experimental results including neural networks problems supporting the efficiency of our method.

Extended Vertical Lists for Temporal Pattern Mining from Multivariate Time Series

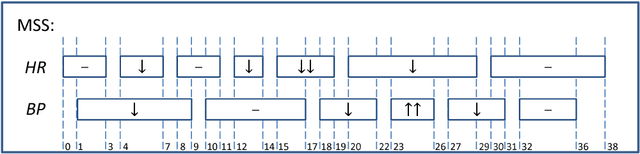
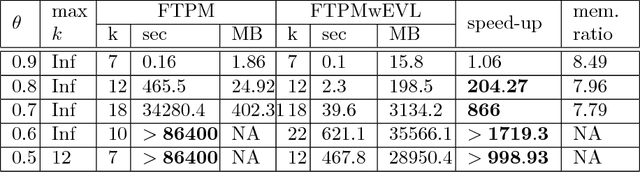
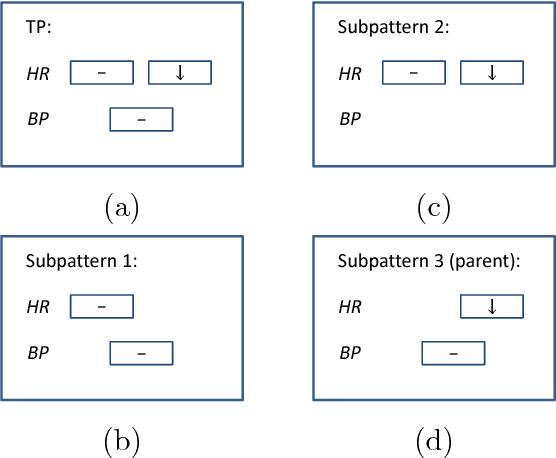
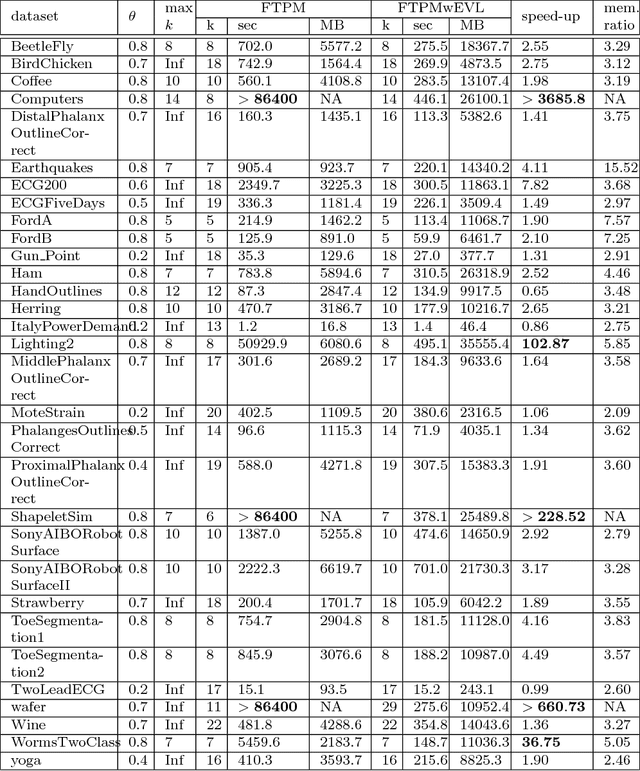
Temporal Pattern Mining (TPM) is the problem of mining predictive complex temporal patterns from multivariate time series in a supervised setting. We develop a new method called the Fast Temporal Pattern Mining with Extended Vertical Lists. This method utilizes an extension of the Apriori property which requires a more complex pattern to appear within records only at places where all of its subpatterns are detected as well. The approach is based on a novel data structure called the Extended Vertical List that tracks positions of the first state of the pattern inside records. Extensive computational results indicate that the new method performs significantly faster than the previous version of the algorithm for TMP. However, the speed-up comes at the expense of memory usage.

Machine Learning Methods for Solving Assignment Problems in Multi-Target Tracking

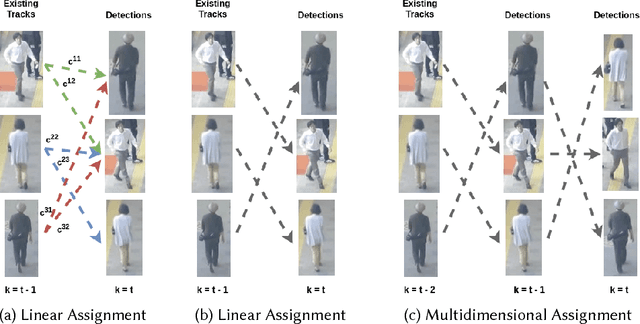
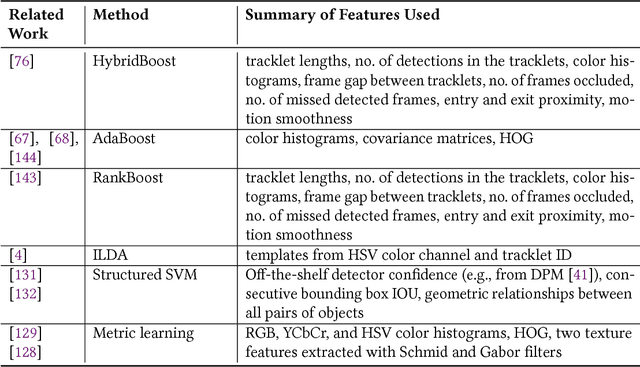
Data association and track-to-track association, two fundamental problems in single-sensor and multi-sensor multi-target tracking, are instances of an NP-hard combinatorial optimization problem known as the multidimensional assignment problem (MDAP). Over the last few years, data-driven approaches to tackling MDAPs in tracking have become increasingly popular. We argue that viewing multi-target tracking as an assignment problem conceptually unifies the wide variety of machine learning methods that have been proposed for data association and track-to-track association. In this survey, we review recent literature, provide rigorous formulations of the assignment problems encountered in multi-target tracking, and review classic approaches used prior to the shift towards data-driven techniques. Recent attempts at using deep learning to solve NP-hard combinatorial optimization problems, including data association, are discussed as well. We highlight representation learning methods for multi-sensor applications and conclude by providing an overview of current multi-target tracking benchmarks.

Optimal statistical decision for Gaussian graphical model selection

Gaussian graphical model is a graphical representation of the dependence structure for a Gaussian random vector. It is recognized as a powerful tool in different applied fields such as bioinformatics, error-control codes, speech language, information retrieval and others. Gaussian graphical model selection is a statistical problem to identify the Gaussian graphical model from a sample of a given size. Different approaches for Gaussian graphical model selection are suggested in the literature. One of them is based on considering the family of individual conditional independence tests. The application of this approach leads to the construction of a variety of multiple testing statistical procedures for Gaussian graphical model selection. An important characteristic of these procedures is its error rate for a given sample size. In existing literature great attention is paid to the control of error rates for incorrect edge inclusion (Type I error). However, in graphical model selection it is also important to take into account error rates for incorrect edge exclusion (Type II error). To deal with this issue we consider the graphical model selection problem in the framework of the multiple decision theory. The quality of statistical procedures is measured by a risk function with additive losses. Additive losses allow both types of errors to be taken into account. We construct the tests of a Neyman structure for individual hypotheses and combine them to obtain a multiple decision statistical procedure. We show that the obtained procedure is optimal in the sense that it minimizes the linear combination of expected numbers of Type I and Type II errors in the class of unbiased multiple decision procedures.