Regularized Q-Learning with Linear Function Approximation

Several successful reinforcement learning algorithms make use of regularization to promote multi-modal policies that exhibit enhanced exploration and robustness. With functional approximation, the convergence properties of some of these algorithms (e.g. soft Q-learning) are not well understood. In this paper, we consider a single-loop algorithm for minimizing the projected Bellman error with finite time convergence guarantees in the case of linear function approximation. The algorithm operates on two scales: a slower scale for updating the target network of the state-action values, and a faster scale for approximating the Bellman backups in the subspace of the span of basis vectors. We show that, under certain assumptions, the proposed algorithm converges to a stationary point in the presence of Markovian noise. In addition, we provide a performance guarantee for the policies derived from the proposed algorithm.

Extended Vertical Lists for Temporal Pattern Mining from Multivariate Time Series

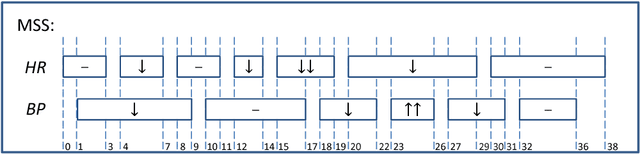
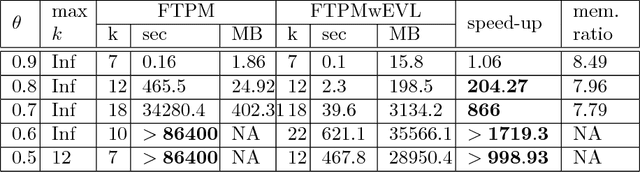
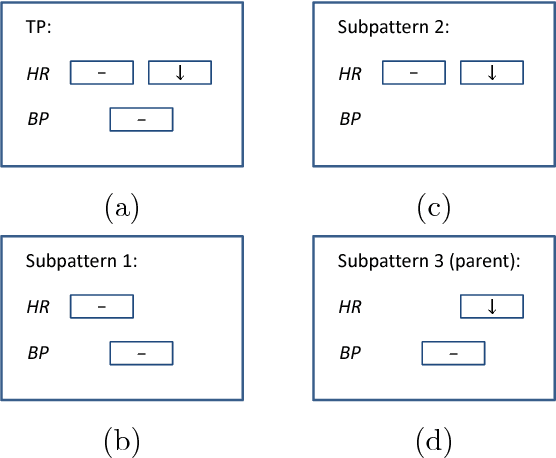
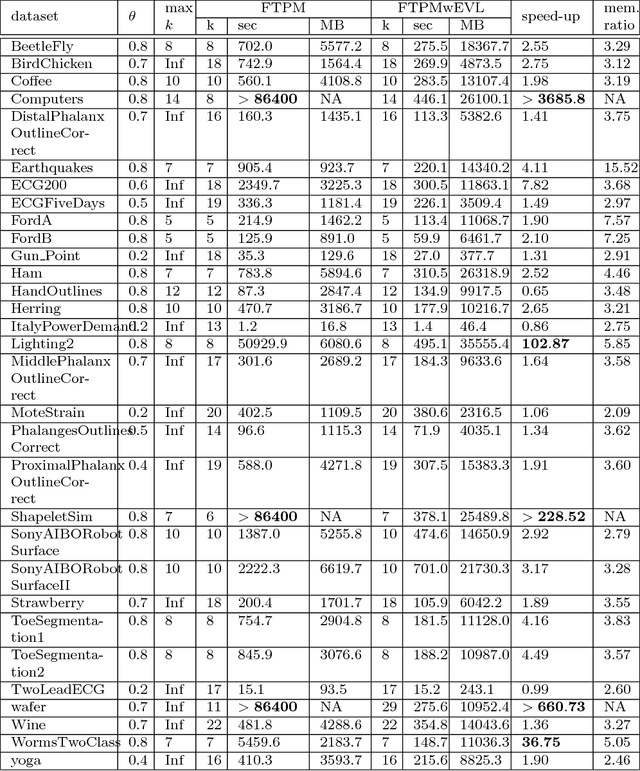
Temporal Pattern Mining (TPM) is the problem of mining predictive complex temporal patterns from multivariate time series in a supervised setting. We develop a new method called the Fast Temporal Pattern Mining with Extended Vertical Lists. This method utilizes an extension of the Apriori property which requires a more complex pattern to appear within records only at places where all of its subpatterns are detected as well. The approach is based on a novel data structure called the Extended Vertical List that tracks positions of the first state of the pattern inside records. Extensive computational results indicate that the new method performs significantly faster than the previous version of the algorithm for TMP. However, the speed-up comes at the expense of memory usage.