Deep Data Density Estimation through Donsker-Varadhan Representation
Paper and Code
Apr 14, 2021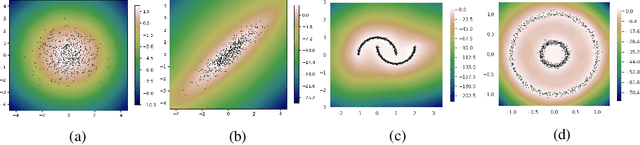

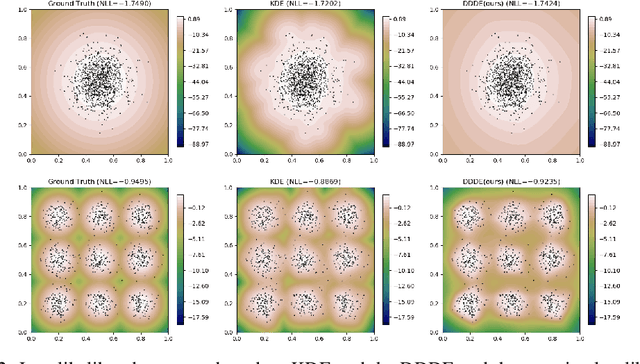

Estimating the data density is one of the challenging problems in deep learning. In this paper, we present a simple yet effective method for estimating the data density using a deep neural network and the Donsker-Varadhan variational lower bound on the KL divergence. We show that the optimal critic function associated with the Donsker-Varadhan representation on the KL divergence between the data and the uniform distribution can estimate the data density. We also present the deep neural network-based modeling and its stochastic learning. The experimental results and possible applications of the proposed method demonstrate that it is competitive with the previous methods and has a lot of possibilities in applied to various applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge