Learning Regionally Decentralized AC Optimal Power Flows with ADMM

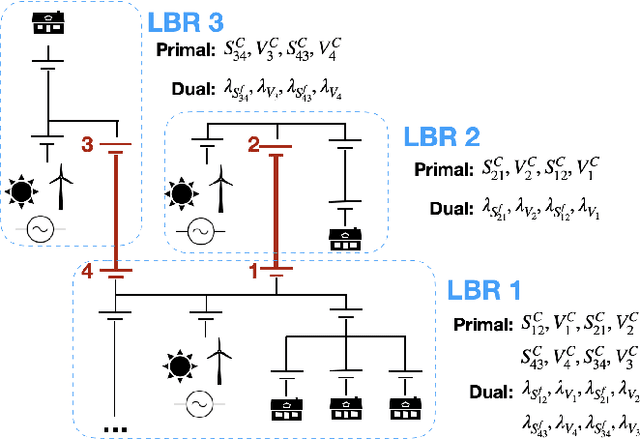
One potential future for the next generation of smart grids is the use of decentralized optimization algorithms and secured communications for coordinating renewable generation (e.g., wind/solar), dispatchable devices (e.g., coal/gas/nuclear generations), demand response, battery & storage facilities, and topology optimization. The Alternating Direction Method of Multipliers (ADMM) has been widely used in the community to address such decentralized optimization problems and, in particular, the AC Optimal Power Flow (AC-OPF). This paper studies how machine learning may help in speeding up the convergence of ADMM for solving AC-OPF. It proposes a novel decentralized machine-learning approach, namely ML-ADMM, where each agent uses deep learning to learn the consensus parameters on the coupling branches. The paper also explores the idea of learning only from ADMM runs that exhibit high-quality convergence properties, and proposes filtering mechanisms to select these runs. Experimental results on test cases based on the French system demonstrate the potential of the approach in speeding up the convergence of ADMM significantly.

Risk-Aware Control and Optimization for High-Renewable Power Grids

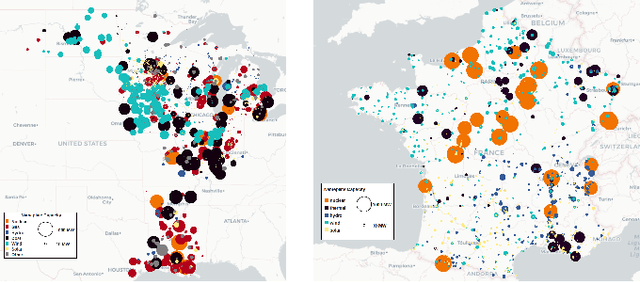
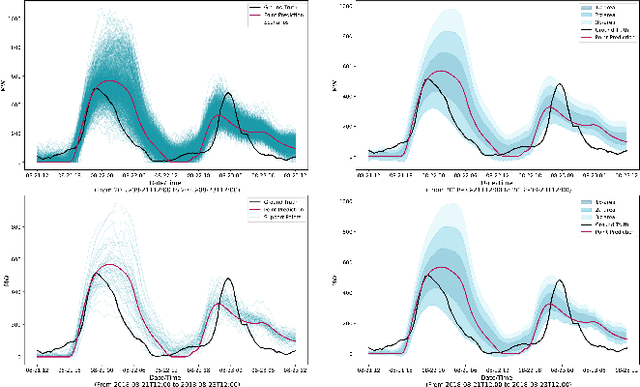
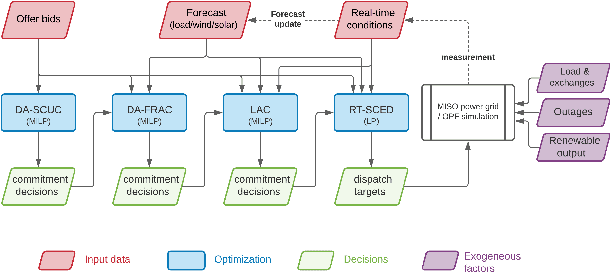
The transition of the electrical power grid from fossil fuels to renewable sources of energy raises fundamental challenges to the market-clearing algorithms that drive its operations. Indeed, the increased stochasticity in load and the volatility of renewable energy sources have led to significant increases in prediction errors, affecting the reliability and efficiency of existing deterministic optimization models. The RAMC project was initiated to investigate how to move from this deterministic setting into a risk-aware framework where uncertainty is quantified explicitly and incorporated in the market-clearing optimizations. Risk-aware market-clearing raises challenges on its own, primarily from a computational standpoint. This paper reviews how RAMC approaches risk-aware market clearing and presents some of its innovations in uncertainty quantification, optimization, and machine learning. Experimental results on real networks are presented.

Data-Driven Time Series Reconstruction for Modern Power Systems Research

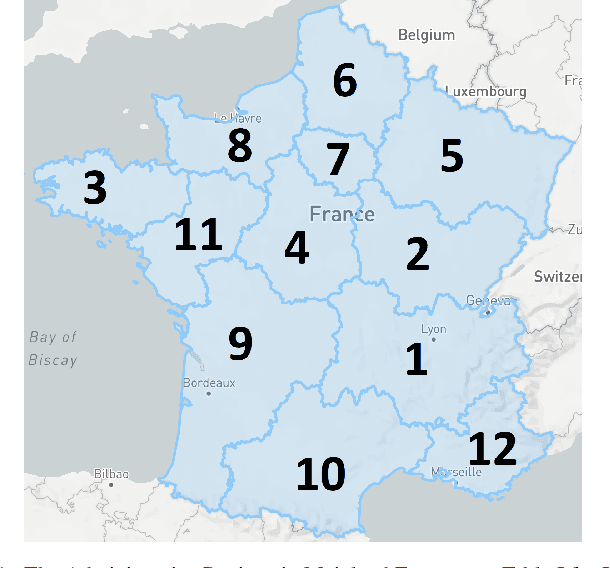
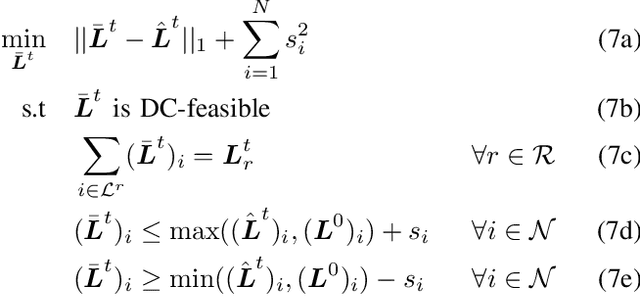
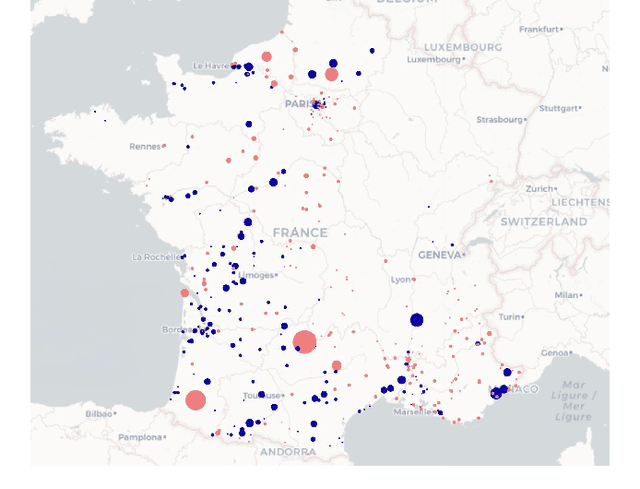
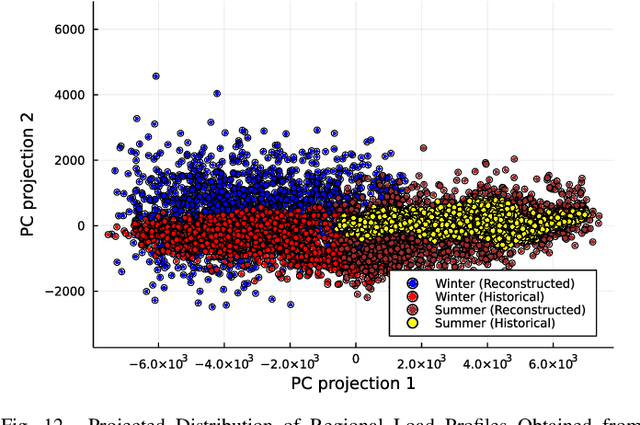
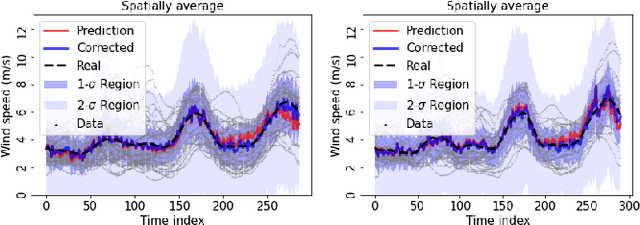
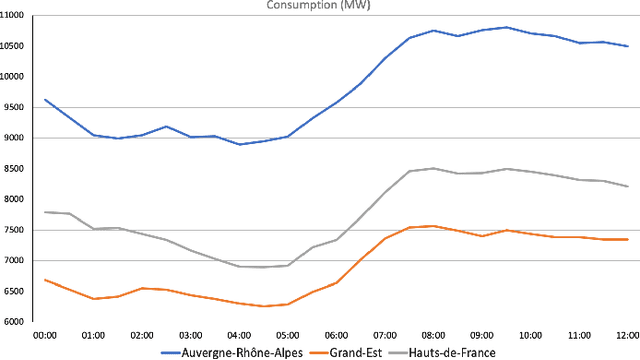
A critical aspect of power systems research is the availability of suitable data, access to which is limited by privacy concerns and the sensitive nature of energy infrastructure. This lack of data, in turn, hinders the development of modern research avenues such as machine learning approaches or stochastic formulations. To overcome this challenge, this paper proposes a systematic, data-driven framework for reconstructing high-fidelity time series, using publicly-available grid snapshots and historical data published by transmission system operators. The proposed approach, from geo-spatial data and generation capacity reconstruction, to time series disaggregation, is applied to the French transmission grid. Thereby, synthetic but highly realistic time series data, spanning multiple years with a 5-minute granularity, is generated at the individual component level.

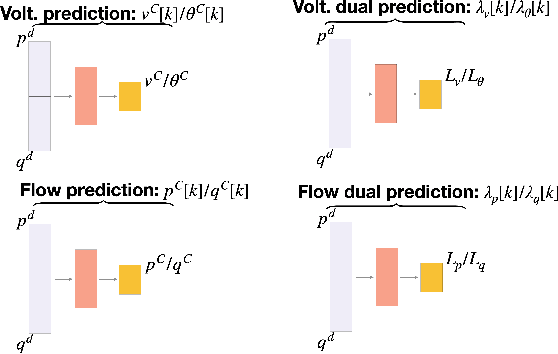
Spatial Network Decomposition for Fast and Scalable AC-OPF Learning

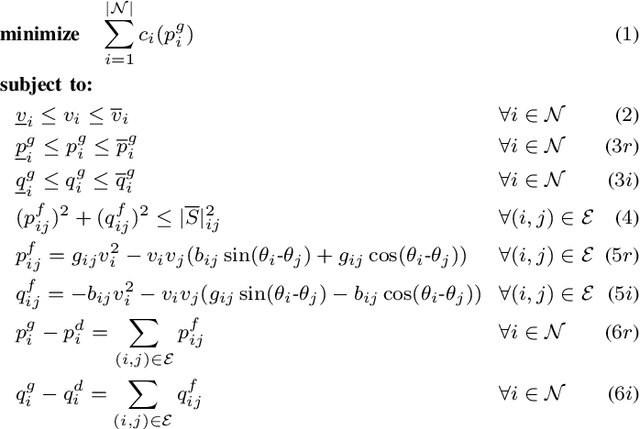
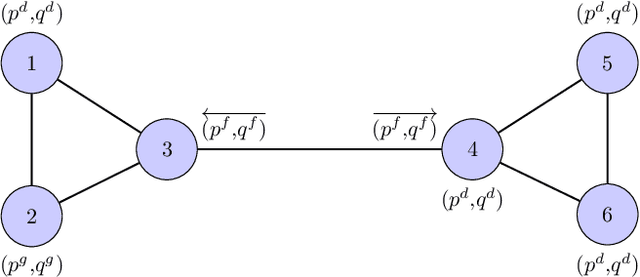
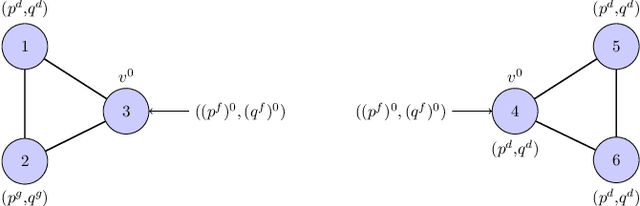
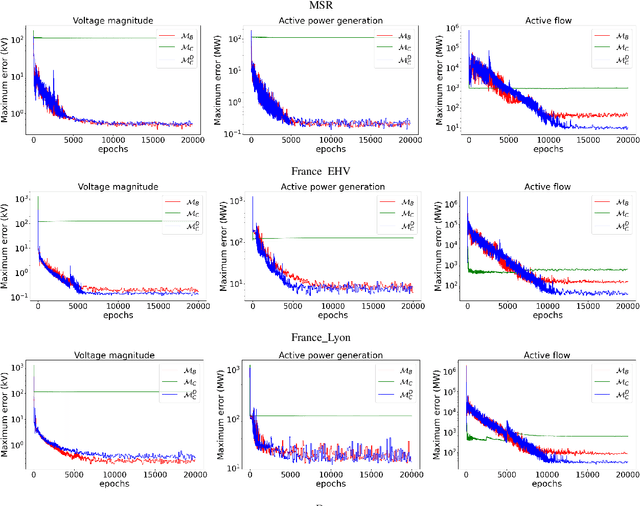
This paper proposes a novel machine-learning approach for predicting AC-OPF solutions that features a fast and scalable training. It is motivated by the two critical considerations: (1) the fact that topology optimization and the stochasticity induced by renewable energy sources may lead to fundamentally different AC-OPF instances; and (2) the significant training time needed by existing machine-learning approaches for predicting AC-OPF. The proposed approach is a 2-stage methodology that exploits a spatial decomposition of the power network that is viewed as a set of regions. The first stage learns to predict the flows and voltages on the buses and lines coupling the regions, and the second stage trains, in parallel, the machine-learning models for each region. Experimental results on the French transmission system (up to 6,700 buses and 9,000 lines) demonstrate the potential of the approach. Within a short training time, the approach predicts AC-OPF solutions with very high fidelity and minor constraint violations, producing significant improvements over the state-of-the-art. The results also show that the predictions can seed a load flow optimization to return a feasible solution within 0.03% of the AC-OPF objective, while reducing running times significantly.

High-Fidelity Machine Learning Approximations of Large-Scale Optimal Power Flow

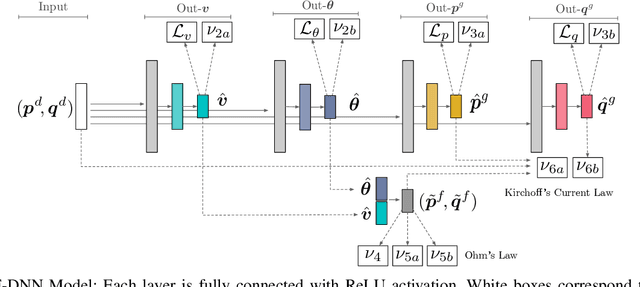
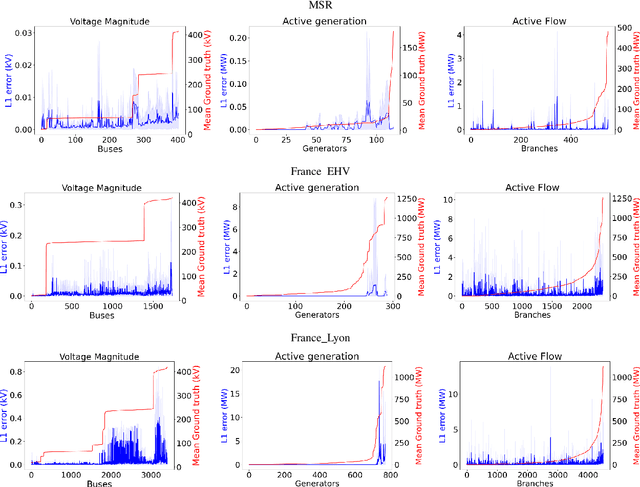
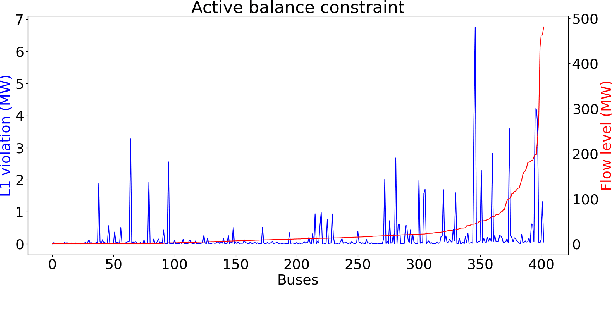
The AC Optimal Power Flow (AC-OPF) is a key building block in many power system applications. It determines generator setpoints at minimal cost that meet the power demands while satisfying the underlying physical and operational constraints. It is non-convex and NP-hard, and computationally challenging for large-scale power systems. Motivated by the increased stochasticity in generation schedules and increasing penetration of renewable sources, this paper explores a deep learning approach to deliver highly efficient and accurate approximations to the AC-OPF. In particular, the paper proposes an integration of deep neural networks and Lagrangian duality to capture the physical and operational constraints. The resulting model, called OPF-DNN, is evaluated on real case studies from the French transmission system, with up to 3,400 buses and 4,500 lines. Computational results show that OPF-DNN produces highly accurate AC-OPF approximations whose costs are within 0.01% of optimality. OPF-DNN generates, in milliseconds, solutions that capture the problem constraints with high fidelity.