Compact Optimization Learning for AC Optimal Power Flow

This paper reconsiders end-to-end learning approaches to the Optimal Power Flow (OPF). Existing methods, which learn the input/output mapping of the OPF, suffer from scalability issues due to the high dimensionality of the output space. This paper first shows that the space of optimal solutions can be significantly compressed using principal component analysis (PCA). It then proposes Compact Learning, a new method that learns in a subspace of the principal components before translating the vectors into the original output space. This compression reduces the number of trainable parameters substantially, improving scalability and effectiveness. Compact Learning is evaluated on a variety of test cases from the PGLib with up to 30,000 buses. The paper also shows that the output of Compact Learning can be used to warm-start an exact AC solver to restore feasibility, while bringing significant speed-ups.

Active Bucketized Learning for ACOPF Optimization Proxies

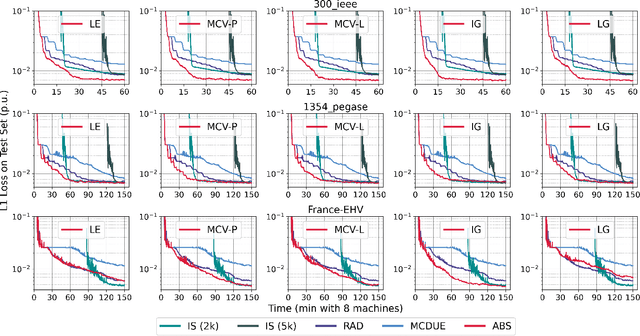
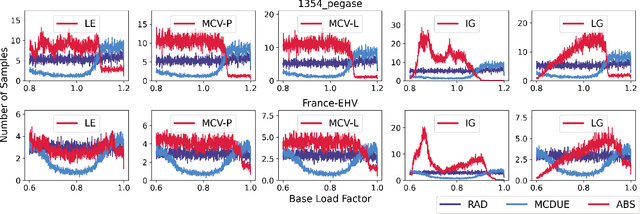
This paper considers optimization proxies for Optimal Power Flow (OPF), i.e., machine-learning models that approximate the input/output relationship of OPF. Recent work has focused on showing that such proxies can be of high fidelity. However, their training requires significant data, each instance necessitating the (offline) solving of an OPF for a sample of the input distribution. To meet the requirements of market-clearing applications, this paper proposes Active Bucketized Sampling (ABS), a novel active learning framework that aims at training the best possible OPF proxy within a time limit. ABS partitions the input distribution into buckets and uses an acquisition function to determine where to sample next. It relies on an adaptive learning rate that increases and decreases over time. Experimental results demonstrate the benefits of ABS.

Learning Regionally Decentralized AC Optimal Power Flows with ADMM

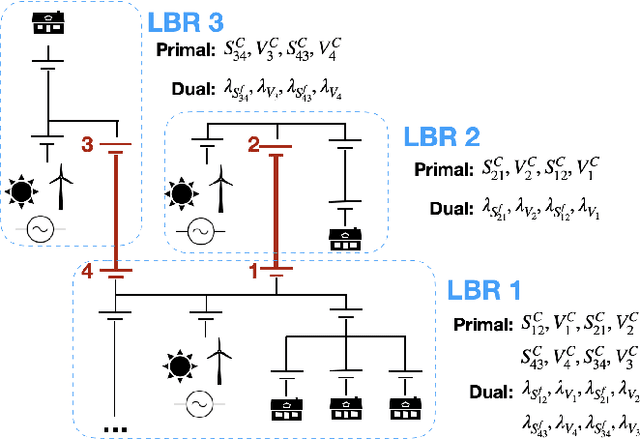
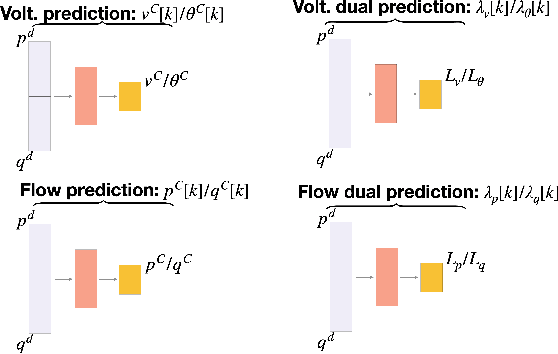
One potential future for the next generation of smart grids is the use of decentralized optimization algorithms and secured communications for coordinating renewable generation (e.g., wind/solar), dispatchable devices (e.g., coal/gas/nuclear generations), demand response, battery & storage facilities, and topology optimization. The Alternating Direction Method of Multipliers (ADMM) has been widely used in the community to address such decentralized optimization problems and, in particular, the AC Optimal Power Flow (AC-OPF). This paper studies how machine learning may help in speeding up the convergence of ADMM for solving AC-OPF. It proposes a novel decentralized machine-learning approach, namely ML-ADMM, where each agent uses deep learning to learn the consensus parameters on the coupling branches. The paper also explores the idea of learning only from ADMM runs that exhibit high-quality convergence properties, and proposes filtering mechanisms to select these runs. Experimental results on test cases based on the French system demonstrate the potential of the approach in speeding up the convergence of ADMM significantly.

Spatial Network Decomposition for Fast and Scalable AC-OPF Learning

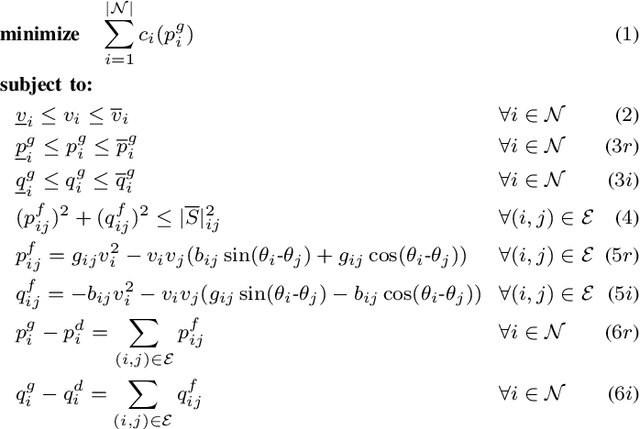
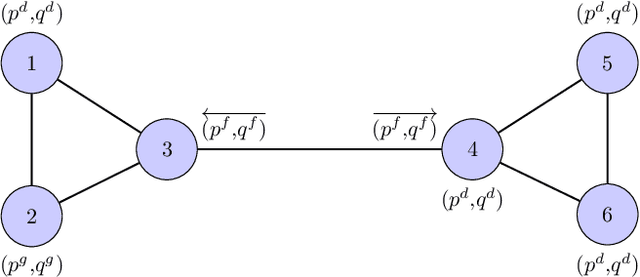
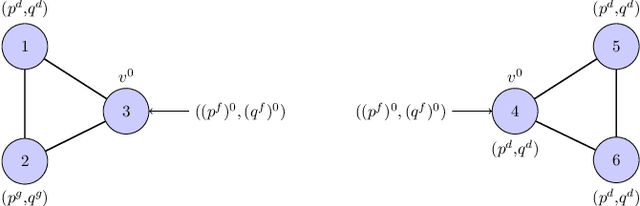
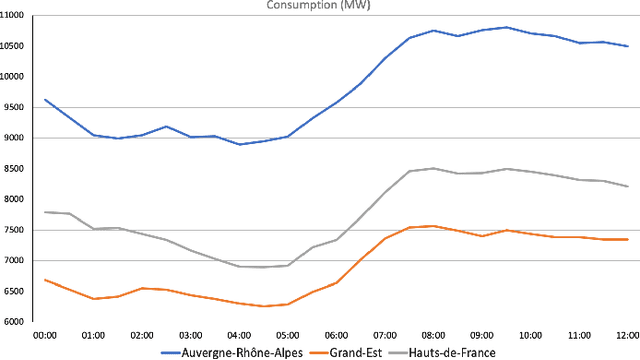
This paper proposes a novel machine-learning approach for predicting AC-OPF solutions that features a fast and scalable training. It is motivated by the two critical considerations: (1) the fact that topology optimization and the stochasticity induced by renewable energy sources may lead to fundamentally different AC-OPF instances; and (2) the significant training time needed by existing machine-learning approaches for predicting AC-OPF. The proposed approach is a 2-stage methodology that exploits a spatial decomposition of the power network that is viewed as a set of regions. The first stage learns to predict the flows and voltages on the buses and lines coupling the regions, and the second stage trains, in parallel, the machine-learning models for each region. Experimental results on the French transmission system (up to 6,700 buses and 9,000 lines) demonstrate the potential of the approach. Within a short training time, the approach predicts AC-OPF solutions with very high fidelity and minor constraint violations, producing significant improvements over the state-of-the-art. The results also show that the predictions can seed a load flow optimization to return a feasible solution within 0.03% of the AC-OPF objective, while reducing running times significantly.

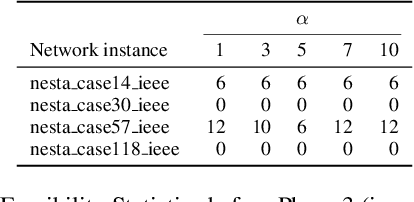
Load Embeddings for Scalable AC-OPF Learning

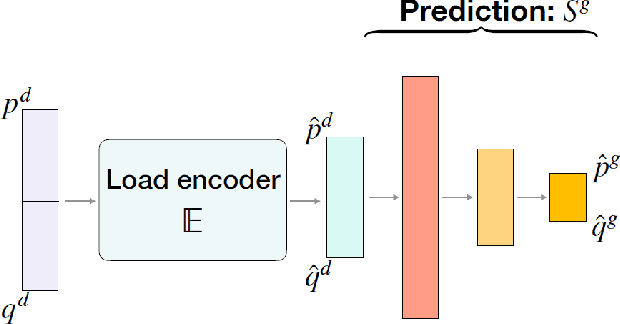
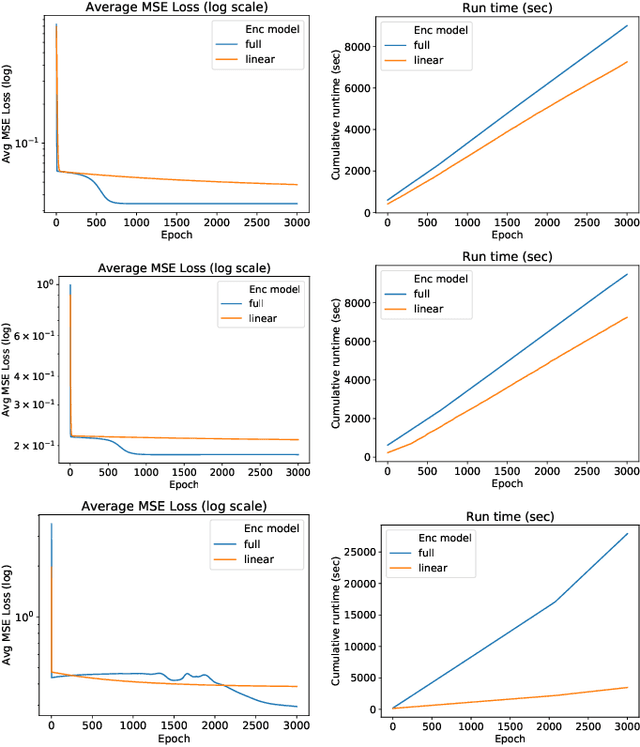
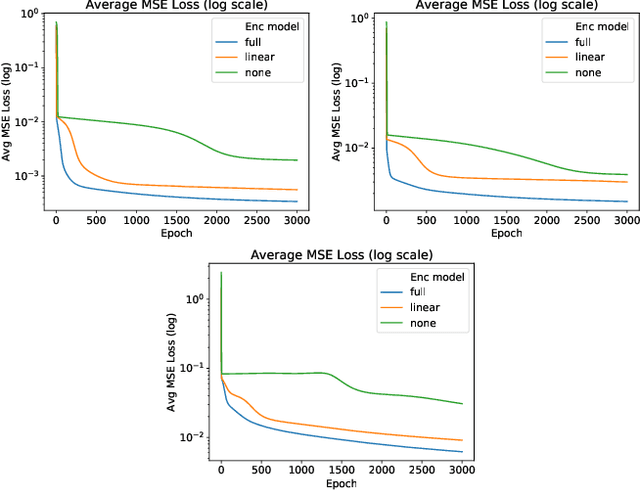
AC Optimal Power Flow (AC-OPF) is a fundamental building block in power system optimization. It is often solved repeatedly, especially in regions with large penetration of renewable generation, to avoid violating operational limits. Recent work has shown that deep learning can be effective in providing highly accurate approximations of AC-OPF. However, deep learning approaches may suffer from scalability issues, especially when applied to large realistic grids. This paper addresses these scalability limitations and proposes a load embedding scheme using a 3-step approach. The first step formulates the load embedding problem as a bilevel optimization model that can be solved using a penalty method. The second step learns the encoding optimization to quickly produce load embeddings for new OPF instances. The third step is a deep learning model that uses load embeddings to produce accurate AC-OPF approximations. The approach is evaluated experimentally on large-scale test cases from the NESTA library. The results demonstrate that the proposed approach produces an order of magnitude improvements in training convergence and prediction accuracy.

High-Fidelity Machine Learning Approximations of Large-Scale Optimal Power Flow

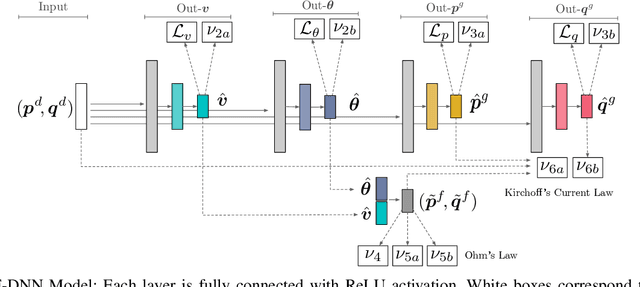
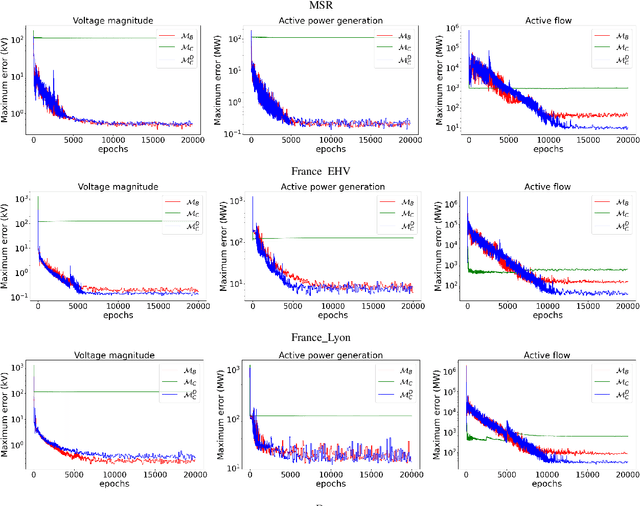
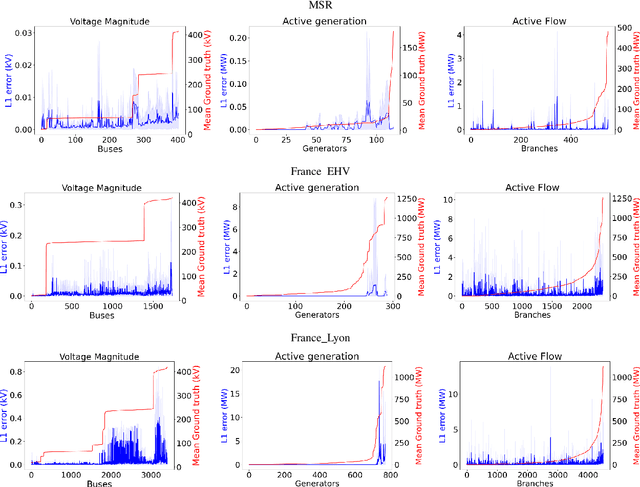
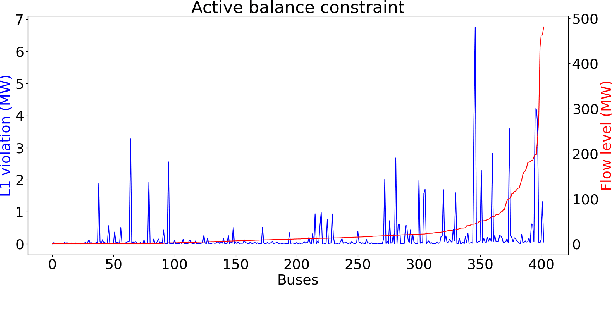
The AC Optimal Power Flow (AC-OPF) is a key building block in many power system applications. It determines generator setpoints at minimal cost that meet the power demands while satisfying the underlying physical and operational constraints. It is non-convex and NP-hard, and computationally challenging for large-scale power systems. Motivated by the increased stochasticity in generation schedules and increasing penetration of renewable sources, this paper explores a deep learning approach to deliver highly efficient and accurate approximations to the AC-OPF. In particular, the paper proposes an integration of deep neural networks and Lagrangian duality to capture the physical and operational constraints. The resulting model, called OPF-DNN, is evaluated on real case studies from the French transmission system, with up to 3,400 buses and 4,500 lines. Computational results show that OPF-DNN produces highly accurate AC-OPF approximations whose costs are within 0.01% of optimality. OPF-DNN generates, in milliseconds, solutions that capture the problem constraints with high fidelity.

Predicting AC Optimal Power Flows: Combining Deep Learning and Lagrangian Dual Methods

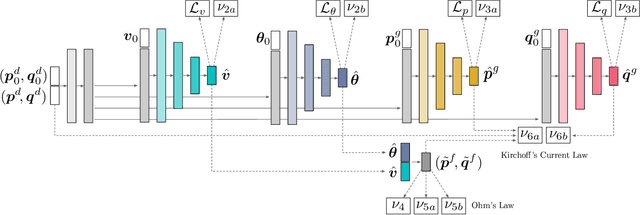
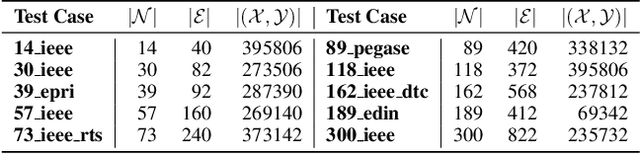
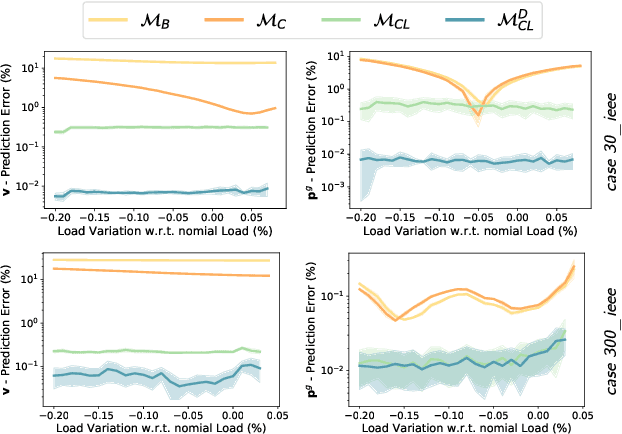
The Optimal Power Flow (OPF) problem is a fundamental building block for the optimization of electrical power systems. It is nonlinear and nonconvex and computes the generator setpoints for power and voltage, given a set of load demands. It is often needed to be solved repeatedly under various conditions, either in real-time or in large-scale studies. This need is further exacerbated by the increasing stochasticity of power systems due to renewable energy sources in front and behind the meter. To address these challenges, this paper presents a deep learning approach to the OPF. The learning model exploits the information available in the prior states of the system (which is commonly available in practical applications), as well as a dual Lagrangian method to satisfy the physical and engineering constraints present in the OPF. The proposed model is evaluated on a large collection of realistic power systems. The experimental results show that its predictions are highly accurate with average errors as low as 0.2%. Additionally, the proposed approach is shown to improve the accuracy of widely adopted OPF linear DC approximation by at least two orders of magnitude.

Privacy-Preserving Obfuscation of Critical Infrastructure Networks

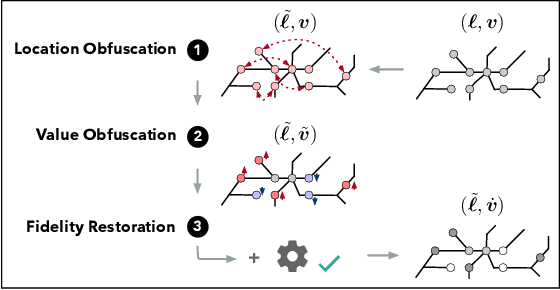
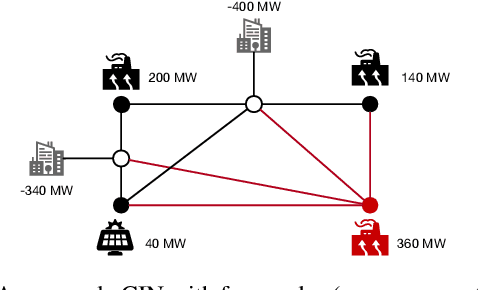
The paper studies how to release data about a critical infrastructure network (e.g., the power network or a transportation network) without disclosing sensitive information that can be exploited by malevolent agents, while preserving the realism of the network. It proposes a novel obfuscation mechanism that combines several privacy-preserving building blocks with a bi-level optimization model to significantly improve accuracy. The obfuscation is evaluated for both realism and privacy properties on real energy and transportation networks. Experimental results show the obfuscation mechanism substantially reduces the potential damage of an attack exploiting the released data to harm the real network.

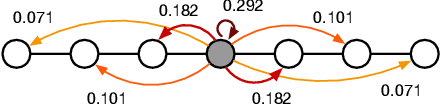
Differential Privacy for Power Grid Obfuscation

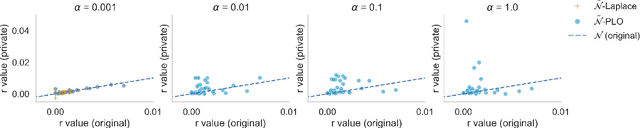
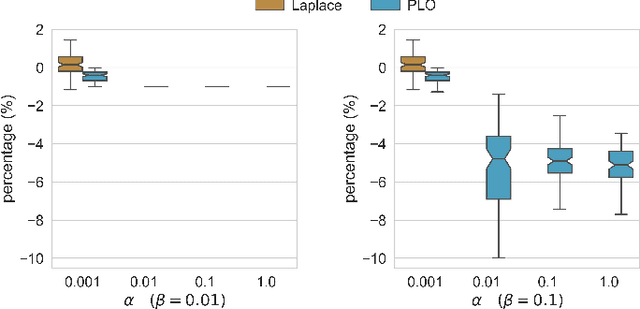
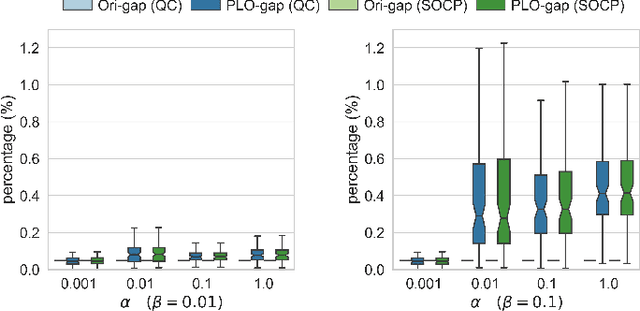
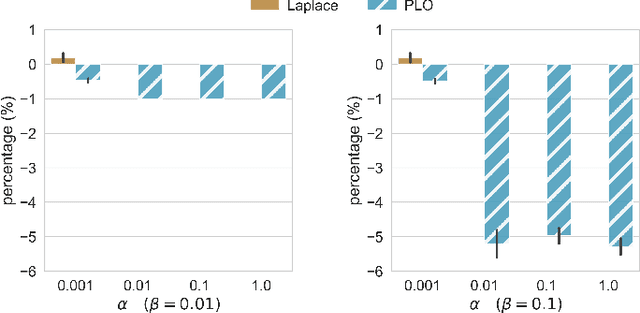
The availability of high-fidelity energy networks brings significant value to academic and commercial research. However, such releases also raise fundamental concerns related to privacy and security as they can reveal sensitive commercial information and expose system vulnerabilities. This paper investigates how to release power networks where the parameters of transmission lines and transformers are obfuscated. It does so by using the framework of Differential Privacy (DP), that provides strong privacy guarantees and has attracted significant attention in recent years. Unfortunately, simple DP mechanisms often result in AC-infeasible networks. To address these concerns, this paper presents a novel differential privacy mechanism that guarantees AC-feasibility and largely preserves the fidelity of the obfuscated network. Experimental results also show that the obfuscation significantly reduces the potential damage of an attacker exploiting the release of the dataset.