Predicting AC Optimal Power Flows: Combining Deep Learning and Lagrangian Dual Methods
Paper and Code
Sep 19, 2019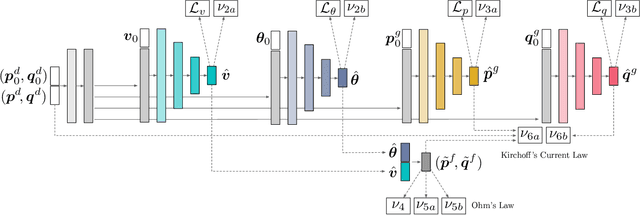
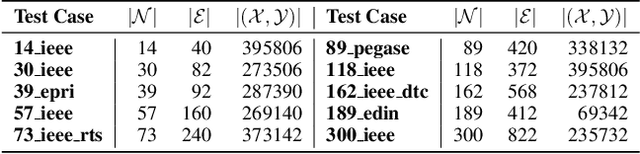
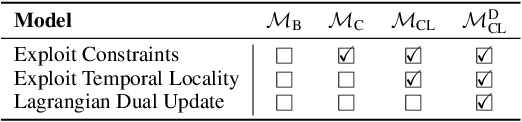
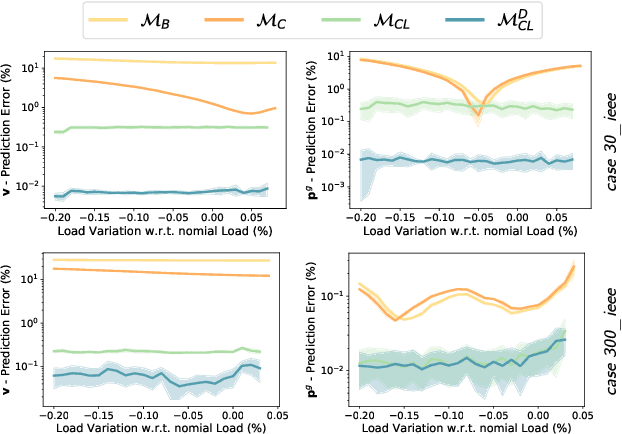
The Optimal Power Flow (OPF) problem is a fundamental building block for the optimization of electrical power systems. It is nonlinear and nonconvex and computes the generator setpoints for power and voltage, given a set of load demands. It is often needed to be solved repeatedly under various conditions, either in real-time or in large-scale studies. This need is further exacerbated by the increasing stochasticity of power systems due to renewable energy sources in front and behind the meter. To address these challenges, this paper presents a deep learning approach to the OPF. The learning model exploits the information available in the prior states of the system (which is commonly available in practical applications), as well as a dual Lagrangian method to satisfy the physical and engineering constraints present in the OPF. The proposed model is evaluated on a large collection of realistic power systems. The experimental results show that its predictions are highly accurate with average errors as low as 0.2%. Additionally, the proposed approach is shown to improve the accuracy of widely adopted OPF linear DC approximation by at least two orders of magnitude.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge