AutoSchA: Automatic Hierarchical Music Representations via Multi-Relational Node Isolation

Hierarchical representations provide powerful and principled approaches for analyzing many musical genres. Such representations have been broadly studied in music theory, for instance via Schenkerian analysis (SchA). Hierarchical music analyses, however, are highly cost-intensive; the analysis of a single piece of music requires a great deal of time and effort from trained experts. The representation of hierarchical analyses in a computer-readable format is a further challenge. Given recent developments in hierarchical deep learning and increasing quantities of computer-readable data, there is great promise in extending such work for an automatic hierarchical representation framework. This paper thus introduces a novel approach, AutoSchA, which extends recent developments in graph neural networks (GNNs) for hierarchical music analysis. AutoSchA features three key contributions: 1) a new graph learning framework for hierarchical music representation, 2) a new graph pooling mechanism based on node isolation that directly optimizes learned pooling assignments, and 3) a state-of-the-art architecture that integrates such developments for automatic hierarchical music analysis. We show, in a suite of experiments, that AutoSchA performs comparably to human experts when analyzing Baroque fugue subjects.

QuIP: Experimental design for expensive simulators with many Qualitative factors via Integer Programming

The need to explore and/or optimize expensive simulators with many qualitative factors arises in broad scientific and engineering problems. Our motivating application lies in path planning - the exploration of feasible paths for navigation, which plays an important role in robotics, surgical planning and assembly planning. Here, the feasibility of a path is evaluated via expensive virtual experiments, and its parameter space is typically discrete and high-dimensional. A carefully selected experimental design is thus essential for timely decision-making. We propose here a novel framework, called QuIP, for experimental design of Qualitative factors via Integer Programming under a Gaussian process surrogate model with an exchangeable covariance function. For initial design, we show that its asymptotic D-optimal design can be formulated as a variant of the well-known assignment problem in operations research, which can be efficiently solved to global optimality using state-of-the-art integer programming solvers. For sequential design (specifically, for active learning or black-box optimization), we show that its design criterion can similarly be formulated as an assignment problem, thus enabling efficient and reliable optimization with existing solvers. We then demonstrate the effectiveness of QuIP over existing methods in a suite of path planning experiments and an application to rover trajectory optimization.

Local transfer learning Gaussian process modeling, with applications to surrogate modeling of expensive computer simulators

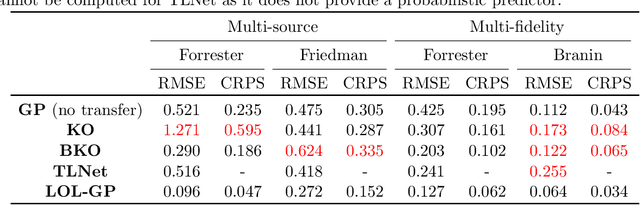
A critical bottleneck for scientific progress is the costly nature of computer simulations for complex systems. Surrogate models provide an appealing solution: such models are trained on simulator evaluations, then used to emulate and quantify uncertainty on the expensive simulator at unexplored inputs. In many applications, one often has available data on related systems. For example, in designing a new jet turbine, there may be existing studies on turbines with similar configurations. A key question is how information from such "source" systems can be transferred for effective surrogate training on the "target" system of interest. We thus propose a new LOcal transfer Learning Gaussian Process (LOL-GP) model, which leverages a carefully-designed Gaussian process to transfer such information for surrogate modeling. The key novelty of the LOL-GP is a latent regularization model, which identifies regions where transfer should be performed and regions where it should be avoided. This "local transfer" property is desirable in scientific systems: at certain parameters, such systems may behave similarly and thus transfer is beneficial; at other parameters, they may behave differently and thus transfer is detrimental. By accounting for local transfer, the LOL-GP can rectify a critical limitation of "negative transfer" in existing transfer learning models, where the transfer of information worsens predictive performance. We derive a Gibbs sampling algorithm for efficient posterior predictive sampling on the LOL-GP, for both the multi-source and multi-fidelity transfer settings. We then show, via a suite of numerical experiments and an application for jet turbine design, the improved surrogate performance of the LOL-GP over existing methods.

Diverse Expected Improvement (DEI): Diverse Bayesian Optimization of Expensive Computer Simulators

The optimization of expensive black-box simulators arises in a myriad of modern scientific and engineering applications. Bayesian optimization provides an appealing solution, by leveraging a fitted surrogate model to guide the selection of subsequent simulator evaluations. In practice, however, the objective is often not to obtain a single good solution, but rather a ''basket'' of good solutions from which users can choose for downstream decision-making. This need arises in our motivating application for real-time control of internal combustion engines for flight propulsion, where a diverse set of control strategies is essential for stable flight control. There has been little work on this front for Bayesian optimization. We thus propose a new Diverse Expected Improvement (DEI) method that searches for diverse ''$\epsilon$-optimal'' solutions: locally-optimal solutions within a tolerance level $\epsilon > 0$ from a global optimum. We show that DEI yields a closed-form acquisition function under a Gaussian process surrogate model, which facilitates efficient sequential queries via automatic differentiation. This closed form further reveals a novel exploration-exploitation-diversity trade-off, which incorporates the desired diversity property within the well-known exploration-exploitation trade-off. We demonstrate the improvement of DEI over existing methods in a suite of numerical experiments, then explore the DEI in two applications on rover trajectory optimization and engine control for flight propulsion.

A New Dataset, Notation Software, and Representation for Computational Schenkerian Analysis

Schenkerian Analysis (SchA) is a uniquely expressive method of music analysis, combining elements of melody, harmony, counterpoint, and form to describe the hierarchical structure supporting a work of music. However, despite its powerful analytical utility and potential to improve music understanding and generation, SchA has rarely been utilized by the computer music community. This is in large part due to the paucity of available high-quality data in a computer-readable format. With a larger corpus of Schenkerian data, it may be possible to infuse machine learning models with a deeper understanding of musical structure, thus leading to more "human" results. To encourage further research in Schenkerian analysis and its potential benefits for music informatics and generation, this paper presents three main contributions: 1) a new and growing dataset of SchAs, the largest in human- and computer-readable formats to date (>140 excerpts), 2) a novel software for visualization and collection of SchA data, and 3) a novel, flexible representation of SchA as a heterogeneous-edge graph data structure.

Targeted Variance Reduction: Robust Bayesian Optimization of Black-Box Simulators with Noise Parameters

The optimization of a black-box simulator over control parameters $\mathbf{x}$ arises in a myriad of scientific applications. In such applications, the simulator often takes the form $f(\mathbf{x},\boldsymbol{\theta})$, where $\boldsymbol{\theta}$ are parameters that are uncertain in practice. Robust optimization aims to optimize the objective $\mathbb{E}[f(\mathbf{x},\boldsymbol{\Theta})]$, where $\boldsymbol{\Theta} \sim \mathcal{P}$ is a random variable that models uncertainty on $\boldsymbol{\theta}$. For this, existing black-box methods typically employ a two-stage approach for selecting the next point $(\mathbf{x},\boldsymbol{\theta})$, where $\mathbf{x}$ and $\boldsymbol{\theta}$ are optimized separately via different acquisition functions. As such, these approaches do not employ a joint acquisition over $(\mathbf{x},\boldsymbol{\theta})$, and thus may fail to fully exploit control-to-noise interactions for effective robust optimization. To address this, we propose a new Bayesian optimization method called Targeted Variance Reduction (TVR). The TVR leverages a novel joint acquisition function over $(\mathbf{x},\boldsymbol{\theta})$, which targets variance reduction on the objective within the desired region of improvement. Under a Gaussian process surrogate on $f$, the TVR acquisition can be evaluated in closed form, and reveals an insightful exploration-exploitation-precision trade-off for robust black-box optimization. The TVR can further accommodate a broad class of non-Gaussian distributions on $\mathcal{P}$ via a careful integration of normalizing flows. We demonstrate the improved performance of TVR over the state-of-the-art in a suite of numerical experiments and an application to the robust design of automobile brake discs under operational uncertainty.

$e^{\text{RPCA}}$: Robust Principal Component Analysis for Exponential Family Distributions

Robust Principal Component Analysis (RPCA) is a widely used method for recovering low-rank structure from data matrices corrupted by significant and sparse outliers. These corruptions may arise from occlusions, malicious tampering, or other causes for anomalies, and the joint identification of such corruptions with low-rank background is critical for process monitoring and diagnosis. However, existing RPCA methods and their extensions largely do not account for the underlying probabilistic distribution for the data matrices, which in many applications are known and can be highly non-Gaussian. We thus propose a new method called Robust Principal Component Analysis for Exponential Family distributions ($e^{\text{RPCA}}$), which can perform the desired decomposition into low-rank and sparse matrices when such a distribution falls within the exponential family. We present a novel alternating direction method of multiplier optimization algorithm for efficient $e^{\text{RPCA}}$ decomposition. The effectiveness of $e^{\text{RPCA}}$ is then demonstrated in two applications: the first for steel sheet defect detection, and the second for crime activity monitoring in the Atlanta metropolitan area.

Trigonometric Quadrature Fourier Features for Scalable Gaussian Process Regression

Fourier feature approximations have been successfully applied in the literature for scalable Gaussian Process (GP) regression. In particular, Quadrature Fourier Features (QFF) derived from Gaussian quadrature rules have gained popularity in recent years due to their improved approximation accuracy and better calibrated uncertainty estimates compared to Random Fourier Feature (RFF) methods. However, a key limitation of QFF is that its performance can suffer from well-known pathologies related to highly oscillatory quadrature, resulting in mediocre approximation with limited features. We address this critical issue via a new Trigonometric Quadrature Fourier Feature (TQFF) method, which uses a novel non-Gaussian quadrature rule specifically tailored for the desired Fourier transform. We derive an exact quadrature rule for TQFF, along with kernel approximation error bounds for the resulting feature map. We then demonstrate the improved performance of our method over RFF and Gaussian QFF in a suite of numerical experiments and applications, and show the TQFF enjoys accurate GP approximations over a broad range of length-scales using fewer features.

Additive Multi-Index Gaussian process modeling, with application to multi-physics surrogate modeling of the quark-gluon plasma

The Quark-Gluon Plasma (QGP) is a unique phase of nuclear matter, theorized to have filled the Universe shortly after the Big Bang. A critical challenge in studying the QGP is that, to reconcile experimental observables with theoretical parameters, one requires many simulation runs of a complex physics model over a high-dimensional parameter space. Each run is computationally very expensive, requiring thousands of CPU hours, thus limiting physicists to only several hundred runs. Given limited training data for high-dimensional prediction, existing surrogate models often yield poor predictions with high predictive uncertainties, leading to imprecise scientific findings. To address this, we propose a new Additive Multi-Index Gaussian process (AdMIn-GP) model, which leverages a flexible additive structure on low-dimensional embeddings of the parameter space. This is guided by prior scientific knowledge that the QGP is dominated by multiple distinct physical phenomena (i.e., multiphysics), each involving a small number of latent parameters. The AdMIn-GP models for such embedded structures within a flexible Bayesian nonparametric framework, which facilitates efficient model fitting via a carefully constructed variational inference approach with inducing points. We show the effectiveness of the AdMIn-GP via a suite of numerical experiments and our QGP application, where we demonstrate considerably improved surrogate modeling performance over existing models.

Hierarchical shrinkage Gaussian processes: applications to computer code emulation and dynamical system recovery

In many areas of science and engineering, computer simulations are widely used as proxies for physical experiments, which can be infeasible or unethical. Such simulations can often be computationally expensive, and an emulator can be trained to efficiently predict the desired response surface. A widely-used emulator is the Gaussian process (GP), which provides a flexible framework for efficient prediction and uncertainty quantification. Standard GPs, however, do not capture structured sparsity on the underlying response surface, which is present in many applications, particularly in the physical sciences. We thus propose a new hierarchical shrinkage GP (HierGP), which incorporates such structure via cumulative shrinkage priors within a GP framework. We show that the HierGP implicitly embeds the well-known principles of effect sparsity, heredity and hierarchy for analysis of experiments, which allows our model to identify structured sparse features from the response surface with limited data. We propose efficient posterior sampling algorithms for model training and prediction, and prove desirable consistency properties for the HierGP. Finally, we demonstrate the improved performance of HierGP over existing models, in a suite of numerical experiments and an application to dynamical system recovery.