Resolving Predictive Multiplicity for the Rashomon Set

The existence of multiple, equally accurate models for a given predictive task leads to predictive multiplicity, where a ``Rashomon set'' of models achieve similar accuracy but diverges in their individual predictions. This inconsistency undermines trust in high-stakes applications where we want consistent predictions. We propose three approaches to reduce inconsistency among predictions for the members of the Rashomon set. The first approach is \textbf{outlier correction}. An outlier has a label that none of the good models are capable of predicting correctly. Outliers can cause the Rashomon set to have high variance predictions in a local area, so fixing them can lower variance. Our second approach is local patching. In a local region around a test point, models may disagree with each other because some of them are biased. We can detect and fix such biases using a validation set, which also reduces multiplicity. Our third approach is pairwise reconciliation, where we find pairs of models that disagree on a region around the test point. We modify predictions that disagree, making them less biased. These three approaches can be used together or separately, and they each have distinct advantages. The reconciled predictions can then be distilled into a single interpretable model for real-world deployment. In experiments across multiple datasets, our methods reduce disagreement metrics while maintaining competitive accuracy.

AutoSchA: Automatic Hierarchical Music Representations via Multi-Relational Node Isolation

Hierarchical representations provide powerful and principled approaches for analyzing many musical genres. Such representations have been broadly studied in music theory, for instance via Schenkerian analysis (SchA). Hierarchical music analyses, however, are highly cost-intensive; the analysis of a single piece of music requires a great deal of time and effort from trained experts. The representation of hierarchical analyses in a computer-readable format is a further challenge. Given recent developments in hierarchical deep learning and increasing quantities of computer-readable data, there is great promise in extending such work for an automatic hierarchical representation framework. This paper thus introduces a novel approach, AutoSchA, which extends recent developments in graph neural networks (GNNs) for hierarchical music analysis. AutoSchA features three key contributions: 1) a new graph learning framework for hierarchical music representation, 2) a new graph pooling mechanism based on node isolation that directly optimizes learned pooling assignments, and 3) a state-of-the-art architecture that integrates such developments for automatic hierarchical music analysis. We show, in a suite of experiments, that AutoSchA performs comparably to human experts when analyzing Baroque fugue subjects.

NodMAISI: Nodule-Oriented Medical AI for Synthetic Imaging

Objective: Although medical imaging datasets are increasingly available, abnormal and annotation-intensive findings critical to lung cancer screening, particularly small pulmonary nodules, remain underrepresented and inconsistently curated. Methods: We introduce NodMAISI, an anatomically constrained, nodule-oriented CT synthesis and augmentation framework trained on a unified multi-source cohort (7,042 patients, 8,841 CTs, 14,444 nodules). The framework integrates: (i) a standardized curation and annotation pipeline linking each CT with organ masks and nodule-level annotations, (ii) a ControlNet-conditioned rectified-flow generator built on MAISI-v2's foundational blocks to enforce anatomy- and lesion-consistent synthesis, and (iii) lesion-aware augmentation that perturbs nodule masks (controlled shrinkage) while preserving surrounding anatomy to generate paired CT variants. Results: Across six public test datasets, NodMAISI improved distributional fidelity relative to MAISI-v2 (real-to-synthetic FID range 1.18 to 2.99 vs 1.69 to 5.21). In lesion detectability analysis using a MONAI nodule detector, NodMAISI substantially increased average sensitivity and more closely matched clinical scans (IMD-CT: 0.69 vs 0.39; DLCS24: 0.63 vs 0.20), with the largest gains for sub-centimeter nodules where MAISI-v2 frequently failed to reproduce the conditioned lesion. In downstream nodule-level malignancy classification trained on LUNA25 and externally evaluated on LUNA16, LNDbv4, and DLCS24, NodMAISI augmentation improved AUC by 0.07 to 0.11 at <=20% clinical data and by 0.12 to 0.21 at 10%, consistently narrowing the performance gap under data scarcity.

It's LIT! Reliability-Optimized LLMs with Inspectable Tools

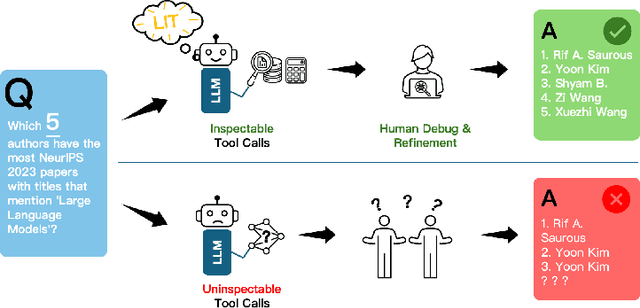
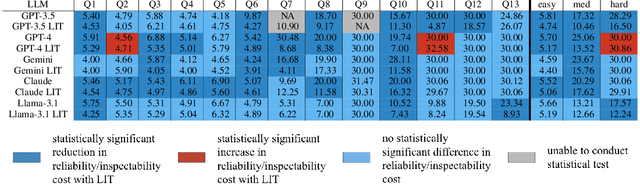
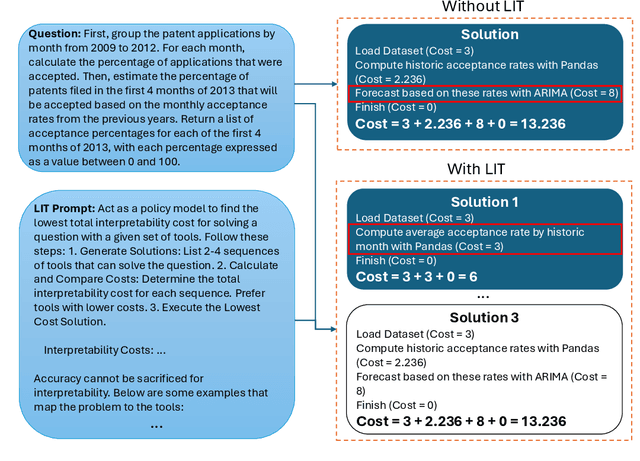
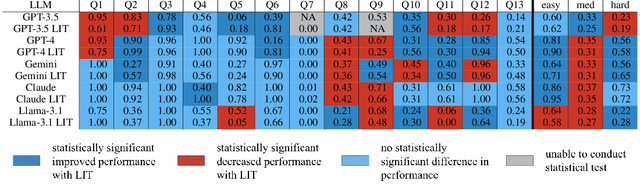
Large language models (LLMs) have exhibited remarkable capabilities across various domains. The ability to call external tools further expands their capability to handle real-world tasks. However, LLMs often follow an opaque reasoning process, which limits their usefulness in high-stakes domains where solutions need to be trustworthy to end users. LLMs can choose solutions that are unreliable and difficult to troubleshoot, even if better options are available. We address this issue by forcing LLMs to use external -- more reliable -- tools to solve problems when possible. We present a framework built on the tool-calling capabilities of existing LLMs to enable them to select the most reliable and easy-to-troubleshoot solution path, which may involve multiple sequential tool calls. We refer to this framework as LIT (LLMs with Inspectable Tools). In order to support LIT, we introduce a new and challenging benchmark dataset of 1,300 questions and a customizable set of reliability cost functions associated with a collection of specialized tools. These cost functions summarize how reliable each tool is and how easy it is to troubleshoot. For instance, a calculator is reliable across domains, whereas a linear prediction model is not reliable if there is distribution shift, but it is easy to troubleshoot. A tool that constructs a random forest is neither reliable nor easy to troubleshoot. These tools interact with the Harvard USPTO Patent Dataset and a new dataset of NeurIPS 2023 papers to solve mathematical, coding, and modeling problems of varying difficulty levels. We demonstrate that LLMs can achieve more reliable and informed problem-solving while maintaining task performance using our framework.

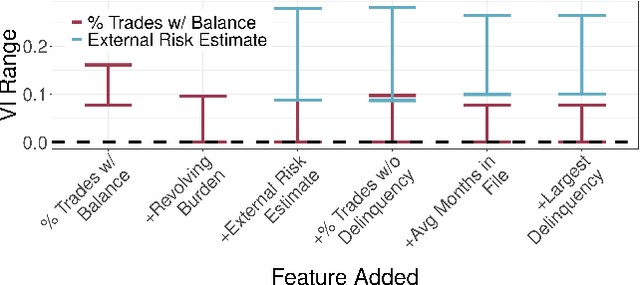
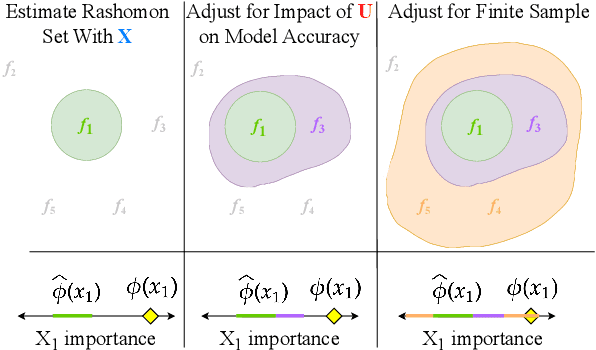
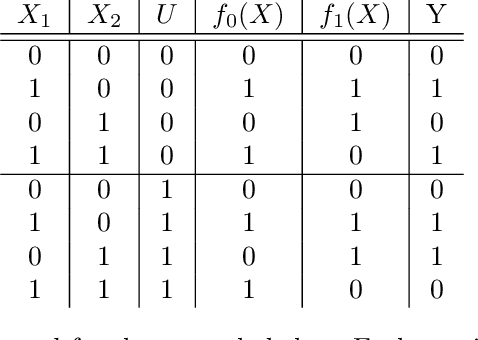
Doctor Rashomon and the UNIVERSE of Madness: Variable Importance with Unobserved Confounding and the Rashomon Effect

Variable importance (VI) methods are often used for hypothesis generation, feature selection, and scientific validation. In the standard VI pipeline, an analyst estimates VI for a single predictive model with only the observed features. However, the importance of a feature depends heavily on which other variables are included in the model, and essential variables are often omitted from observational datasets. Moreover, the VI estimated for one model is often not the same as the VI estimated for another equally-good model - a phenomenon known as the Rashomon Effect. We address these gaps by introducing UNobservables and Inference for Variable importancE using Rashomon SEts (UNIVERSE). Our approach adapts Rashomon sets - the sets of near-optimal models in a dataset - to produce bounds on the true VI even with missing features. We theoretically guarantee the robustness of our approach, show strong performance on semi-synthetic simulations, and demonstrate its utility in a credit risk task.

Leveraging Predictive Equivalence in Decision Trees

Decision trees are widely used for interpretable machine learning due to their clearly structured reasoning process. However, this structure belies a challenge we refer to as predictive equivalence: a given tree's decision boundary can be represented by many different decision trees. The presence of models with identical decision boundaries but different evaluation processes makes model selection challenging. The models will have different variable importance and behave differently in the presence of missing values, but most optimization procedures will arbitrarily choose one such model to return. We present a boolean logical representation of decision trees that does not exhibit predictive equivalence and is faithful to the underlying decision boundary. We apply our representation to several downstream machine learning tasks. Using our representation, we show that decision trees are surprisingly robust to test-time missingness of feature values; we address predictive equivalence's impact on quantifying variable importance; and we present an algorithm to optimize the cost of reaching predictions.

Data Fusion for Partial Identification of Causal Effects

Data fusion techniques integrate information from heterogeneous data sources to improve learning, generalization, and decision making across data sciences. In causal inference, these methods leverage rich observational data to improve causal effect estimation, while maintaining the trustworthiness of randomized controlled trials. Existing approaches often relax the strong no unobserved confounding assumption by instead assuming exchangeability of counterfactual outcomes across data sources. However, when both assumptions simultaneously fail - a common scenario in practice - current methods cannot identify or estimate causal effects. We address this limitation by proposing a novel partial identification framework that enables researchers to answer key questions such as: Is the causal effect positive or negative? and How severe must assumption violations be to overturn this conclusion? Our approach introduces interpretable sensitivity parameters that quantify assumption violations and derives corresponding causal effect bounds. We develop doubly robust estimators for these bounds and operationalize breakdown frontier analysis to understand how causal conclusions change as assumption violations increase. We apply our framework to the Project STAR study, which investigates the effect of classroom size on students' third-grade standardized test performance. Our analysis reveals that the Project STAR results are robust to simultaneous violations of key assumptions, both on average and across various subgroups of interest. This strengthens confidence in the study's conclusions despite potential unmeasured biases in the data.

Rashomon Sets for Prototypical-Part Networks: Editing Interpretable Models in Real-Time

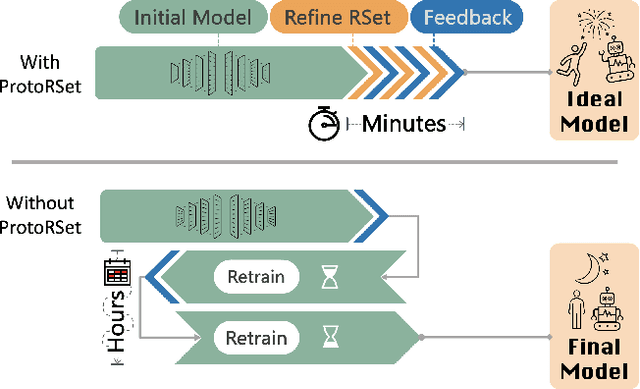
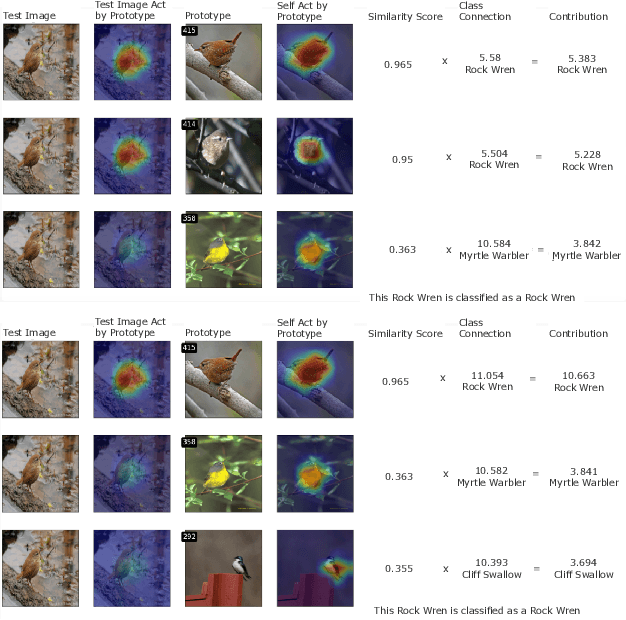
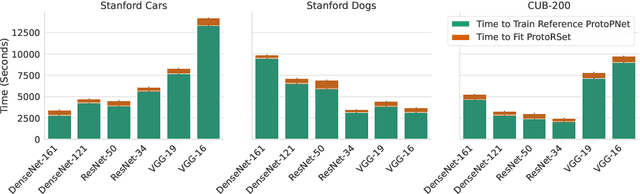
Interpretability is critical for machine learning models in high-stakes settings because it allows users to verify the model's reasoning. In computer vision, prototypical part models (ProtoPNets) have become the dominant model type to meet this need. Users can easily identify flaws in ProtoPNets, but fixing problems in a ProtoPNet requires slow, difficult retraining that is not guaranteed to resolve the issue. This problem is called the "interaction bottleneck." We solve the interaction bottleneck for ProtoPNets by simultaneously finding many equally good ProtoPNets (i.e., a draw from a "Rashomon set"). We show that our framework - called Proto-RSet - quickly produces many accurate, diverse ProtoPNets, allowing users to correct problems in real time while maintaining performance guarantees with respect to the training set. We demonstrate the utility of this method in two settings: 1) removing synthetic bias introduced to a bird identification model and 2) debugging a skin cancer identification model. This tool empowers non-machine-learning experts, such as clinicians or domain experts, to quickly refine and correct machine learning models without repeated retraining by machine learning experts.

Models That Are Interpretable But Not Transparent

Faithful explanations are essential for machine learning models in high-stakes applications. Inherently interpretable models are well-suited for these applications because they naturally provide faithful explanations by revealing their decision logic. However, model designers often need to keep these models proprietary to maintain their value. This creates a tension: we need models that are interpretable--allowing human decision-makers to understand and justify predictions, but not transparent, so that the model's decision boundary is not easily replicated by attackers. Shielding the model's decision boundary is particularly challenging alongside the requirement of completely faithful explanations, since such explanations reveal the true logic of the model for an entire subspace around each query point. This work provides an approach, FaithfulDefense, that creates model explanations for logical models that are completely faithful, yet reveal as little as possible about the decision boundary. FaithfulDefense is based on a maximum set cover formulation, and we provide multiple formulations for it, taking advantage of submodularity.

Near Optimal Decision Trees in a SPLIT Second

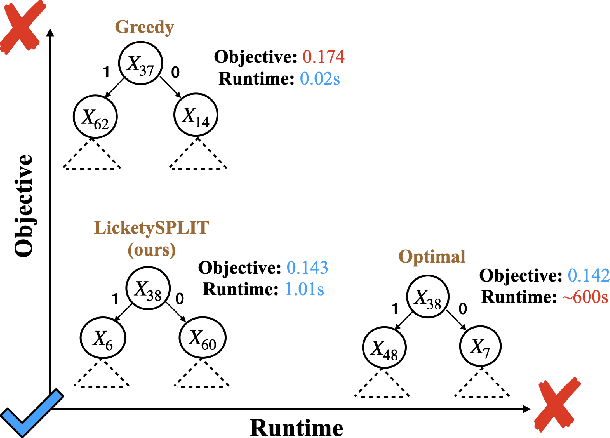
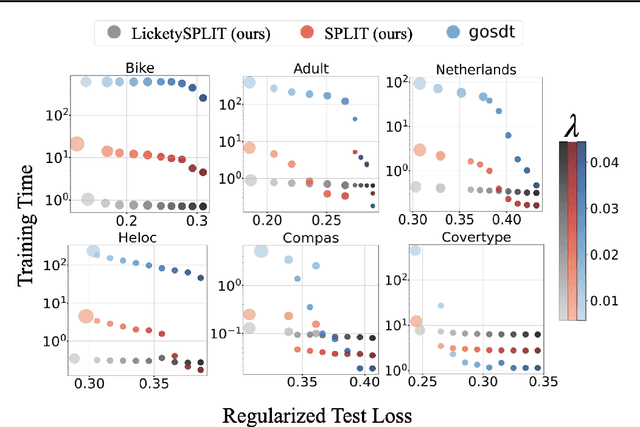
Decision tree optimization is fundamental to interpretable machine learning. The most popular approach is to greedily search for the best feature at every decision point, which is fast but provably suboptimal. Recent approaches find the global optimum using branch and bound with dynamic programming, showing substantial improvements in accuracy and sparsity at great cost to scalability. An ideal solution would have the accuracy of an optimal method and the scalability of a greedy method. We introduce a family of algorithms called SPLIT (SParse Lookahead for Interpretable Trees) that moves us significantly forward in achieving this ideal balance. We demonstrate that not all sub-problems need to be solved to optimality to find high quality trees; greediness suffices near the leaves. Since each depth adds an exponential number of possible trees, this change makes our algorithms orders of magnitude faster than existing optimal methods, with negligible loss in performance. We extend this algorithm to allow scalable computation of sets of near-optimal trees (i.e., the Rashomon set).