Rashomon Sets for Prototypical-Part Networks: Editing Interpretable Models in Real-Time

Interpretability is critical for machine learning models in high-stakes settings because it allows users to verify the model's reasoning. In computer vision, prototypical part models (ProtoPNets) have become the dominant model type to meet this need. Users can easily identify flaws in ProtoPNets, but fixing problems in a ProtoPNet requires slow, difficult retraining that is not guaranteed to resolve the issue. This problem is called the "interaction bottleneck." We solve the interaction bottleneck for ProtoPNets by simultaneously finding many equally good ProtoPNets (i.e., a draw from a "Rashomon set"). We show that our framework - called Proto-RSet - quickly produces many accurate, diverse ProtoPNets, allowing users to correct problems in real time while maintaining performance guarantees with respect to the training set. We demonstrate the utility of this method in two settings: 1) removing synthetic bias introduced to a bird identification model and 2) debugging a skin cancer identification model. This tool empowers non-machine-learning experts, such as clinicians or domain experts, to quickly refine and correct machine learning models without repeated retraining by machine learning experts.

Near Optimal Decision Trees in a SPLIT Second

Decision tree optimization is fundamental to interpretable machine learning. The most popular approach is to greedily search for the best feature at every decision point, which is fast but provably suboptimal. Recent approaches find the global optimum using branch and bound with dynamic programming, showing substantial improvements in accuracy and sparsity at great cost to scalability. An ideal solution would have the accuracy of an optimal method and the scalability of a greedy method. We introduce a family of algorithms called SPLIT (SParse Lookahead for Interpretable Trees) that moves us significantly forward in achieving this ideal balance. We demonstrate that not all sub-problems need to be solved to optimality to find high quality trees; greediness suffices near the leaves. Since each depth adds an exponential number of possible trees, this change makes our algorithms orders of magnitude faster than existing optimal methods, with negligible loss in performance. We extend this algorithm to allow scalable computation of sets of near-optimal trees (i.e., the Rashomon set).

Interpretable Generalized Additive Models for Datasets with Missing Values

Many important datasets contain samples that are missing one or more feature values. Maintaining the interpretability of machine learning models in the presence of such missing data is challenging. Singly or multiply imputing missing values complicates the model's mapping from features to labels. On the other hand, reasoning on indicator variables that represent missingness introduces a potentially large number of additional terms, sacrificing sparsity. We solve these problems with M-GAM, a sparse, generalized, additive modeling approach that incorporates missingness indicators and their interaction terms while maintaining sparsity through l0 regularization. We show that M-GAM provides similar or superior accuracy to prior methods while significantly improving sparsity relative to either imputation or naive inclusion of indicator variables.

Fast Sparse Decision Tree Optimization via Reference Ensembles

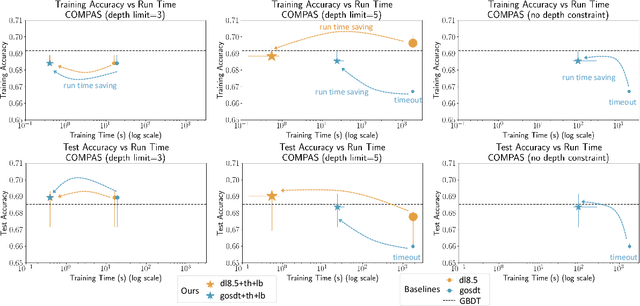
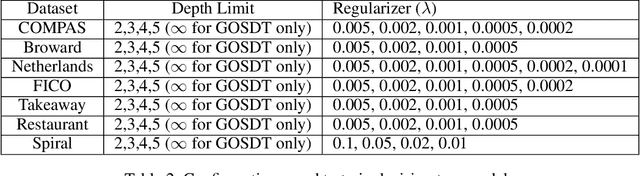
Sparse decision tree optimization has been one of the most fundamental problems in AI since its inception and is a challenge at the core of interpretable machine learning. Sparse decision tree optimization is computationally hard, and despite steady effort since the 1960's, breakthroughs have only been made on the problem within the past few years, primarily on the problem of finding optimal sparse decision trees. However, current state-of-the-art algorithms often require impractical amounts of computation time and memory to find optimal or near-optimal trees for some real-world datasets, particularly those having several continuous-valued features. Given that the search spaces of these decision tree optimization problems are massive, can we practically hope to find a sparse decision tree that competes in accuracy with a black box machine learning model? We address this problem via smart guessing strategies that can be applied to any optimal branch-and-bound-based decision tree algorithm. We show that by using these guesses, we can reduce the run time by multiple orders of magnitude, while providing bounds on how far the resulting trees can deviate from the black box's accuracy and expressive power. Our approach enables guesses about how to bin continuous features, the size of the tree, and lower bounds on the error for the optimal decision tree. Our experiments show that in many cases we can rapidly construct sparse decision trees that match the accuracy of black box models. To summarize: when you are having trouble optimizing, just guess.