Near Optimal Decision Trees in a SPLIT Second
Paper and Code
Feb 21, 2025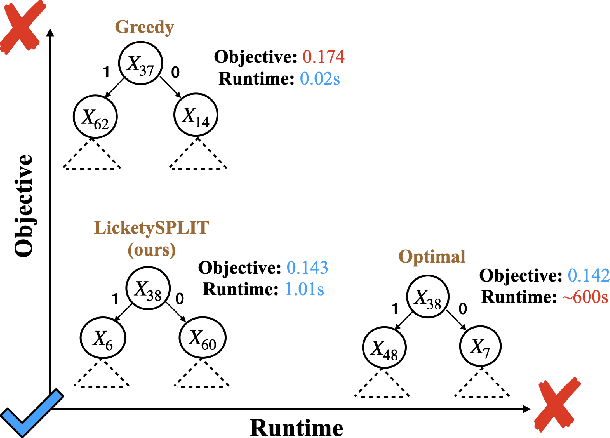

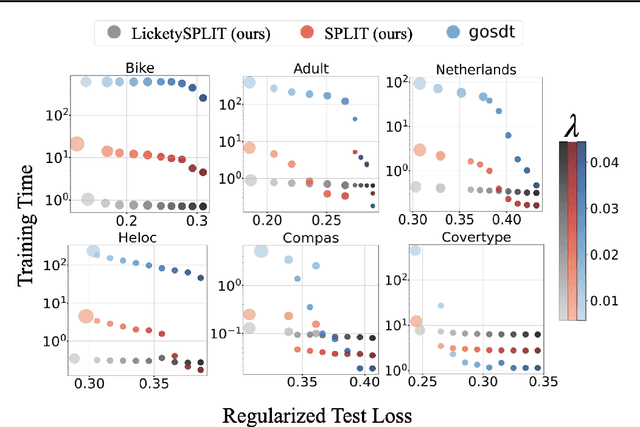

Decision tree optimization is fundamental to interpretable machine learning. The most popular approach is to greedily search for the best feature at every decision point, which is fast but provably suboptimal. Recent approaches find the global optimum using branch and bound with dynamic programming, showing substantial improvements in accuracy and sparsity at great cost to scalability. An ideal solution would have the accuracy of an optimal method and the scalability of a greedy method. We introduce a family of algorithms called SPLIT (SParse Lookahead for Interpretable Trees) that moves us significantly forward in achieving this ideal balance. We demonstrate that not all sub-problems need to be solved to optimality to find high quality trees; greediness suffices near the leaves. Since each depth adds an exponential number of possible trees, this change makes our algorithms orders of magnitude faster than existing optimal methods, with negligible loss in performance. We extend this algorithm to allow scalable computation of sets of near-optimal trees (i.e., the Rashomon set).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge