$e^{\text{RPCA}}$: Robust Principal Component Analysis for Exponential Family Distributions

Robust Principal Component Analysis (RPCA) is a widely used method for recovering low-rank structure from data matrices corrupted by significant and sparse outliers. These corruptions may arise from occlusions, malicious tampering, or other causes for anomalies, and the joint identification of such corruptions with low-rank background is critical for process monitoring and diagnosis. However, existing RPCA methods and their extensions largely do not account for the underlying probabilistic distribution for the data matrices, which in many applications are known and can be highly non-Gaussian. We thus propose a new method called Robust Principal Component Analysis for Exponential Family distributions ($e^{\text{RPCA}}$), which can perform the desired decomposition into low-rank and sparse matrices when such a distribution falls within the exponential family. We present a novel alternating direction method of multiplier optimization algorithm for efficient $e^{\text{RPCA}}$ decomposition. The effectiveness of $e^{\text{RPCA}}$ is then demonstrated in two applications: the first for steel sheet defect detection, and the second for crime activity monitoring in the Atlanta metropolitan area.

PERCEPT: a new online change-point detection method using topological data analysis

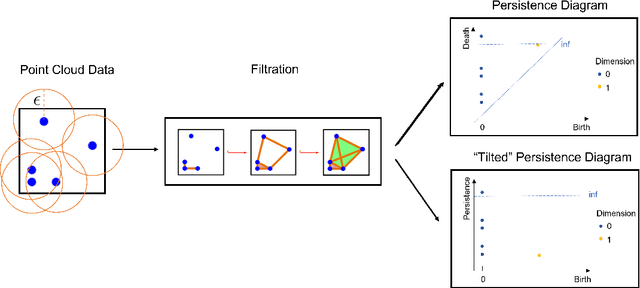
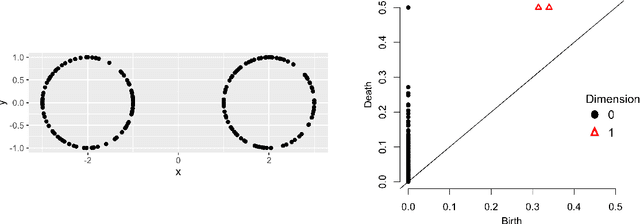
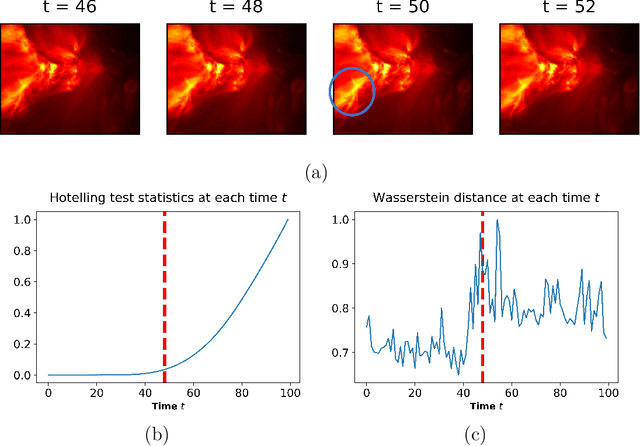
Topological data analysis (TDA) provides a set of data analysis tools for extracting embedded topological structures from complex high-dimensional datasets. In recent years, TDA has been a rapidly growing field which has found success in a wide range of applications, including signal processing, neuroscience and network analysis. In these applications, the online detection of changes is of crucial importance, but this can be highly challenging since such changes often occur in a low-dimensional embedding within high-dimensional data streams. We thus propose a new method, called PERsistence diagram-based ChangE-PoinT detection (PERCEPT), which leverages the learned topological structure from TDA to sequentially detect changes. PERCEPT follows two key steps: it first learns the embedded topology as a point cloud via persistence diagrams, then applies a non-parametric monitoring approach for detecting changes in the resulting point cloud distributions. This yields a non-parametric, topology-aware framework which can efficiently detect online changes from high-dimensional data streams. We investigate the effectiveness of PERCEPT over existing methods in a suite of numerical experiments where the data streams have an embedded topological structure. We then demonstrate the usefulness of PERCEPT in two applications in solar flare monitoring and human gesture detection.