Position Paper: Bayesian Deep Learning in the Age of Large-Scale AI

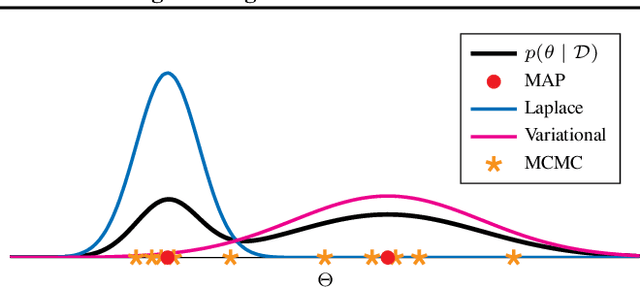
In the current landscape of deep learning research, there is a predominant emphasis on achieving high predictive accuracy in supervised tasks involving large image and language datasets. However, a broader perspective reveals a multitude of overlooked metrics, tasks, and data types, such as uncertainty, active and continual learning, and scientific data, that demand attention. Bayesian deep learning (BDL) constitutes a promising avenue, offering advantages across these diverse settings. This paper posits that BDL can elevate the capabilities of deep learning. It revisits the strengths of BDL, acknowledges existing challenges, and highlights some exciting research avenues aimed at addressing these obstacles. Looking ahead, the discussion focuses on possible ways to combine large-scale foundation models with BDL to unlock their full potential.

Spectral Gap Regularization of Neural Networks

We introduce Fiedler regularization, a novel approach for regularizing neural networks that utilizes spectral/graphical information. Existing regularization methods often focus on penalizing weights in a global/uniform manner that ignores the connectivity structure of the neural network. We propose to use the Fiedler value of the neural network's underlying graph as a tool for regularization. We provide theoretical motivation for this approach via spectral graph theory. We demonstrate several useful properties of the Fiedler value that make it useful as a regularization tool. We provide an approximate, variational approach for faster computation during training. We provide an alternative formulation of this framework in the form of a structurally weighted $\text{L}_1$ penalty, thus linking our approach to sparsity induction. We provide uniform generalization error bounds for Fiedler regularization via a Rademacher complexity analysis. We performed experiments on datasets that compare Fiedler regularization with classical regularization methods such as dropout and weight decay. Results demonstrate the efficacy of Fiedler regularization. This is a journal extension of the conference paper by Tam and Dunson (2020).

Hierarchical shrinkage Gaussian processes: applications to computer code emulation and dynamical system recovery

In many areas of science and engineering, computer simulations are widely used as proxies for physical experiments, which can be infeasible or unethical. Such simulations can often be computationally expensive, and an emulator can be trained to efficiently predict the desired response surface. A widely-used emulator is the Gaussian process (GP), which provides a flexible framework for efficient prediction and uncertainty quantification. Standard GPs, however, do not capture structured sparsity on the underlying response surface, which is present in many applications, particularly in the physical sciences. We thus propose a new hierarchical shrinkage GP (HierGP), which incorporates such structure via cumulative shrinkage priors within a GP framework. We show that the HierGP implicitly embeds the well-known principles of effect sparsity, heredity and hierarchy for analysis of experiments, which allows our model to identify structured sparse features from the response surface with limited data. We propose efficient posterior sampling algorithms for model training and prediction, and prove desirable consistency properties for the HierGP. Finally, we demonstrate the improved performance of HierGP over existing models, in a suite of numerical experiments and an application to dynamical system recovery.

Multiscale Graph Comparison via the Embedded Laplacian Distance

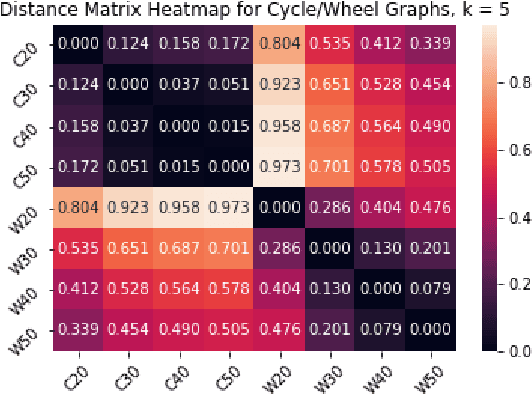
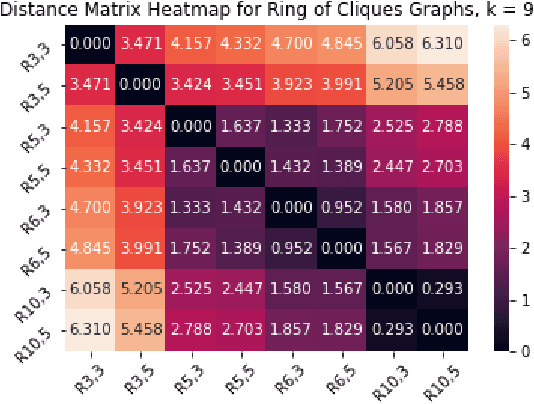
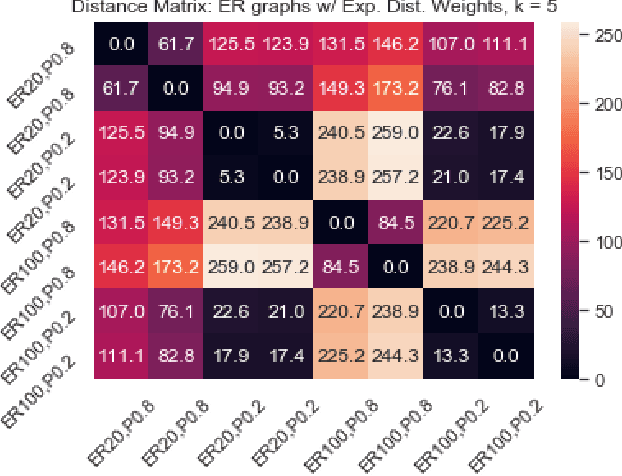
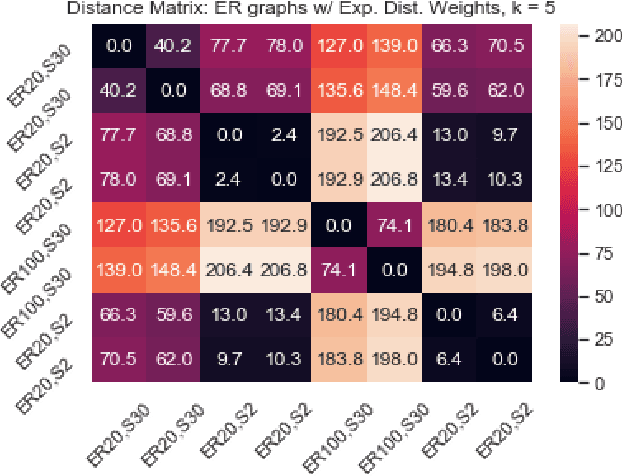
We introduce a simple and fast method for comparing graphs of different sizes. Existing approaches are often either limited to comparing graphs with the same number of vertices or are computationally unscalable. We propose the Embedded Laplacian Distance (ELD) for comparing graphs of potentially vastly different sizes. Our approach first projects the graphs onto a common, low-dimensional Laplacian embedding space that respects graphical structure. This reduces the problem to that of comparing point clouds in a Euclidean space. A distance can then be computed efficiently via a natural sliced Wasserstein approach. We show that the ELD is a pseudo-metric and is invariant under graph isomorphism. We provide intuitive interpretations of the ELD using tools from spectral graph theory. We test the efficacy of the ELD approach extensively on both simulated and real data. Results obtained are excellent.

Gaussian Process Subspace Regression for Model Reduction

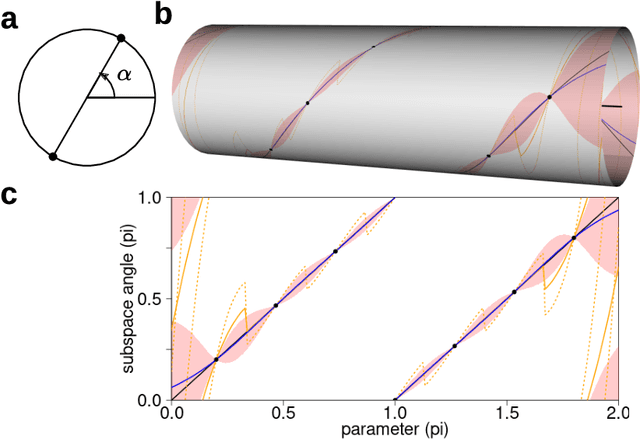
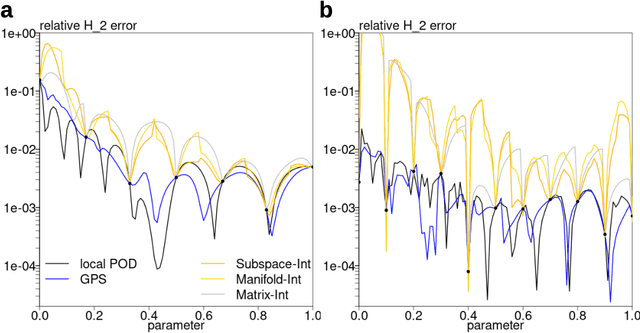
Subspace-valued functions arise in a wide range of problems, including parametric reduced order modeling (PROM). In PROM, each parameter point can be associated with a subspace, which is used for Petrov-Galerkin projections of large system matrices. Previous efforts to approximate such functions use interpolations on manifolds, which can be inaccurate and slow. To tackle this, we propose a novel Bayesian nonparametric model for subspace prediction: the Gaussian Process Subspace regression (GPS) model. This method is extrinsic and intrinsic at the same time: with multivariate Gaussian distributions on the Euclidean space, it induces a joint probability model on the Grassmann manifold, the set of fixed-dimensional subspaces. The GPS adopts a simple yet general correlation structure, and a principled approach for model selection. Its predictive distribution admits an analytical form, which allows for efficient subspace prediction over the parameter space. For PROM, the GPS provides a probabilistic prediction at a new parameter point that retains the accuracy of local reduced models, at a computational complexity that does not depend on system dimension, and thus is suitable for online computation. We give four numerical examples to compare our method to subspace interpolation, as well as two methods that interpolate local reduced models. Overall, GPS is the most data efficient, more computationally efficient than subspace interpolation, and gives smooth predictions with uncertainty quantification.

Statistical Guarantees for Transformation Based Models with Applications to Implicit Variational Inference

Transformation-based methods have been an attractive approach in non-parametric inference for problems such as unconditional and conditional density estimation due to their unique hierarchical structure that models the data as flexible transformation of a set of common latent variables. More recently, transformation-based models have been used in variational inference (VI) to construct flexible implicit families of variational distributions. However, their use in both non-parametric inference and variational inference lacks theoretical justification. We provide theoretical justification for the use of non-linear latent variable models (NL-LVMs) in non-parametric inference by showing that the support of the transformation induced prior in the space of densities is sufficiently large in the $L_1$ sense. We also show that, when a Gaussian process (GP) prior is placed on the transformation function, the posterior concentrates at the optimal rate up to a logarithmic factor. Adopting the flexibility demonstrated in the non-parametric setting, we use the NL-LVM to construct an implicit family of variational distributions, deemed GP-IVI. We delineate sufficient conditions under which GP-IVI achieves optimal risk bounds and approximates the true posterior in the sense of the Kullback-Leibler divergence. To the best of our knowledge, this is the first work on providing theoretical guarantees for implicit variational inference.

Principal Ellipsoid Analysis (PEA): Efficient non-linear dimension reduction & clustering

Even with the rise in popularity of over-parameterized models, simple dimensionality reduction and clustering methods, such as PCA and k-means, are still routinely used in an amazing variety of settings. A primary reason is the combination of simplicity, interpretability and computational efficiency. The focus of this article is on improving upon PCA and k-means, by allowing non-linear relations in the data and more flexible cluster shapes, without sacrificing the key advantages. The key contribution is a new framework for Principal Elliptical Analysis (PEA), defining a simple and computationally efficient alternative to PCA that fits the best elliptical approximation through the data. We provide theoretical guarantees on the proposed PEA algorithm using Vapnik-Chervonenkis (VC) theory to show strong consistency and uniform concentration bounds. Toy experiments illustrate the performance of PEA, and the ability to adapt to non-linear structure and complex cluster shapes. In a rich variety of real data clustering applications, PEA is shown to do as well as k-means for simple datasets, while dramatically improving performance in more complex settings.

Bayesian neural networks and dimensionality reduction

In conducting non-linear dimensionality reduction and feature learning, it is common to suppose that the data lie near a lower-dimensional manifold. A class of model-based approaches for such problems includes latent variables in an unknown non-linear regression function; this includes Gaussian process latent variable models and variational auto-encoders (VAEs) as special cases. VAEs are artificial neural networks (ANNs) that employ approximations to make computation tractable; however, current implementations lack adequate uncertainty quantification in estimating the parameters, predictive densities, and lower-dimensional subspace, and can be unstable and lack interpretability in practice. We attempt to solve these problems by deploying Markov chain Monte Carlo sampling algorithms (MCMC) for Bayesian inference in ANN models with latent variables. We address issues of identifiability by imposing constraints on the ANN parameters as well as by using anchor points. This is demonstrated on simulated and real data examples. We find that current MCMC sampling schemes face fundamental challenges in neural networks involving latent variables, motivating new research directions.

Supervised Autoencoders Learn Robust Joint Factor Models of Neural Activity

Factor models are routinely used for dimensionality reduction in modeling of correlated, high-dimensional data. We are particularly motivated by neuroscience applications collecting high-dimensional `predictors' corresponding to brain activity in different regions along with behavioral outcomes. Joint factor models for the predictors and outcomes are natural, but maximum likelihood estimates of these models can struggle in practice when there is model misspecification. We propose an alternative inference strategy based on supervised autoencoders; rather than placing a probability distribution on the latent factors, we define them as an unknown function of the high-dimensional predictors. This mapping function, along with the loadings, can be optimized to explain variance in brain activity while simultaneously being predictive of behavior. In practice, the mapping function can range in complexity from linear to more complex forms, such as splines or neural networks, with the usual tradeoff between bias and variance. This approach yields distinct solutions from a maximum likelihood inference strategy, as we demonstrate by deriving analytic solutions for a linear Gaussian factor model. Using synthetic data, we show that this function-based approach is robust against multiple types of misspecification. We then apply this technique to a neuroscience application resulting in substantial gains in predicting behavioral tasks from electrophysiological measurements in multiple factor models.

Fiedler Regularization: Learning Neural Networks with Graph Sparsity

We introduce a novel regularization approach for deep learning that incorporates and respects the underlying graphical structure of the neural network. Existing regularization methods often focus on dropping/penalizing weights in a global manner that ignores the connectivity structure of the neural network. We propose to use the Fiedler value of the neural network's underlying graph as a tool for regularization. We provide theoretical support for this approach via spectral graph theory. We demonstrate the convexity of this penalty and provide an approximate, variational approach for fast computation in practical training of neural networks. We provide bounds on such approximations. We provide an alternative but equivalent formulation of this framework in the form of a structurally weighted L1 penalty, thus linking our approach to sparsity induction. We performed experiments on datasets that compare Fiedler regularization with traditional regularization methods such as dropout and weight decay. Results demonstrate the efficacy of Fiedler regularization.