Natural Variational Annealing for Multimodal Optimization

We introduce a new multimodal optimization approach called Natural Variational Annealing (NVA) that combines the strengths of three foundational concepts to simultaneously search for multiple global and local modes of black-box nonconvex objectives. First, it implements a simultaneous search by using variational posteriors, such as, mixtures of Gaussians. Second, it applies annealing to gradually trade off exploration for exploitation. Finally, it learns the variational search distribution using natural-gradient learning where updates resemble well-known and easy-to-implement algorithms. The three concepts come together in NVA giving rise to new algorithms and also allowing us to incorporate "fitness shaping", a core concept from evolutionary algorithms. We assess the quality of search on simulations and compare them to methods using gradient descent and evolution strategies. We also provide an application to a real-world inverse problem in planetary science.

Logarithmic Regret for Unconstrained Submodular Maximization Stochastic Bandit

We address the online unconstrained submodular maximization problem (Online USM), in a setting with stochastic bandit feedback. In this framework, a decision-maker receives noisy rewards from a nonmonotone submodular function, taking values in a known bounded interval. This paper proposes Double-Greedy - Explore-then-Commit (DG-ETC), adapting the Double-Greedy approach from the offline and online full-information settings. DG-ETC satisfies a O(d log(dT)) problemdependent upper bound for the 1/2-approximate pseudo-regret, as well as a O(dT^{2/3}log(dT)^{1/3}) problem-free one at the same time, outperforming existing approaches. To that end, we introduce a notion of hardness for submodular functions, characterizing how difficult it is to maximize them with this type of strategy.

Just rotate it! Uncertainty estimation in closed-source models via multiple queries

We propose a simple and effective method to estimate the uncertainty of closed-source deep neural network image classification models. Given a base image, our method creates multiple transformed versions and uses them to query the top-1 prediction of the closed-source model. We demonstrate significant improvements in the calibration of uncertainty estimates compared to the naive baseline of assigning 100\% confidence to all predictions. While we initially explore Gaussian perturbations, our empirical findings indicate that natural transformations, such as rotations and elastic deformations, yield even better-calibrated predictions. Furthermore, through empirical results and a straightforward theoretical analysis, we elucidate the reasons behind the superior performance of natural transformations over Gaussian noise. Leveraging these insights, we propose a transfer learning approach that further improves our calibration results.

Covariance-Adaptive Least-Squares Algorithm for Stochastic Combinatorial Semi-Bandits

We address the problem of stochastic combinatorial semi-bandits, where a player can select from P subsets of a set containing d base items. Most existing algorithms (e.g. CUCB, ESCB, OLS-UCB) require prior knowledge on the reward distribution, like an upper bound on a sub-Gaussian proxy-variance, which is hard to estimate tightly. In this work, we design a variance-adaptive version of OLS-UCB, relying on an online estimation of the covariance structure. Estimating the coefficients of a covariance matrix is much more manageable in practical settings and results in improved regret upper bounds compared to proxy variance-based algorithms. When covariance coefficients are all non-negative, we show that our approach efficiently leverages the semi-bandit feedback and provably outperforms bandit feedback approaches, not only in exponential regimes where P $\gg$ d but also when P $\le$ d, which is not straightforward from most existing analyses.

Position Paper: Bayesian Deep Learning in the Age of Large-Scale AI

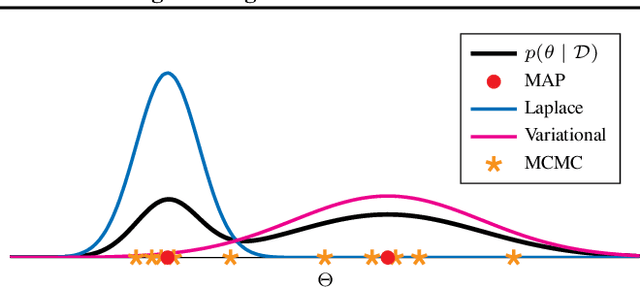
In the current landscape of deep learning research, there is a predominant emphasis on achieving high predictive accuracy in supervised tasks involving large image and language datasets. However, a broader perspective reveals a multitude of overlooked metrics, tasks, and data types, such as uncertainty, active and continual learning, and scientific data, that demand attention. Bayesian deep learning (BDL) constitutes a promising avenue, offering advantages across these diverse settings. This paper posits that BDL can elevate the capabilities of deep learning. It revisits the strengths of BDL, acknowledges existing challenges, and highlights some exciting research avenues aimed at addressing these obstacles. Looking ahead, the discussion focuses on possible ways to combine large-scale foundation models with BDL to unlock their full potential.

Efficient Neural Networks for Tiny Machine Learning: A Comprehensive Review

The field of Tiny Machine Learning (TinyML) has gained significant attention due to its potential to enable intelligent applications on resource-constrained devices. This review provides an in-depth analysis of the advancements in efficient neural networks and the deployment of deep learning models on ultra-low power microcontrollers (MCUs) for TinyML applications. It begins by introducing neural networks and discussing their architectures and resource requirements. It then explores MEMS-based applications on ultra-low power MCUs, highlighting their potential for enabling TinyML on resource-constrained devices. The core of the review centres on efficient neural networks for TinyML. It covers techniques such as model compression, quantization, and low-rank factorization, which optimize neural network architectures for minimal resource utilization on MCUs. The paper then delves into the deployment of deep learning models on ultra-low power MCUs, addressing challenges such as limited computational capabilities and memory resources. Techniques like model pruning, hardware acceleration, and algorithm-architecture co-design are discussed as strategies to enable efficient deployment. Lastly, the review provides an overview of current limitations in the field, including the trade-off between model complexity and resource constraints. Overall, this review paper presents a comprehensive analysis of efficient neural networks and deployment strategies for TinyML on ultra-low-power MCUs. It identifies future research directions for unlocking the full potential of TinyML applications on resource-constrained devices.

Something for (almost) nothing: Improving deep ensemble calibration using unlabeled data

We present a method to improve the calibration of deep ensembles in the small training data regime in the presence of unlabeled data. Our approach is extremely simple to implement: given an unlabeled set, for each unlabeled data point, we simply fit a different randomly selected label with each ensemble member. We provide a theoretical analysis based on a PAC-Bayes bound which guarantees that if we fit such a labeling on unlabeled data, and the true labels on the training data, we obtain low negative log-likelihood and high ensemble diversity on testing samples. Empirically, through detailed experiments, we find that for low to moderately-sized training sets, our ensembles are more diverse and provide better calibration than standard ensembles, sometimes significantly.

A Primer on Bayesian Neural Networks: Review and Debates

Neural networks have achieved remarkable performance across various problem domains, but their widespread applicability is hindered by inherent limitations such as overconfidence in predictions, lack of interpretability, and vulnerability to adversarial attacks. To address these challenges, Bayesian neural networks (BNNs) have emerged as a compelling extension of conventional neural networks, integrating uncertainty estimation into their predictive capabilities. This comprehensive primer presents a systematic introduction to the fundamental concepts of neural networks and Bayesian inference, elucidating their synergistic integration for the development of BNNs. The target audience comprises statisticians with a potential background in Bayesian methods but lacking deep learning expertise, as well as machine learners proficient in deep neural networks but with limited exposure to Bayesian statistics. We provide an overview of commonly employed priors, examining their impact on model behavior and performance. Additionally, we delve into the practical considerations associated with training and inference in BNNs. Furthermore, we explore advanced topics within the realm of BNN research, acknowledging the existence of ongoing debates and controversies. By offering insights into cutting-edge developments, this primer not only equips researchers and practitioners with a solid foundation in BNNs, but also illuminates the potential applications of this dynamic field. As a valuable resource, it fosters an understanding of BNNs and their promising prospects, facilitating further advancements in the pursuit of knowledge and innovation.

The fine print on tempered posteriors

We conduct a detailed investigation of tempered posteriors and uncover a number of crucial and previously undiscussed points. Contrary to previous results, we first show that for realistic models and datasets and the tightly controlled case of the Laplace approximation to the posterior, stochasticity does not in general improve test accuracy. The coldest temperature is often optimal. One might think that Bayesian models with some stochasticity can at least obtain improvements in terms of calibration. However, we show empirically that when gains are obtained this comes at the cost of degradation in test accuracy. We then discuss how targeting Frequentist metrics using Bayesian models provides a simple explanation of the need for a temperature parameter $\lambda$ in the optimization objective. Contrary to prior works, we finally show through a PAC-Bayesian analysis that the temperature $\lambda$ cannot be seen as simply fixing a misspecified prior or likelihood.

Hybrids of Constraint-based and Noise-based Algorithms for Causal Discovery from Time Series

Constraint-based and noise-based methods have been proposed to discover summary causal graphs from observational time series under strong assumptions which can be violated or impossible to verify in real applications. Recently, a hybrid method (Assaad et al, 2021) that combines these two approaches, proved to be robust to assumption violation. However, this method assumes that the summary causal graph is acyclic, but cycles are common in many applications. For example, in ecological communities, there may be cyclic relationships between predator and prey populations, creating feedback loops. Therefore, this paper presents two new frameworks for hybrids of constraint-based and noise-based methods that can discover summary causal graphs that may or may not contain cycles. For each framework, we provide two hybrid algorithms which are experimentally tested on simulated data, realistic ecological data, and real data from various applications. Experiments show that our hybrid approaches are robust and yield good results over most datasets.