Just rotate it! Uncertainty estimation in closed-source models via multiple queries

We propose a simple and effective method to estimate the uncertainty of closed-source deep neural network image classification models. Given a base image, our method creates multiple transformed versions and uses them to query the top-1 prediction of the closed-source model. We demonstrate significant improvements in the calibration of uncertainty estimates compared to the naive baseline of assigning 100\% confidence to all predictions. While we initially explore Gaussian perturbations, our empirical findings indicate that natural transformations, such as rotations and elastic deformations, yield even better-calibrated predictions. Furthermore, through empirical results and a straightforward theoretical analysis, we elucidate the reasons behind the superior performance of natural transformations over Gaussian noise. Leveraging these insights, we propose a transfer learning approach that further improves our calibration results.

Just rephrase it! Uncertainty estimation in closed-source language models via multiple rephrased queries

State-of-the-art large language models are sometimes distributed as open-source software but are also increasingly provided as a closed-source service. These closed-source large-language models typically see the widest usage by the public, however, they often do not provide an estimate of their uncertainty when responding to queries. As even the best models are prone to ``hallucinating" false information with high confidence, a lack of a reliable estimate of uncertainty limits the applicability of these models in critical settings. We explore estimating the uncertainty of closed-source LLMs via multiple rephrasings of an original base query. Specifically, we ask the model, multiple rephrased questions, and use the similarity of the answers as an estimate of uncertainty. We diverge from previous work in i) providing rules for rephrasing that are simple to memorize and use in practice ii) proposing a theoretical framework for why multiple rephrased queries obtain calibrated uncertainty estimates. Our method demonstrates significant improvements in the calibration of uncertainty estimates compared to the baseline and provides intuition as to how query strategies should be designed for optimal test calibration.

Something for (almost) nothing: Improving deep ensemble calibration using unlabeled data

We present a method to improve the calibration of deep ensembles in the small training data regime in the presence of unlabeled data. Our approach is extremely simple to implement: given an unlabeled set, for each unlabeled data point, we simply fit a different randomly selected label with each ensemble member. We provide a theoretical analysis based on a PAC-Bayes bound which guarantees that if we fit such a labeling on unlabeled data, and the true labels on the training data, we obtain low negative log-likelihood and high ensemble diversity on testing samples. Empirically, through detailed experiments, we find that for low to moderately-sized training sets, our ensembles are more diverse and provide better calibration than standard ensembles, sometimes significantly.

A Primer on Bayesian Neural Networks: Review and Debates

Neural networks have achieved remarkable performance across various problem domains, but their widespread applicability is hindered by inherent limitations such as overconfidence in predictions, lack of interpretability, and vulnerability to adversarial attacks. To address these challenges, Bayesian neural networks (BNNs) have emerged as a compelling extension of conventional neural networks, integrating uncertainty estimation into their predictive capabilities. This comprehensive primer presents a systematic introduction to the fundamental concepts of neural networks and Bayesian inference, elucidating their synergistic integration for the development of BNNs. The target audience comprises statisticians with a potential background in Bayesian methods but lacking deep learning expertise, as well as machine learners proficient in deep neural networks but with limited exposure to Bayesian statistics. We provide an overview of commonly employed priors, examining their impact on model behavior and performance. Additionally, we delve into the practical considerations associated with training and inference in BNNs. Furthermore, we explore advanced topics within the realm of BNN research, acknowledging the existence of ongoing debates and controversies. By offering insights into cutting-edge developments, this primer not only equips researchers and practitioners with a solid foundation in BNNs, but also illuminates the potential applications of this dynamic field. As a valuable resource, it fosters an understanding of BNNs and their promising prospects, facilitating further advancements in the pursuit of knowledge and innovation.

The fine print on tempered posteriors

We conduct a detailed investigation of tempered posteriors and uncover a number of crucial and previously undiscussed points. Contrary to previous results, we first show that for realistic models and datasets and the tightly controlled case of the Laplace approximation to the posterior, stochasticity does not in general improve test accuracy. The coldest temperature is often optimal. One might think that Bayesian models with some stochasticity can at least obtain improvements in terms of calibration. However, we show empirically that when gains are obtained this comes at the cost of degradation in test accuracy. We then discuss how targeting Frequentist metrics using Bayesian models provides a simple explanation of the need for a temperature parameter $\lambda$ in the optimization objective. Contrary to prior works, we finally show through a PAC-Bayesian analysis that the temperature $\lambda$ cannot be seen as simply fixing a misspecified prior or likelihood.

Europepolls: A Dataset of Country-Level Opinion Polling Data for the European Union and the UK

I propose an open dataset of country-level historical opinion polling data for the European Union and the UK. The dataset aims to fill a gap in available opinion polling data for the European Union. Some existing datasets are restricted to the past five years, limiting research opportunities. At the same time, some larger proprietary datasets exist but are available only in a visual preprocessed time series format. Finally, while other large datasets for individual countries might exist, these could be inaccessible due to language barriers. The data was gathered from Wikipedia, and preprocessed using the pandas library. Both the raw and the preprocessed data are in the .csv format. I hope that given the recent advances in LLMs and deep learning in general, this large dataset will enable researchers to uncover complex interactions between multimodal data (news articles, economic indicators, social media) and voting behavior. The raw data, the preprocessed data, and the preprocessing scripts are available on GitHub.

Cold Posteriors through PAC-Bayes

We investigate the cold posterior effect through the lens of PAC-Bayes generalization bounds. We argue that in the non-asymptotic setting, when the number of training samples is (relatively) small, discussions of the cold posterior effect should take into account that approximate Bayesian inference does not readily provide guarantees of performance on out-of-sample data. Instead, out-of-sample error is better described through a generalization bound. In this context, we explore the connections between the ELBO objective from variational inference and the PAC-Bayes objectives. We note that, while the ELBO and PAC-Bayes objectives are similar, the latter objectives naturally contain a temperature parameter $\lambda$ which is not restricted to be $\lambda=1$. For both regression and classification tasks, in the case of isotropic Laplace approximations to the posterior, we show how this PAC-Bayesian interpretation of the temperature parameter captures the cold posterior effect.

Better PAC-Bayes Bounds for Deep Neural Networks using the Loss Curvature

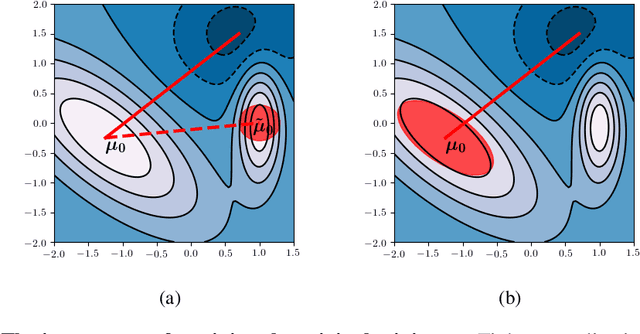
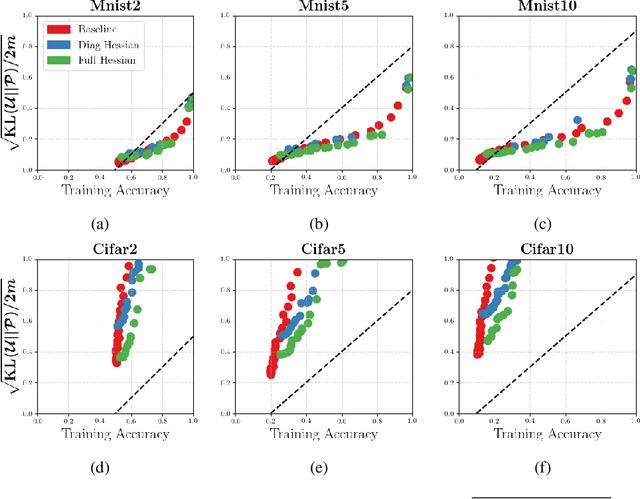
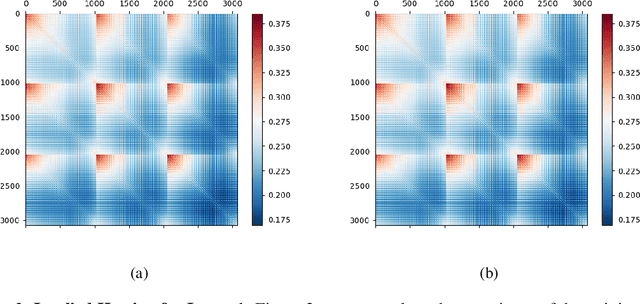
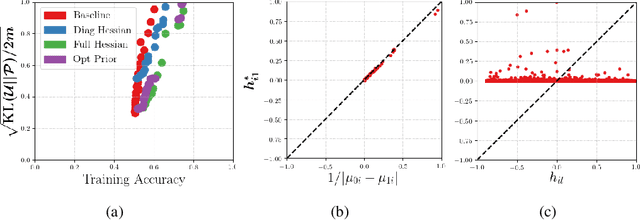
We investigate whether it's possible to tighten PAC-Bayes bounds for deep neural networks by utilizing the Hessian of the training loss at the minimum. For the case of Gaussian priors and posteriors we introduce a Hessian-based method to obtain tighter PAC-Bayes bounds that relies on closed form solutions of layerwise subproblems. We thus avoid commonly used variational inference techniques which can be difficult to implement and time consuming for modern deep architectures. Through careful experiments we analyze the influence of the prior mean, prior covariance, posterior mean and posterior covariance on obtaining tighter bounds. We discuss several limitations in further improving PAC-Bayes bounds through more informative priors.

Some limitations of norm based generalization bounds in deep neural networks

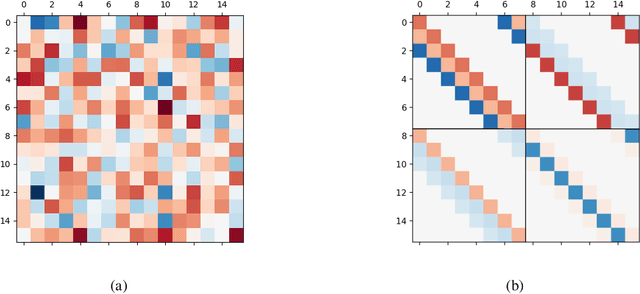
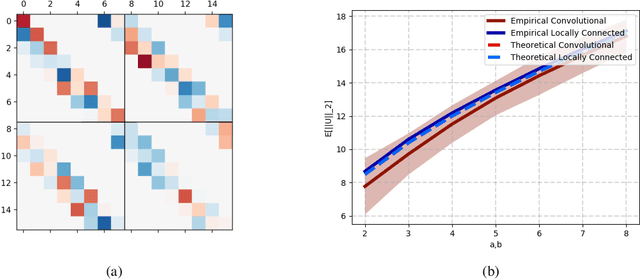
Deep convolutional neural networks have been shown to be able to fit a labeling over random data while still being able to generalize well on normal datasets. Describing deep convolutional neural network capacity through the measure of spectral complexity has been recently proposed to tackle this apparent paradox. Spectral complexity correlates with GE and can distinguish networks trained on normal and random labels. We propose the first GE bound based on spectral complexity for deep convolutional neural networks and provide tighter bounds by orders of magnitude from the previous estimate. We then investigate theoretically and empirically the insensitivity of spectral complexity to invariances of modern deep convolutional neural networks, and show several limitations of spectral complexity that occur as a result.

Revisiting hard thresholding for DNN pruning

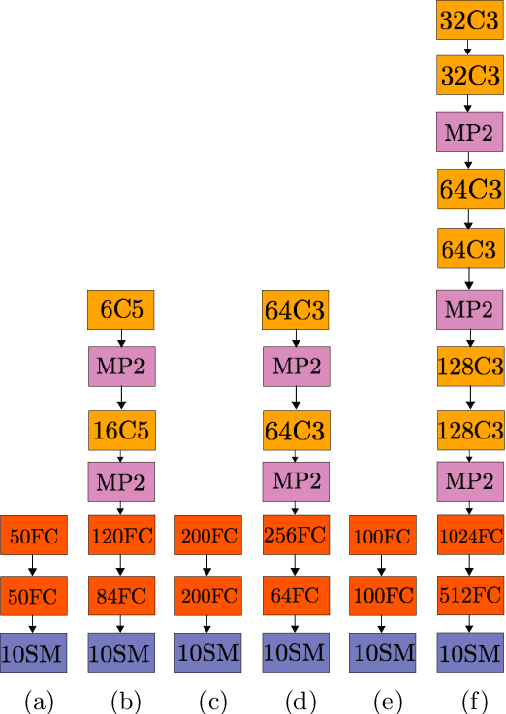
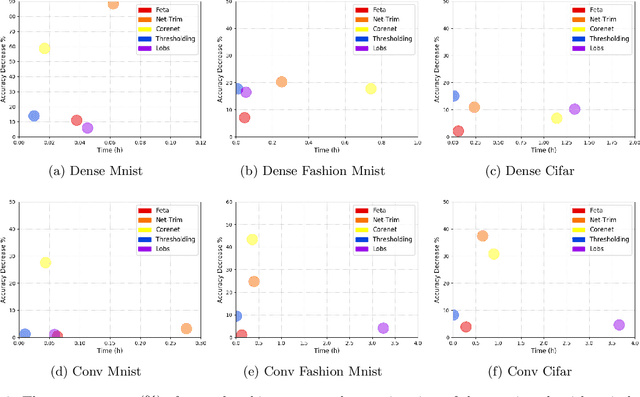
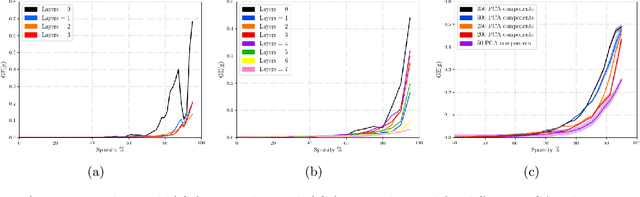
The most common method for DNN pruning is hard thresholding of network weights, followed by retraining to recover any lost accuracy. Recently developed smart pruning algorithms use the DNN response over the training set for a variety of cost functions to determine redundant network weights, leading to less accuracy degradation and possibly less retraining time. For experiments on the total pruning time (pruning time + retraining time) we show that hard thresholding followed by retraining remains the most efficient way of reducing the number of network parameters. However smart pruning algorithms still have advantages when retraining is not possible. In this context we propose a novel smart pruning algorithm based on difference of convex functions optimisation and show that it is often orders of magnitude faster than competing approaches while achieving the lowest classification accuracy degradation. Furthermore we investigate theoretically the effect of hard thresholding on DNN accuracy. We show that accuracy degradation increases with remaining network depth from the pruned layer. We also discover a link between the latent dimensionality of the training data manifold and network robustness to hard thresholding.