Implicit Gaussian process representation of vector fields over arbitrary latent manifolds

Gaussian processes (GPs) are popular nonparametric statistical models for learning unknown functions and quantifying the spatiotemporal uncertainty in data. Recent works have extended GPs to model scalar and vector quantities distributed over non-Euclidean domains, including smooth manifolds appearing in numerous fields such as computer vision, dynamical systems, and neuroscience. However, these approaches assume that the manifold underlying the data is known, limiting their practical utility. We introduce RVGP, a generalisation of GPs for learning vector signals over latent Riemannian manifolds. Our method uses positional encoding with eigenfunctions of the connection Laplacian, associated with the tangent bundle, readily derived from common graph-based approximation of data. We demonstrate that RVGP possesses global regularity over the manifold, which allows it to super-resolve and inpaint vector fields while preserving singularities. Furthermore, we use RVGP to reconstruct high-density neural dynamics derived from low-density EEG recordings in healthy individuals and Alzheimer's patients. We show that vector field singularities are important disease markers and that their reconstruction leads to a comparable classification accuracy of disease states to high-density recordings. Thus, our method overcomes a significant practical limitation in experimental and clinical applications.

Interpretable statistical representations of neural population dynamics and geometry

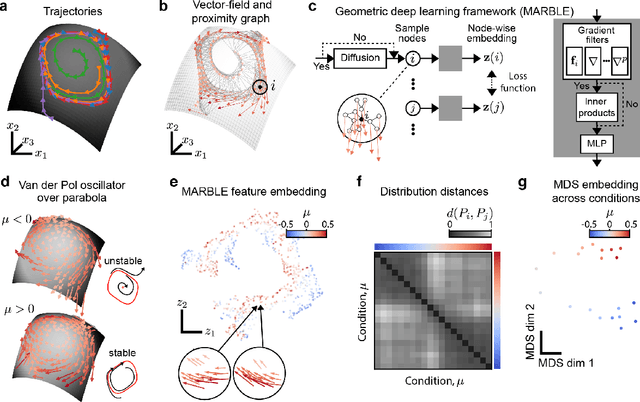
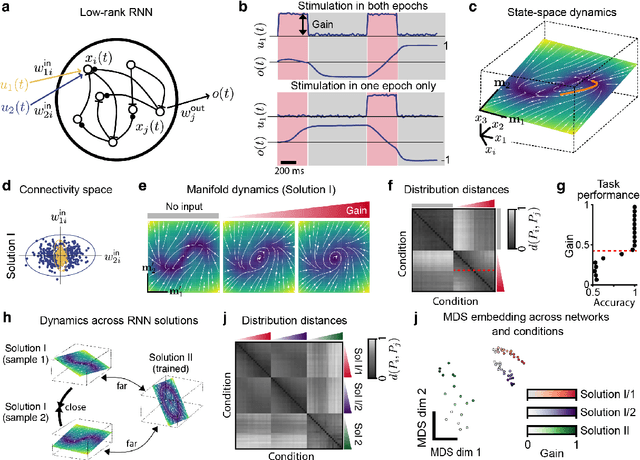
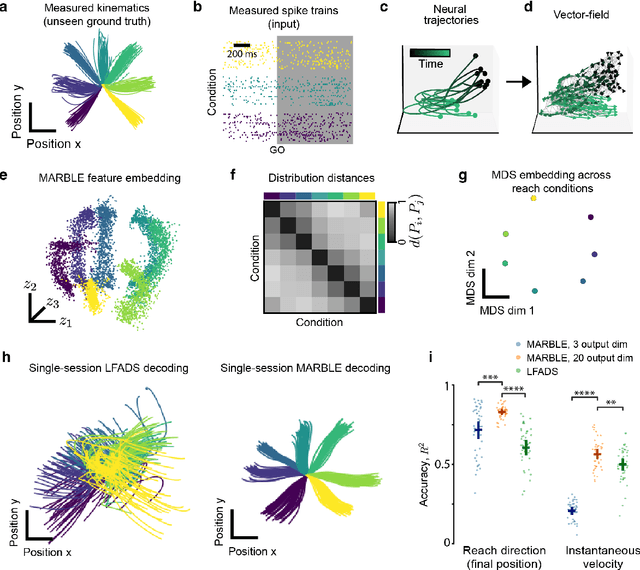
The dynamics of neuron populations during diverse tasks often evolve on low-dimensional manifolds. However, it remains challenging to discern the contributions of geometry and dynamics for encoding relevant behavioural variables. Here, we introduce an unsupervised geometric deep learning framework for representing non-linear dynamical systems based on statistical distributions of local phase portrait features. Our method provides robust geometry-aware or geometry-agnostic representations for the unbiased comparison of dynamics based on measured trajectories. We demonstrate that our statistical representation can generalise across neural network instances to discriminate computational mechanisms, obtain interpretable embeddings of neural dynamics in a primate reaching task with geometric correspondence to hand kinematics, and develop a decoding algorithm with state-of-the-art accuracy. Our results highlight the importance of using the intrinsic manifold structure over temporal information to develop better decoding algorithms and assimilate data across experiments.

Generalised Implicit Neural Representations

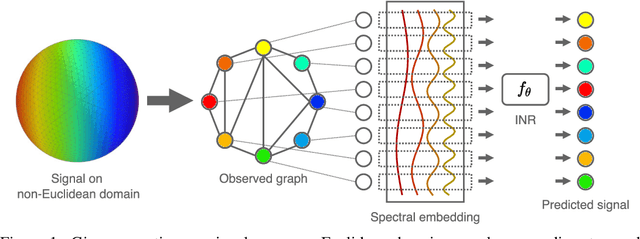
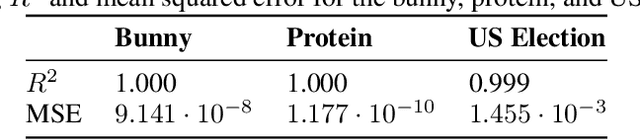
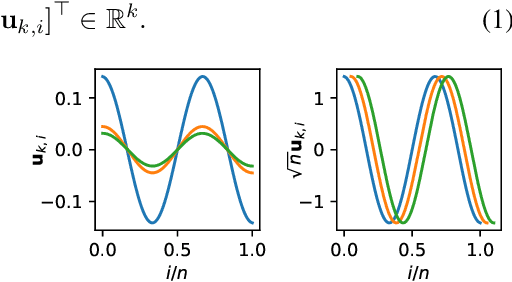
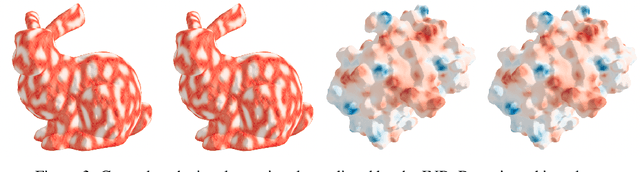
We consider the problem of learning implicit neural representations (INRs) for signals on non-Euclidean domains. In the Euclidean case, INRs are trained on a discrete sampling of a signal over a regular lattice. Here, we assume that the continuous signal exists on some unknown topological space from which we sample a discrete graph. In the absence of a coordinate system to identify the sampled nodes, we propose approximating their location with a spectral embedding of the graph. This allows us to train INRs without knowing the underlying continuous domain, which is the case for most graph signals in nature, while also making the INRs equivariant under the symmetry group of the domain. We show experiments with our method on various real-world signals on non-Euclidean domains.

Some limitations of norm based generalization bounds in deep neural networks

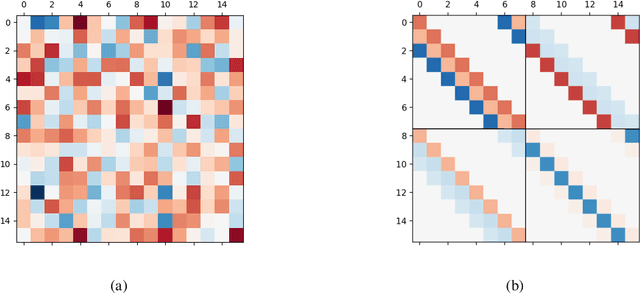
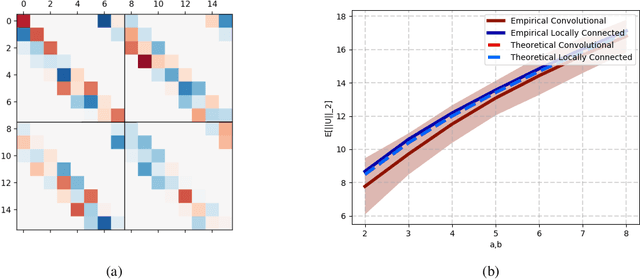
Deep convolutional neural networks have been shown to be able to fit a labeling over random data while still being able to generalize well on normal datasets. Describing deep convolutional neural network capacity through the measure of spectral complexity has been recently proposed to tackle this apparent paradox. Spectral complexity correlates with GE and can distinguish networks trained on normal and random labels. We propose the first GE bound based on spectral complexity for deep convolutional neural networks and provide tighter bounds by orders of magnitude from the previous estimate. We then investigate theoretically and empirically the insensitivity of spectral complexity to invariances of modern deep convolutional neural networks, and show several limitations of spectral complexity that occur as a result.

Revisiting hard thresholding for DNN pruning

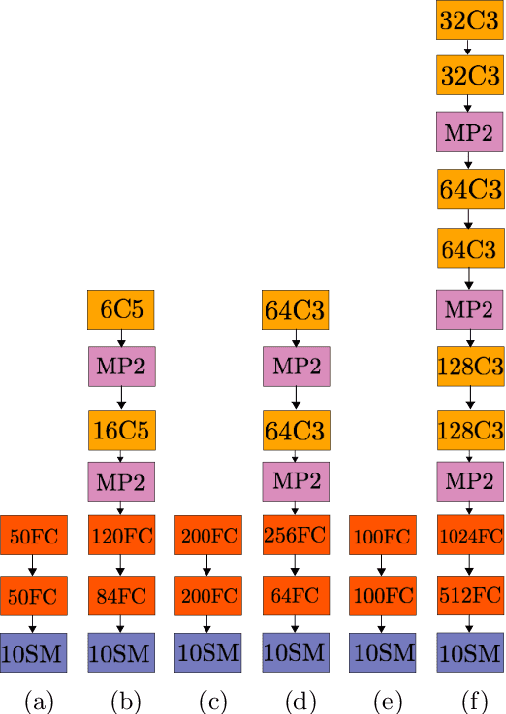
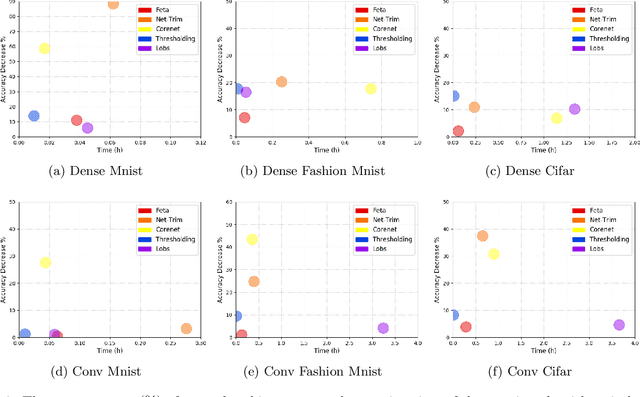
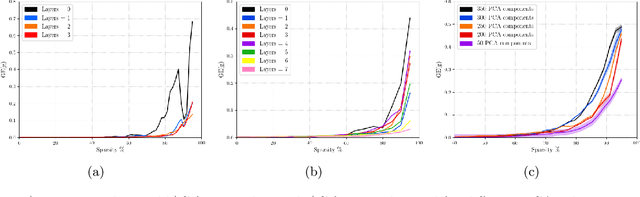
The most common method for DNN pruning is hard thresholding of network weights, followed by retraining to recover any lost accuracy. Recently developed smart pruning algorithms use the DNN response over the training set for a variety of cost functions to determine redundant network weights, leading to less accuracy degradation and possibly less retraining time. For experiments on the total pruning time (pruning time + retraining time) we show that hard thresholding followed by retraining remains the most efficient way of reducing the number of network parameters. However smart pruning algorithms still have advantages when retraining is not possible. In this context we propose a novel smart pruning algorithm based on difference of convex functions optimisation and show that it is often orders of magnitude faster than competing approaches while achieving the lowest classification accuracy degradation. Furthermore we investigate theoretically the effect of hard thresholding on DNN accuracy. We show that accuracy degradation increases with remaining network depth from the pruned layer. We also discover a link between the latent dimensionality of the training data manifold and network robustness to hard thresholding.

A Graph-structured Dataset for Wikipedia Research

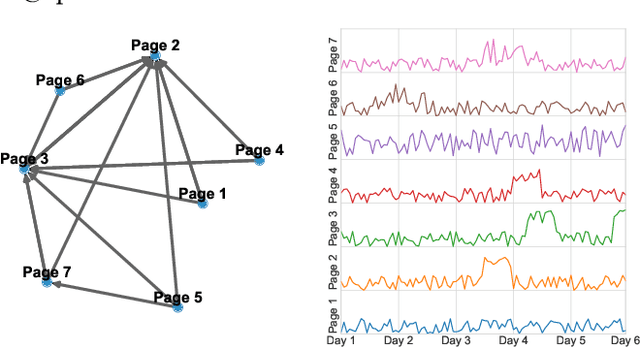
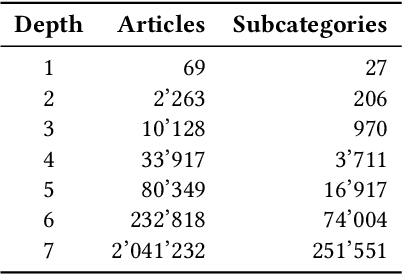
Wikipedia is a rich and invaluable source of information. Its central place on the Web makes it a particularly interesting object of study for scientists. Researchers from different domains used various complex datasets related to Wikipedia to study language, social behavior, knowledge organization, and network theory. While being a scientific treasure, the large size of the dataset hinders pre-processing and may be a challenging obstacle for potential new studies. This issue is particularly acute in scientific domains where researchers may not be technically and data processing savvy. On one hand, the size of Wikipedia dumps is large. It makes the parsing and extraction of relevant information cumbersome. On the other hand, the API is straightforward to use but restricted to a relatively small number of requests. The middle ground is at the mesoscopic scale when researchers need a subset of Wikipedia ranging from thousands to hundreds of thousands of pages but there exists no efficient solution at this scale. In this work, we propose an efficient data structure to make requests and access subnetworks of Wikipedia pages and categories. We provide convenient tools for accessing and filtering viewership statistics or "pagecounts" of Wikipedia web pages. The dataset organization leverages principles of graph databases that allows rapid and intuitive access to subgraphs of Wikipedia articles and categories. The dataset and deployment guidelines are available on the LTS2 website \url{https://lts2.epfl.ch/Datasets/Wikipedia/}.

Anomaly detection in the dynamics of web and social networks

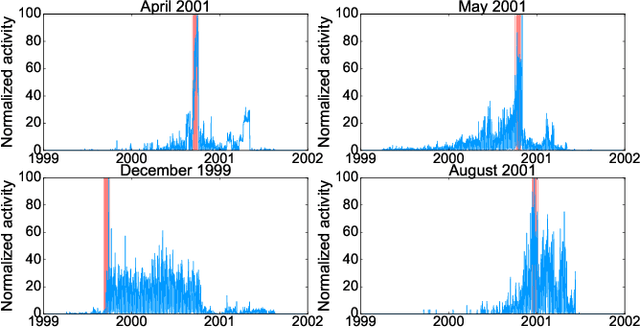
In this work, we propose a new, fast and scalable method for anomaly detection in large time-evolving graphs. It may be a static graph with dynamic node attributes (e.g. time-series), or a graph evolving in time, such as a temporal network. We define an anomaly as a localized increase in temporal activity in a cluster of nodes. The algorithm is unsupervised. It is able to detect and track anomalous activity in a dynamic network despite the noise from multiple interfering sources. We use the Hopfield network model of memory to combine the graph and time information. We show that anomalies can be spotted with a good precision using a memory network. The presented approach is scalable and we provide a distributed implementation of the algorithm. To demonstrate its efficiency, we apply it to two datasets: Enron Email dataset and Wikipedia page views. We show that the anomalous spikes are triggered by the real-world events that impact the network dynamics. Besides, the structure of the clusters and the analysis of the time evolution associated with the detected events reveals interesting facts on how humans interact, exchange and search for information, opening the door to new quantitative studies on collective and social behavior on large and dynamic datasets.

Geodesic convolutional neural networks on Riemannian manifolds

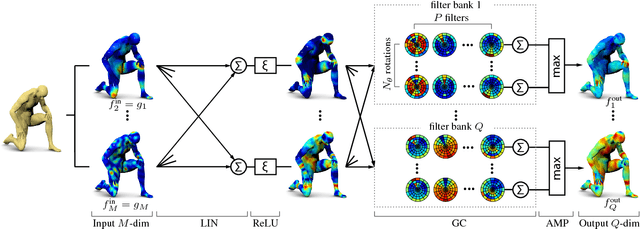
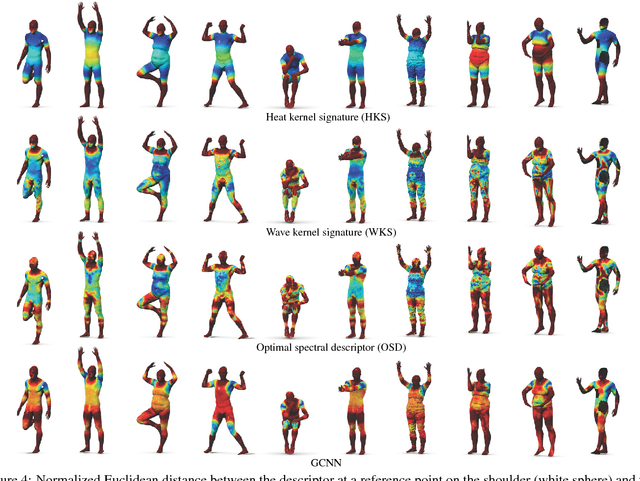
Feature descriptors play a crucial role in a wide range of geometry analysis and processing applications, including shape correspondence, retrieval, and segmentation. In this paper, we introduce Geodesic Convolutional Neural Networks (GCNN), a generalization of the convolutional networks (CNN) paradigm to non-Euclidean manifolds. Our construction is based on a local geodesic system of polar coordinates to extract "patches", which are then passed through a cascade of filters and linear and non-linear operators. The coefficients of the filters and linear combination weights are optimization variables that are learned to minimize a task-specific cost function. We use GCNN to learn invariant shape features, allowing to achieve state-of-the-art performance in problems such as shape description, retrieval, and correspondence.

PAC-Bayesian Margin Bounds for Convolutional Neural Networks

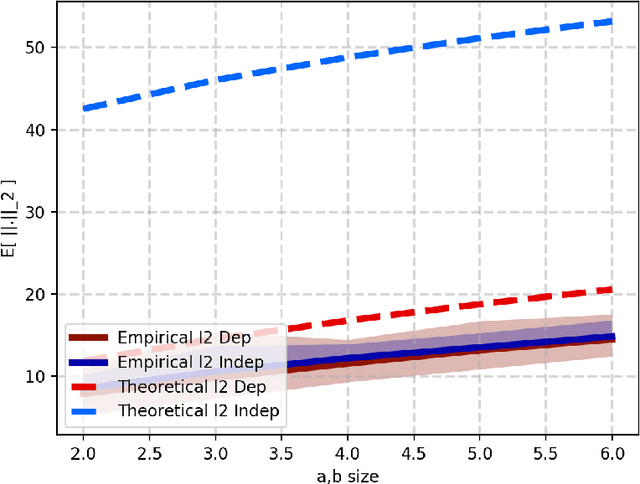
Recently the generalization error of deep neural networks has been analyzed through the PAC-Bayesian framework, for the case of fully connected layers. We adapt this approach to the convolutional setting.

Adaptive Graph-based Total Variation for Tomographic Reconstructions

Sparsity exploiting image reconstruction (SER) methods have been extensively used with Total Variation (TV) regularization for tomographic reconstructions. Local TV methods fail to preserve texture details and often create additional artefacts due to over-smoothing. Non-Local TV (NLTV) methods have been proposed as a solution to this but they either lack continuous updates due to computational constraints or limit the locality to a small region. In this paper, we propose Adaptive Graph-based TV (AGTV). The proposed method goes beyond spatial similarity between different regions of an image being reconstructed by establishing a connection between similar regions in the entire image regardless of spatial distance. As compared to NLTV the proposed method is computationally efficient and involves updating the graph prior during every iteration making the connection between similar regions stronger. Moreover, it promotes sparsity in the wavelet and graph gradient domains. Since TV is a special case of graph TV the proposed method can also be seen as a generalization of SER and TV methods.