Fast accuracy estimation of deep learning based multi-class musical source separation

Music source separation represents the task of extracting all the instruments from a given song. Recent breakthroughs on this challenge have gravitated around a single dataset, MUSDB, that is limited to four instrument classes only. New datasets are required to extend to other instruments and increase the performances. However larger datasets are costly and time-consuming in terms of collecting data and training deep networks. In this work, we propose a fast method for evaluating the separability of instruments in any dataset or song, and for any instrument without the need to train and tune a deep neural network. This separability measure helps selecting appropriate samples for the efficient training of neural networks. Our approach, based on the oracle principle with an ideal ratio mask, is a good proxy to estimate the separation performances of state-of-the-art deep learning approaches based on time-frequency masking such as TasNet or Open-Unmix. The proposed fast accuracy estimation method can significantly speed up the music source separation system's development process.

A Graph-structured Dataset for Wikipedia Research

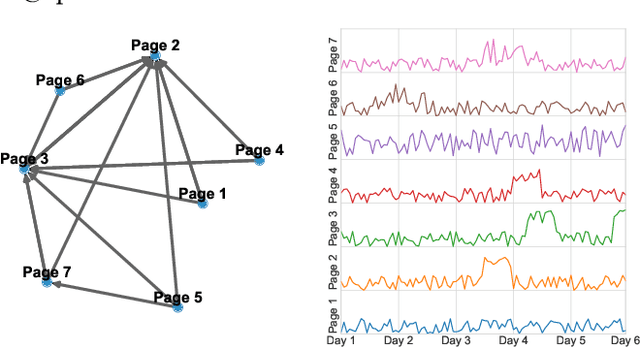
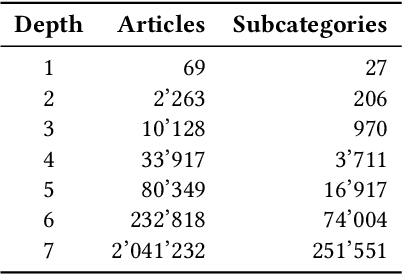
Wikipedia is a rich and invaluable source of information. Its central place on the Web makes it a particularly interesting object of study for scientists. Researchers from different domains used various complex datasets related to Wikipedia to study language, social behavior, knowledge organization, and network theory. While being a scientific treasure, the large size of the dataset hinders pre-processing and may be a challenging obstacle for potential new studies. This issue is particularly acute in scientific domains where researchers may not be technically and data processing savvy. On one hand, the size of Wikipedia dumps is large. It makes the parsing and extraction of relevant information cumbersome. On the other hand, the API is straightforward to use but restricted to a relatively small number of requests. The middle ground is at the mesoscopic scale when researchers need a subset of Wikipedia ranging from thousands to hundreds of thousands of pages but there exists no efficient solution at this scale. In this work, we propose an efficient data structure to make requests and access subnetworks of Wikipedia pages and categories. We provide convenient tools for accessing and filtering viewership statistics or "pagecounts" of Wikipedia web pages. The dataset organization leverages principles of graph databases that allows rapid and intuitive access to subgraphs of Wikipedia articles and categories. The dataset and deployment guidelines are available on the LTS2 website \url{https://lts2.epfl.ch/Datasets/Wikipedia/}.

Anomaly detection in the dynamics of web and social networks

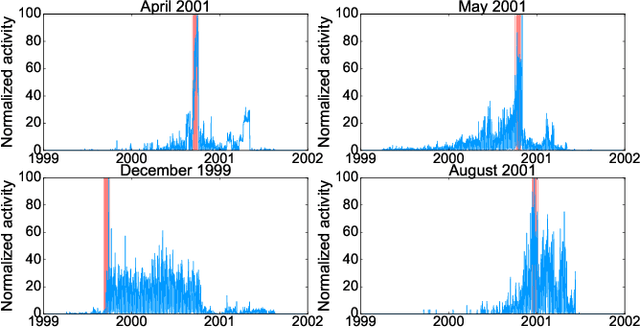
In this work, we propose a new, fast and scalable method for anomaly detection in large time-evolving graphs. It may be a static graph with dynamic node attributes (e.g. time-series), or a graph evolving in time, such as a temporal network. We define an anomaly as a localized increase in temporal activity in a cluster of nodes. The algorithm is unsupervised. It is able to detect and track anomalous activity in a dynamic network despite the noise from multiple interfering sources. We use the Hopfield network model of memory to combine the graph and time information. We show that anomalies can be spotted with a good precision using a memory network. The presented approach is scalable and we provide a distributed implementation of the algorithm. To demonstrate its efficiency, we apply it to two datasets: Enron Email dataset and Wikipedia page views. We show that the anomalous spikes are triggered by the real-world events that impact the network dynamics. Besides, the structure of the clusters and the analysis of the time evolution associated with the detected events reveals interesting facts on how humans interact, exchange and search for information, opening the door to new quantitative studies on collective and social behavior on large and dynamic datasets.

A Time-Vertex Signal Processing Framework

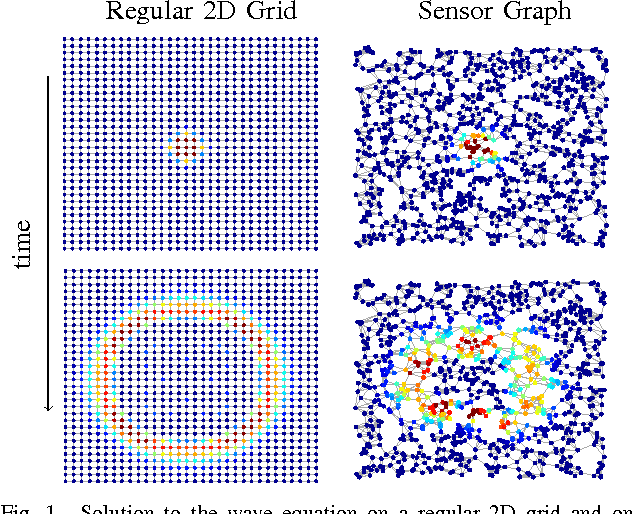
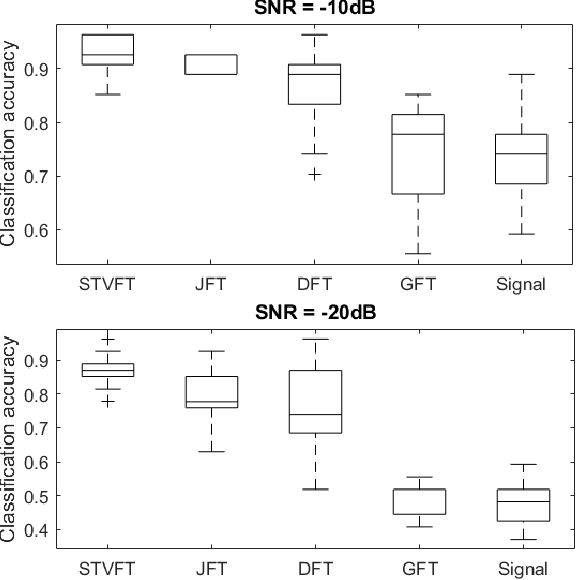
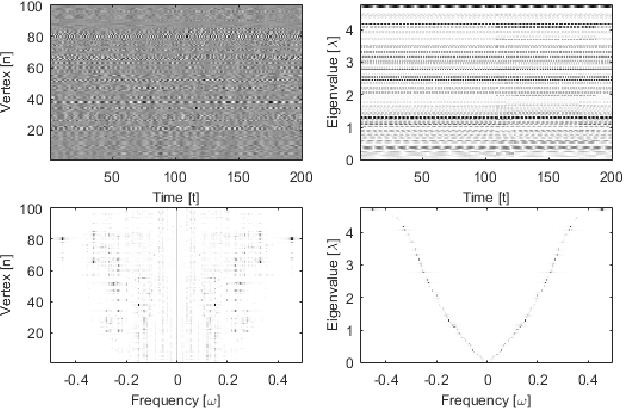
An emerging way to deal with high-dimensional non-euclidean data is to assume that the underlying structure can be captured by a graph. Recently, ideas have begun to emerge related to the analysis of time-varying graph signals. This work aims to elevate the notion of joint harmonic analysis to a full-fledged framework denoted as Time-Vertex Signal Processing, that links together the time-domain signal processing techniques with the new tools of graph signal processing. This entails three main contributions: (a) We provide a formal motivation for harmonic time-vertex analysis as an analysis tool for the state evolution of simple Partial Differential Equations on graphs. (b) We improve the accuracy of joint filtering operators by up-to two orders of magnitude. (c) Using our joint filters, we construct time-vertex dictionaries analyzing the different scales and the local time-frequency content of a signal. The utility of our tools is illustrated in numerous applications and datasets, such as dynamic mesh denoising and classification, still-video inpainting, and source localization in seismic events. Our results suggest that joint analysis of time-vertex signals can bring benefits to regression and learning.

Tracking Time-Vertex Propagation using Dynamic Graph Wavelets

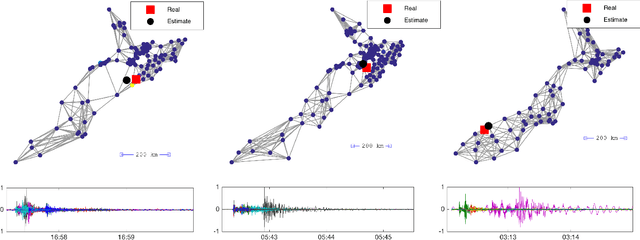
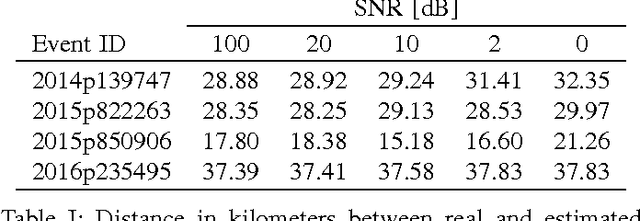
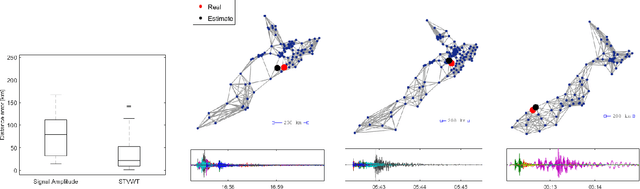
Graph Signal Processing generalizes classical signal processing to signal or data indexed by the vertices of a weighted graph. So far, the research efforts have been focused on static graph signals. However numerous applications involve graph signals evolving in time, such as spreading or propagation of waves on a network. The analysis of this type of data requires a new set of methods that fully takes into account the time and graph dimensions. We propose a novel class of wavelet frames named Dynamic Graph Wavelets, whose time-vertex evolution follows a dynamic process. We demonstrate that this set of functions can be combined with sparsity based approaches such as compressive sensing to reveal information on the dynamic processes occurring on a graph. Experiments on real seismological data show the efficiency of the technique, allowing to estimate the epicenter of earthquake events recorded by a seismic network.

Global and Local Uncertainty Principles for Signals on Graphs

Uncertainty principles such as Heisenberg's provide limits on the time-frequency concentration of a signal, and constitute an important theoretical tool for designing and evaluating linear signal transforms. Generalizations of such principles to the graph setting can inform dictionary design for graph signals, lead to algorithms for reconstructing missing information from graph signals via sparse representations, and yield new graph analysis tools. While previous work has focused on generalizing notions of spreads of a graph signal in the vertex and graph spectral domains, our approach is to generalize the methods of Lieb in order to develop uncertainty principles that provide limits on the concentration of the analysis coefficients of any graph signal under a dictionary transform whose atoms are jointly localized in the vertex and graph spectral domains. One challenge we highlight is that due to the inhomogeneity of the underlying graph data domain, the local structure in a single small region of the graph can drastically affect the uncertainty bounds for signals concentrated in different regions of the graph, limiting the information provided by global uncertainty principles. Accordingly, we suggest a new way to incorporate a notion of locality, and develop local uncertainty principles that bound the concentration of the analysis coefficients of each atom of a localized graph spectral filter frame in terms of quantities that depend on the local structure of the graph around the center vertex of the given atom. Finally, we demonstrate how our proposed local uncertainty measures can improve the random sampling of graph signals.