On the Sum of Random Samples with Bounded Pareto Distribution

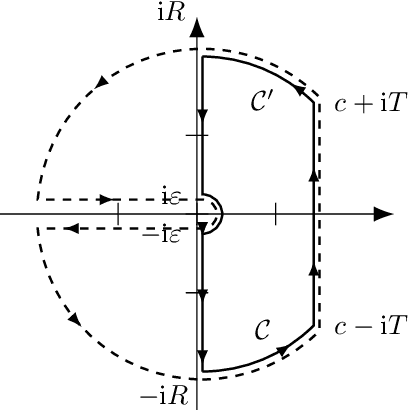
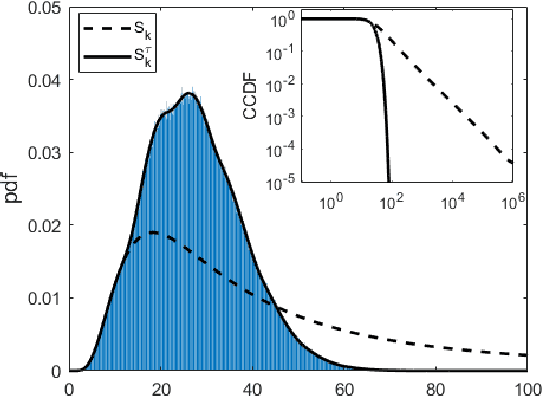
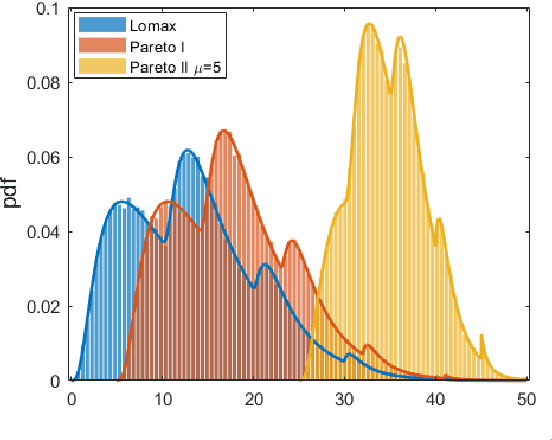
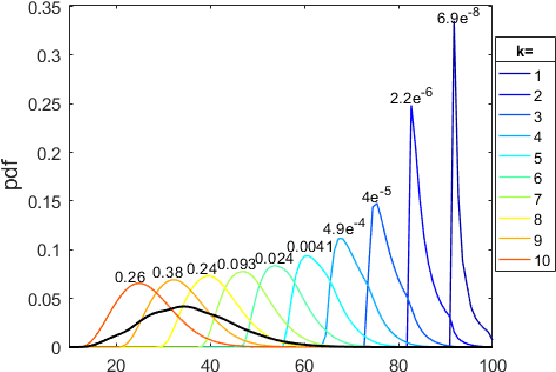
Heavy-tailed random samples, as well as their sum or average, are encountered in a number of signal processing applications in radar, communications, finance, and natural sciences. Modeling such data through the Pareto distribution is particularly attractive due to its simple analytical form, but may lead to infinite variance and/or mean, which is not physically plausible: in fact, samples are always bounded in practice, namely because of clipping during the signal acquisition or deliberate censoring or trimming (truncation) at the processing stage. Based on this motivation, the paper derives and analyzes the distribution of the sum of right-censored Pareto Type-II variables, which generalizes the conventional Pareto (Type-I) and Lomax distributions. The distribution of the sum of truncated Pareto is also obtained, and an analytical connection is drawn with the unbounded case. A numerical analysis illustrates the findings, providing insights on several aspects including the intimate mixture structure of the obtained expressions.

Resource Aware Multifidelity Active Learning for Efficient Optimization

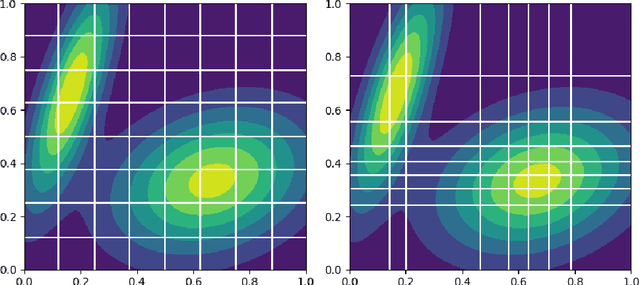
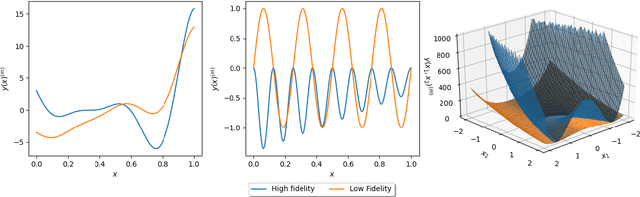
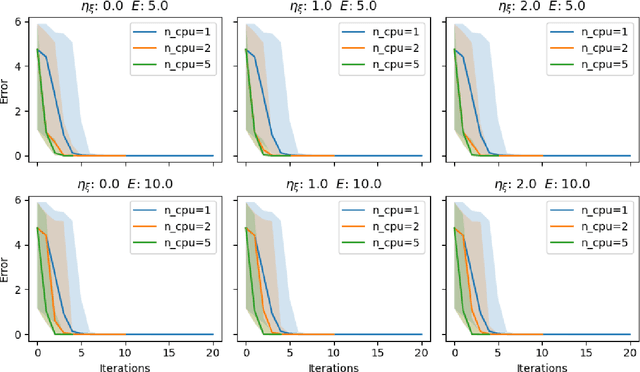
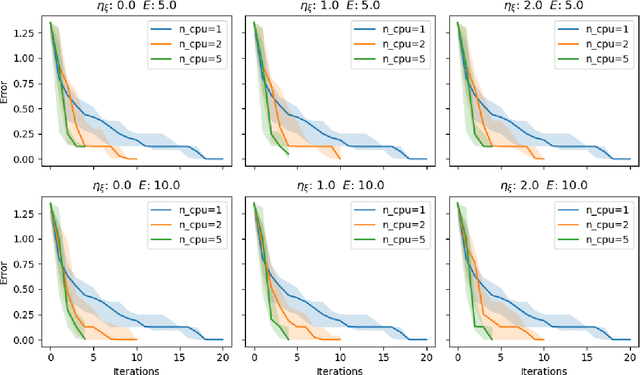
Traditional methods for black box optimization require a considerable number of evaluations which can be time consuming, unpractical, and often unfeasible for many engineering applications that rely on accurate representations and expensive models to evaluate. Bayesian Optimization (BO) methods search for the global optimum by progressively (actively) learning a surrogate model of the objective function along the search path. Bayesian optimization can be accelerated through multifidelity approaches which leverage multiple black-box approximations of the objective functions that can be computationally cheaper to evaluate, but still provide relevant information to the search task. Further computational benefits are offered by the availability of parallel and distributed computing architectures whose optimal usage is an open opportunity within the context of active learning. This paper introduces the Resource Aware Active Learning (RAAL) strategy, a multifidelity Bayesian scheme to accelerate the optimization of black box functions. At each optimization step, the RAAL procedure computes the set of best sample locations and the associated fidelity sources that maximize the information gain to acquire during the parallel/distributed evaluation of the objective function, while accounting for the limited computational budget. The scheme is demonstrated for a variety of benchmark problems and results are discussed for both single fidelity and multifidelity settings. In particular we observe that the RAAL strategy optimally seeds multiple points at each iteration allowing for a major speed up of the optimization task.

A Time-Vertex Signal Processing Framework

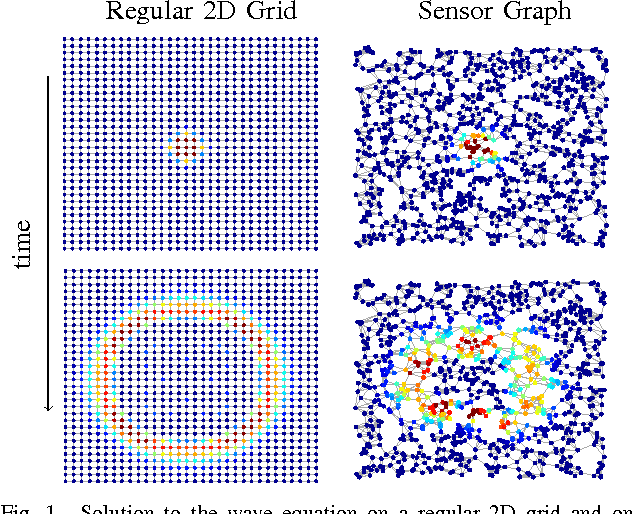
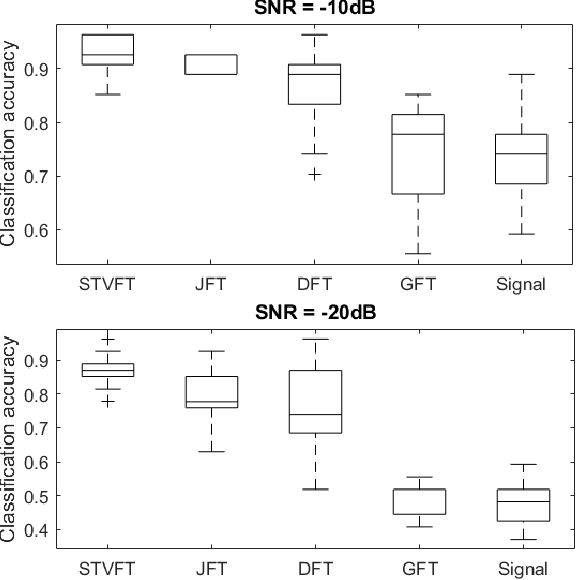
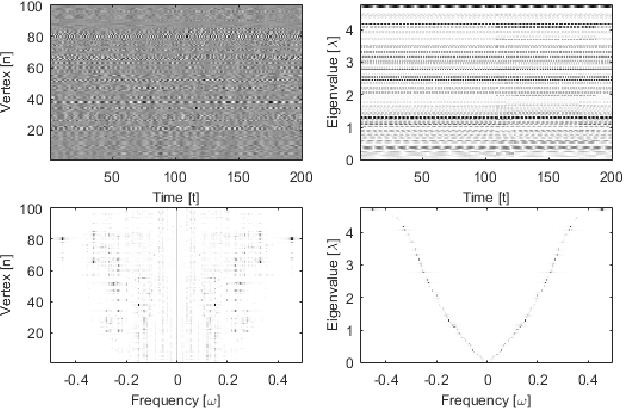
An emerging way to deal with high-dimensional non-euclidean data is to assume that the underlying structure can be captured by a graph. Recently, ideas have begun to emerge related to the analysis of time-varying graph signals. This work aims to elevate the notion of joint harmonic analysis to a full-fledged framework denoted as Time-Vertex Signal Processing, that links together the time-domain signal processing techniques with the new tools of graph signal processing. This entails three main contributions: (a) We provide a formal motivation for harmonic time-vertex analysis as an analysis tool for the state evolution of simple Partial Differential Equations on graphs. (b) We improve the accuracy of joint filtering operators by up-to two orders of magnitude. (c) Using our joint filters, we construct time-vertex dictionaries analyzing the different scales and the local time-frequency content of a signal. The utility of our tools is illustrated in numerous applications and datasets, such as dynamic mesh denoising and classification, still-video inpainting, and source localization in seismic events. Our results suggest that joint analysis of time-vertex signals can bring benefits to regression and learning.

Multilinear Low-Rank Tensors on Graphs & Applications

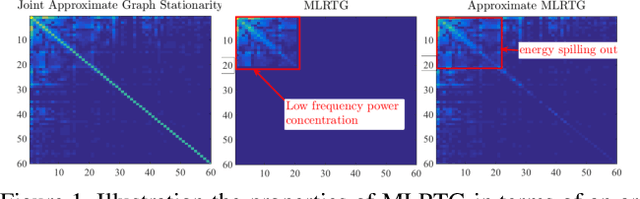
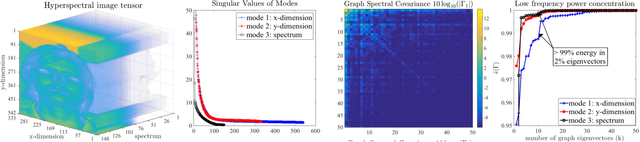
We propose a new framework for the analysis of low-rank tensors which lies at the intersection of spectral graph theory and signal processing. As a first step, we present a new graph based low-rank decomposition which approximates the classical low-rank SVD for matrices and multi-linear SVD for tensors. Then, building on this novel decomposition we construct a general class of convex optimization problems for approximately solving low-rank tensor inverse problems, such as tensor Robust PCA. The whole framework is named as 'Multilinear Low-rank tensors on Graphs (MLRTG)'. Our theoretical analysis shows: 1) MLRTG stands on the notion of approximate stationarity of multi-dimensional signals on graphs and 2) the approximation error depends on the eigen gaps of the graphs. We demonstrate applications for a wide variety of 4 artificial and 12 real tensor datasets, such as EEG, FMRI, BCI, surveillance videos and hyperspectral images. Generalization of the tensor concepts to non-euclidean domain, orders of magnitude speed-up, low-memory requirement and significantly enhanced performance at low SNR are the key aspects of our framework.

Towards stationary time-vertex signal processing

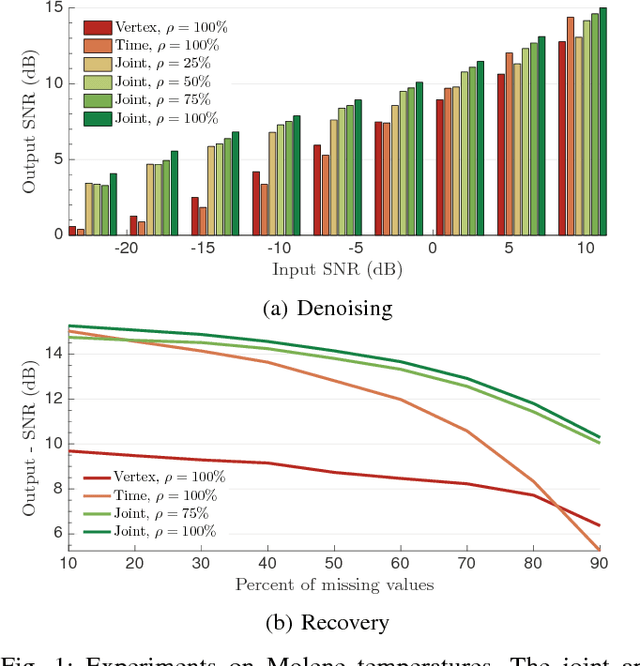
Graph-based methods for signal processing have shown promise for the analysis of data exhibiting irregular structure, such as those found in social, transportation, and sensor networks. Yet, though these systems are often dynamic, state-of-the-art methods for signal processing on graphs ignore the dimension of time, treating successive graph signals independently or taking a global average. To address this shortcoming, this paper considers the statistical analysis of time-varying graph signals. We introduce a novel definition of joint (time-vertex) stationarity, which generalizes the classical definition of time stationarity and the more recent definition appropriate for graphs. Joint stationarity gives rise to a scalable Wiener optimization framework for joint denoising, semi-supervised learning, or more generally inversing a linear operator, that is provably optimal. Experimental results on real weather data demonstrate that taking into account graph and time dimensions jointly can yield significant accuracy improvements in the reconstruction effort.

Tracking Time-Vertex Propagation using Dynamic Graph Wavelets

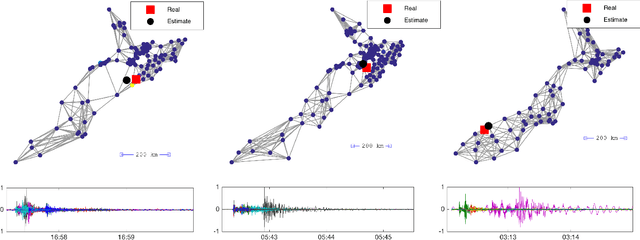
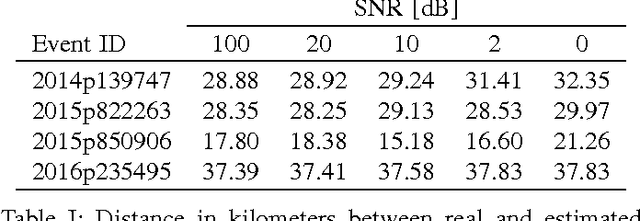
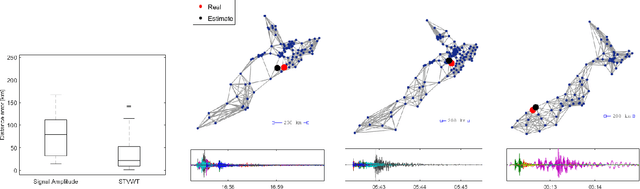
Graph Signal Processing generalizes classical signal processing to signal or data indexed by the vertices of a weighted graph. So far, the research efforts have been focused on static graph signals. However numerous applications involve graph signals evolving in time, such as spreading or propagation of waves on a network. The analysis of this type of data requires a new set of methods that fully takes into account the time and graph dimensions. We propose a novel class of wavelet frames named Dynamic Graph Wavelets, whose time-vertex evolution follows a dynamic process. We demonstrate that this set of functions can be combined with sparsity based approaches such as compressive sensing to reveal information on the dynamic processes occurring on a graph. Experiments on real seismological data show the efficiency of the technique, allowing to estimate the epicenter of earthquake events recorded by a seismic network.