On the Sum of Random Samples with Bounded Pareto Distribution
Paper and Code
May 03, 2021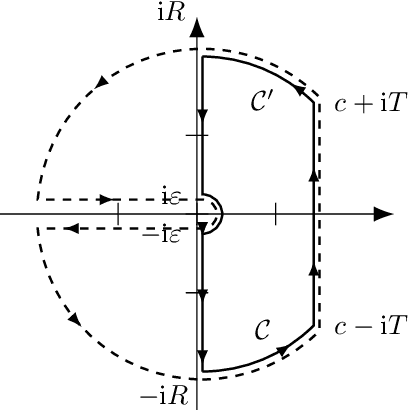
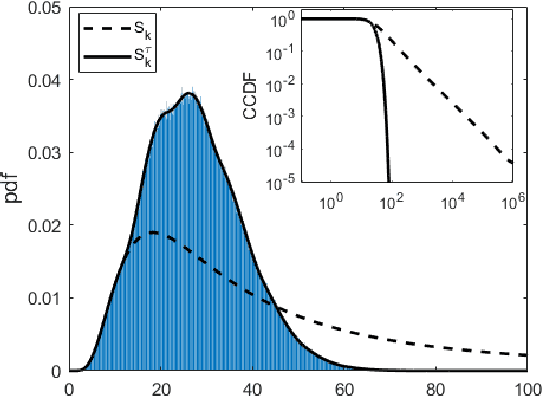
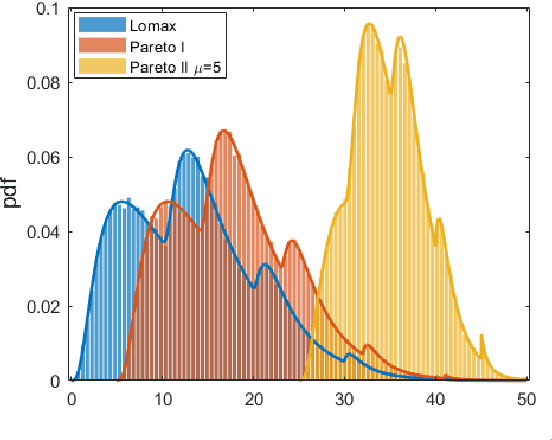
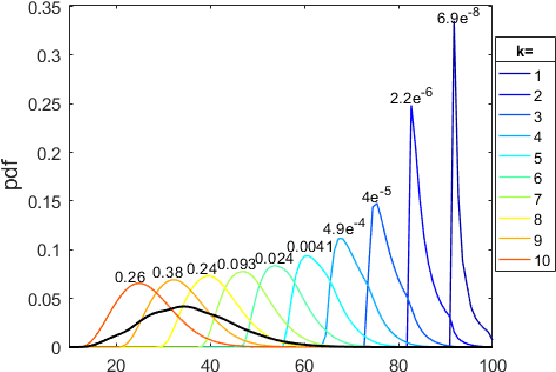
Heavy-tailed random samples, as well as their sum or average, are encountered in a number of signal processing applications in radar, communications, finance, and natural sciences. Modeling such data through the Pareto distribution is particularly attractive due to its simple analytical form, but may lead to infinite variance and/or mean, which is not physically plausible: in fact, samples are always bounded in practice, namely because of clipping during the signal acquisition or deliberate censoring or trimming (truncation) at the processing stage. Based on this motivation, the paper derives and analyzes the distribution of the sum of right-censored Pareto Type-II variables, which generalizes the conventional Pareto (Type-I) and Lomax distributions. The distribution of the sum of truncated Pareto is also obtained, and an analytical connection is drawn with the unbounded case. A numerical analysis illustrates the findings, providing insights on several aspects including the intimate mixture structure of the obtained expressions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge