Policy Gradient with Active Importance Sampling

Importance sampling (IS) represents a fundamental technique for a large surge of off-policy reinforcement learning approaches. Policy gradient (PG) methods, in particular, significantly benefit from IS, enabling the effective reuse of previously collected samples, thus increasing sample efficiency. However, classically, IS is employed in RL as a passive tool for re-weighting historical samples. However, the statistical community employs IS as an active tool combined with the use of behavioral distributions that allow the reduction of the estimate variance even below the sample mean one. In this paper, we focus on this second setting by addressing the behavioral policy optimization (BPO) problem. We look for the best behavioral policy from which to collect samples to reduce the policy gradient variance as much as possible. We provide an iterative algorithm that alternates between the cross-entropy estimation of the minimum-variance behavioral policy and the actual policy optimization, leveraging on defensive IS. We theoretically analyze such an algorithm, showing that it enjoys a convergence rate of order $O(\epsilon^{-4})$ to a stationary point, but depending on a more convenient variance term w.r.t. standard PG methods. We then provide a practical version that is numerically validated, showing the advantages in the policy gradient estimation variance and on the learning speed.

Resource Aware Multifidelity Active Learning for Efficient Optimization

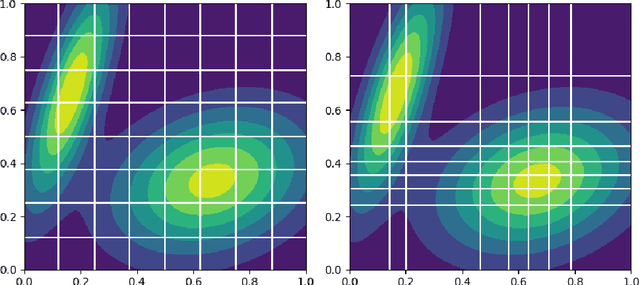
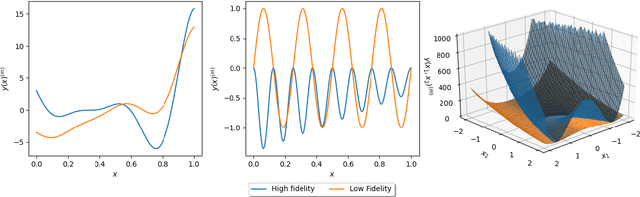
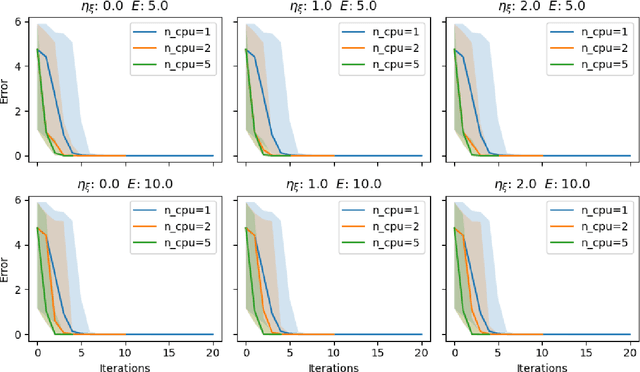
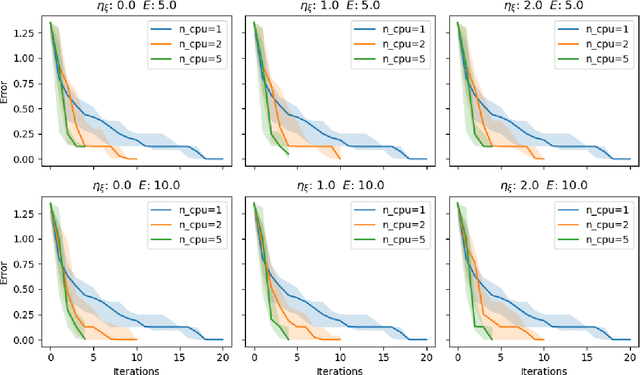
Traditional methods for black box optimization require a considerable number of evaluations which can be time consuming, unpractical, and often unfeasible for many engineering applications that rely on accurate representations and expensive models to evaluate. Bayesian Optimization (BO) methods search for the global optimum by progressively (actively) learning a surrogate model of the objective function along the search path. Bayesian optimization can be accelerated through multifidelity approaches which leverage multiple black-box approximations of the objective functions that can be computationally cheaper to evaluate, but still provide relevant information to the search task. Further computational benefits are offered by the availability of parallel and distributed computing architectures whose optimal usage is an open opportunity within the context of active learning. This paper introduces the Resource Aware Active Learning (RAAL) strategy, a multifidelity Bayesian scheme to accelerate the optimization of black box functions. At each optimization step, the RAAL procedure computes the set of best sample locations and the associated fidelity sources that maximize the information gain to acquire during the parallel/distributed evaluation of the objective function, while accounting for the limited computational budget. The scheme is demonstrated for a variety of benchmark problems and results are discussed for both single fidelity and multifidelity settings. In particular we observe that the RAAL strategy optimally seeds multiple points at each iteration allowing for a major speed up of the optimization task.