Reusing Trajectories in Policy Gradients Enables Fast Convergence

Policy gradient (PG) methods are a class of effective reinforcement learning algorithms, particularly when dealing with continuous control problems. These methods learn the parameters of parametric policies via stochastic gradient ascent, typically using on-policy trajectory data to estimate the policy gradient. However, such reliance on fresh data makes them sample-inefficient. Indeed, vanilla PG methods require $O(\epsilon^{-2})$ trajectories to reach an $\epsilon$-approximate stationary point. A common strategy to improve efficiency is to reuse off-policy information from past iterations, such as previous gradients or trajectories. While gradient reuse has received substantial theoretical attention, leading to improved rates of $O(\epsilon^{-3/2})$, the reuse of past trajectories remains largely unexplored from a theoretical perspective. In this work, we provide the first rigorous theoretical evidence that extensive reuse of past off-policy trajectories can significantly accelerate convergence in PG methods. We introduce a power mean correction to the multiple importance weighting estimator and propose RPG (Retrospective Policy Gradient), a PG algorithm that combines old and new trajectories for policy updates. Through a novel analysis, we show that, under established assumptions, RPG achieves a sample complexity of $\widetilde{O}(\epsilon^{-1})$, the best known rate in the literature. We further validate empirically our approach against PG methods with state-of-the-art rates.

Learning Deterministic Policies with Policy Gradients in Constrained Markov Decision Processes

Constrained Reinforcement Learning (CRL) addresses sequential decision-making problems where agents are required to achieve goals by maximizing the expected return while meeting domain-specific constraints. In this setting, policy-based methods are widely used thanks to their advantages when dealing with continuous-control problems. These methods search in the policy space with an action-based or a parameter-based exploration strategy, depending on whether they learn the parameters of a stochastic policy or those of a stochastic hyperpolicy. We introduce an exploration-agnostic algorithm, called C-PG, which enjoys global last-iterate convergence guarantees under gradient domination assumptions. Furthermore, under specific noise models where the (hyper)policy is expressed as a stochastic perturbation of the actions or of the parameters of an underlying deterministic policy, we additionally establish global last-iterate convergence guarantees of C-PG to the optimal deterministic policy. This holds when learning a stochastic (hyper)policy and subsequently switching off the stochasticity at the end of training, thereby deploying a deterministic policy. Finally, we empirically validate both the action-based (C-PGAE) and parameter-based (C-PGPE) variants of C-PG on constrained control tasks, and compare them against state-of-the-art baselines, demonstrating their effectiveness, in particular when deploying deterministic policies after training.

Catoni-Style Change Point Detection for Regret Minimization in Non-Stationary Heavy-Tailed Bandits

Regret minimization in stochastic non-stationary bandits gained popularity over the last decade, as it can model a broad class of real-world problems, from advertising to recommendation systems. Existing literature relies on various assumptions about the reward-generating process, such as Bernoulli or subgaussian rewards. However, in settings such as finance and telecommunications, heavy-tailed distributions naturally arise. In this work, we tackle the heavy-tailed piecewise-stationary bandit problem. Heavy-tailed bandits, introduced by Bubeck et al., 2013, operate on the minimal assumption that the finite absolute centered moments of maximum order $1+\epsilon$ are uniformly bounded by a constant $v<+\infty$, for some $\epsilon \in (0,1]$. We focus on the most popular non-stationary bandit setting, i.e., the piecewise-stationary setting, in which the mean of reward-generating distributions may change at unknown time steps. We provide a novel Catoni-style change-point detection strategy tailored for heavy-tailed distributions that relies on recent advancements in the theory of sequential estimation, which is of independent interest. We introduce Robust-CPD-UCB, which combines this change-point detection strategy with optimistic algorithms for bandits, providing its regret upper bound and an impossibility result on the minimum attainable regret for any policy. Finally, we validate our approach through numerical experiments on synthetic and real-world datasets.

Thompson Sampling-like Algorithms for Stochastic Rising Bandits

Stochastic rising rested bandit (SRRB) is a setting where the arms' expected rewards increase as they are pulled. It models scenarios in which the performances of the different options grow as an effect of an underlying learning process (e.g., online model selection). Even if the bandit literature provides specifically crafted algorithms based on upper-confidence bounds for such a setting, no study about Thompson sampling TS-like algorithms has been performed so far. The strong regularity of the expected rewards in the SRRB setting suggests that specific instances may be tackled effectively using adapted and sliding-window TS approaches. This work provides novel regret analyses for such algorithms in SRRBs, highlighting the challenges and providing new technical tools of independent interest. Our results allow us to identify under which assumptions TS-like algorithms succeed in achieving sublinear regret and which properties of the environment govern the complexity of the regret minimization problem when approached with TS. Furthermore, we provide a regret lower bound based on a complexity index we introduce. Finally, we conduct numerical simulations comparing TS-like algorithms with state-of-the-art approaches for SRRBs in synthetic and real-world settings.

A Refined Analysis of UCBVI

In this work, we provide a refined analysis of the UCBVI algorithm (Azar et al., 2017), improving both the bonus terms and the regret analysis. Additionally, we compare our version of UCBVI with both its original version and the state-of-the-art MVP algorithm. Our empirical validation demonstrates that improving the multiplicative constants in the bounds has significant positive effects on the empirical performance of the algorithms.

Achieving $\widetilde{\mathcal{O}}(\sqrt{T})$ Regret in Average-Reward POMDPs with Known Observation Models

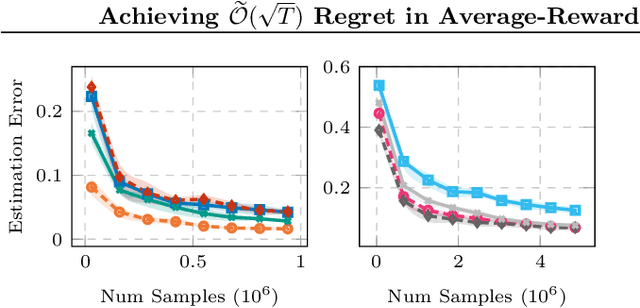
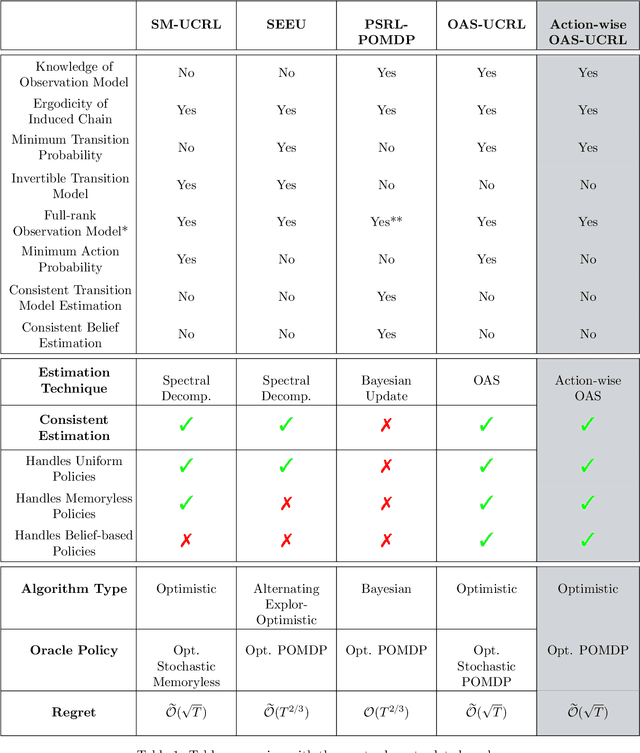
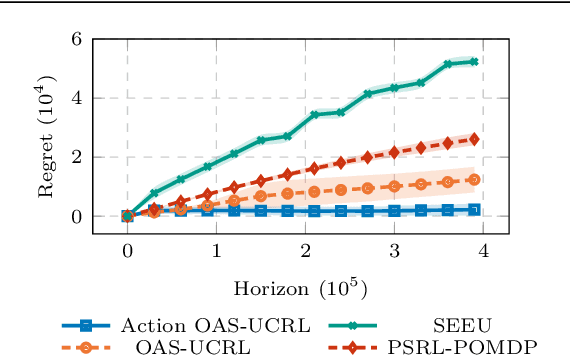
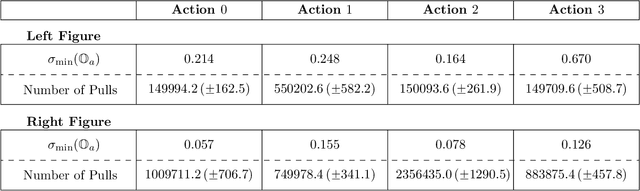
We tackle average-reward infinite-horizon POMDPs with an unknown transition model but a known observation model, a setting that has been previously addressed in two limiting ways: (i) frequentist methods relying on suboptimal stochastic policies having a minimum probability of choosing each action, and (ii) Bayesian approaches employing the optimal policy class but requiring strong assumptions about the consistency of employed estimators. Our work removes these limitations by proving convenient estimation guarantees for the transition model and introducing an optimistic algorithm that leverages the optimal class of deterministic belief-based policies. We introduce modifications to existing estimation techniques providing theoretical guarantees separately for each estimated action transition matrix. Unlike existing estimation methods that are unable to use samples from different policies, we present a novel and simple estimator that overcomes this barrier. This new data-efficient technique, combined with the proposed \emph{Action-wise OAS-UCRL} algorithm and a tighter theoretical analysis, leads to the first approach enjoying a regret guarantee of order $\mathcal{O}(\sqrt{T \,\log T})$ when compared against the optimal policy, thus improving over state of the art techniques. Finally, theoretical results are validated through numerical simulations showing the efficacy of our method against baseline methods.

On the Partial Identifiability in Reward Learning: Choosing the Best Reward

In Reward Learning (ReL), we are given feedback on an unknown *target reward*, and the goal is to use this information to find it. When the feedback is not informative enough, the target reward is only *partially identifiable*, i.e., there exists a set of rewards (the feasible set) that are equally-compatible with the feedback. In this paper, we show that there exists a choice of reward, non-necessarily contained in the feasible set that, *depending on the ReL application*, improves the performance w.r.t. selecting the reward arbitrarily among the feasible ones. To this aim, we introduce a new *quantitative framework* to analyze ReL problems in a simple yet expressive way. We exemplify the framework in a *reward transfer* use case, for which we devise three provably-efficient ReL algorithms.

Statistical Analysis of Policy Space Compression Problem

Policy search methods are crucial in reinforcement learning, offering a framework to address continuous state-action and partially observable problems. However, the complexity of exploring vast policy spaces can lead to significant inefficiencies. Reducing the policy space through policy compression emerges as a powerful, reward-free approach to accelerate the learning process. This technique condenses the policy space into a smaller, representative set while maintaining most of the original effectiveness. Our research focuses on determining the necessary sample size to learn this compressed set accurately. We employ R\'enyi divergence to measure the similarity between true and estimated policy distributions, establishing error bounds for good approximations. To simplify the analysis, we employ the $l_1$ norm, determining sample size requirements for both model-based and model-free settings. Finally, we correlate the error bounds from the $l_1$ norm with those from R\'enyi divergence, distinguishing between policies near the vertices and those in the middle of the policy space, to determine the lower and upper bounds for the required sample sizes.

Rising Rested Bandits: Lower Bounds and Efficient Algorithms

This paper is in the field of stochastic Multi-Armed Bandits (MABs), i.e. those sequential selection techniques able to learn online using only the feedback given by the chosen option (a.k.a. $arm$). We study a particular case of the rested bandits in which the arms' expected reward is monotonically non-decreasing and concave. We study the inherent sample complexity of the regret minimization problem by deriving suitable regret lower bounds. Then, we design an algorithm for the rested case $\textit{R-ed-UCB}$, providing a regret bound depending on the properties of the instance and, under certain circumstances, of $\widetilde{\mathcal{O}}(T^{\frac{2}{3}})$. We empirically compare our algorithms with state-of-the-art methods for non-stationary MABs over several synthetically generated tasks and an online model selection problem for a real-world dataset

Local Linearity: the Key for No-regret Reinforcement Learning in Continuous MDPs

Achieving the no-regret property for Reinforcement Learning (RL) problems in continuous state and action-space environments is one of the major open problems in the field. Existing solutions either work under very specific assumptions or achieve bounds that are vacuous in some regimes. Furthermore, many structural assumptions are known to suffer from a provably unavoidable exponential dependence on the time horizon $H$ in the regret, which makes any possible solution unfeasible in practice. In this paper, we identify local linearity as the feature that makes Markov Decision Processes (MDPs) both learnable (sublinear regret) and feasible (regret that is polynomial in $H$). We define a novel MDP representation class, namely Locally Linearizable MDPs, generalizing other representation classes like Linear MDPs and MDPS with low inherent Belmman error. Then, i) we introduce Cinderella, a no-regret algorithm for this general representation class, and ii) we show that all known learnable and feasible MDP families are representable in this class. We first show that all known feasible MDPs belong to a family that we call Mildly Smooth MDPs. Then, we show how any mildly smooth MDP can be represented as a Locally Linearizable MDP by an appropriate choice of representation. This way, Cinderella is shown to achieve state-of-the-art regret bounds for all previously known (and some new) continuous MDPs for which RL is learnable and feasible.