Approximate Equivariance in Reinforcement Learning

Equivariant neural networks have shown great success in reinforcement learning, improving sample efficiency and generalization when there is symmetry in the task. However, in many problems, only approximate symmetry is present, which makes imposing exact symmetry inappropriate. Recently, approximately equivariant networks have been proposed for supervised classification and modeling physical systems. In this work, we develop approximately equivariant algorithms in reinforcement learning (RL). We define approximately equivariant MDPs and theoretically characterize the effect of approximate equivariance on the optimal Q function. We propose novel RL architectures using relaxed group convolutions and experiment on several continuous control domains and stock trading with real financial data. Our results demonstrate that approximate equivariance matches prior work when exact symmetries are present, and outperforms them when domains exhibit approximate symmetry. As an added byproduct of these techniques, we observe increased robustness to noise at test time.

Partially Observable Contextual Bandits with Linear Payoffs

The standard contextual bandit framework assumes fully observable and actionable contexts. In this work, we consider a new bandit setting with partially observable, correlated contexts and linear payoffs, motivated by the applications in finance where decision making is based on market information that typically displays temporal correlation and is not fully observed. We make the following contributions marrying ideas from statistical signal processing with bandits: (i) We propose an algorithmic pipeline named EMKF-Bandit, which integrates system identification, filtering, and classic contextual bandit algorithms into an iterative method alternating between latent parameter estimation and decision making. (ii) We analyze EMKF-Bandit when we select Thompson sampling as the bandit algorithm and show that it incurs a sub-linear regret under conditions on filtering. (iii) We conduct numerical simulations that demonstrate the benefits and practical applicability of the proposed pipeline.

Near-Optimal Fair Resource Allocation for Strategic Agents without Money: A Data-Driven Approach

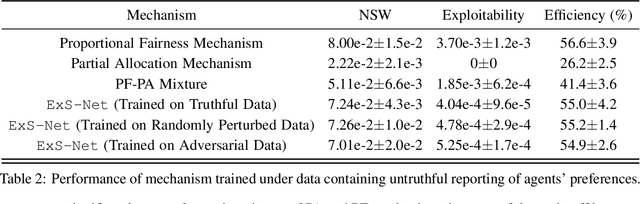
We study learning-based design of fair allocation mechanisms for divisible resources, using proportional fairness (PF) as a benchmark. The learning setting is a significant departure from the classic mechanism design literature, in that, we need to learn fair mechanisms solely from data. In particular, we consider the challenging problem of learning one-shot allocation mechanisms -- without the use of money -- that incentivize strategic agents to be truthful when reporting their valuations. It is well-known that the mechanism that directly seeks to optimize PF is not incentive compatible, meaning that the agents can potentially misreport their preferences to gain increased allocations. We introduce the notion of "exploitability" of a mechanism to measure the relative gain in utility from misreport, and make the following important contributions in the paper: (i) Using sophisticated techniques inspired by differentiable convex programming literature, we design a numerically efficient approach for computing the exploitability of the PF mechanism. This novel contribution enables us to quantify the gap that needs to be bridged to approximate PF via incentive compatible mechanisms. (ii) Next, we modify the PF mechanism to introduce a trade-off between fairness and exploitability. By properly controlling this trade-off using data, we show that our proposed mechanism, ExPF-Net, provides a strong approximation to the PF mechanism while maintaining low exploitability. This mechanism, however, comes with a high computational cost. (iii) To address the computational challenges, we propose another mechanism ExS-Net, which is end-to-end parameterized by a neural network. ExS-Net enjoys similar (slightly inferior) performance and significantly accelerated training and inference time performance. (iv) Extensive numerical simulations demonstrate the robustness and efficacy of the proposed mechanisms.

Oracle-free Reinforcement Learning in Mean-Field Games along a Single Sample Path

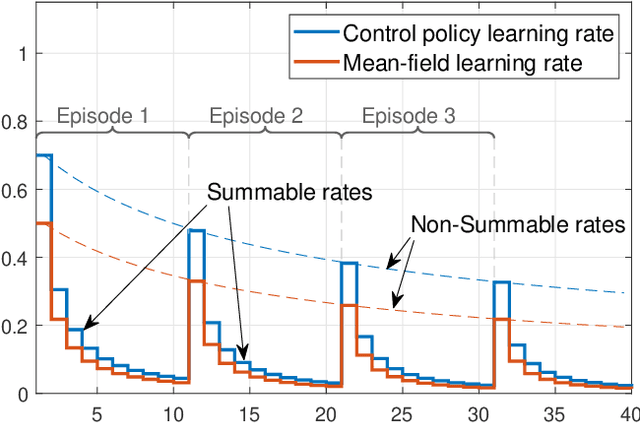
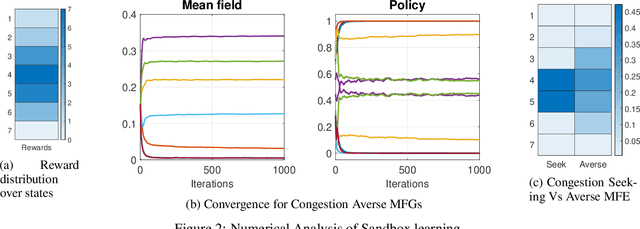
We consider online reinforcement learning in Mean-Field Games. In contrast to the existing works, we alleviate the need for a mean-field oracle by developing an algorithm that estimates the mean-field and the optimal policy using a single sample path of the generic agent. We call this Sandbox Learning, as it can be used as a warm-start for any agent operating in a multi-agent non-cooperative setting. We adopt a two timescale approach in which an online fixed-point recursion for the mean-field operates on a slower timescale and in tandem with a control policy update on a faster timescale for the generic agent. Under a sufficient exploration condition, we provide finite sample convergence guarantees in terms of convergence of the mean-field and control policy to the mean-field equilibrium. The sample complexity of the Sandbox learning algorithm is $\mathcal{O}(\epsilon^{-4})$. Finally, we empirically demonstrate effectiveness of the sandbox learning algorithm in a congestion game.

Catoni-style Confidence Sequences under Infinite Variance

In this paper, we provide an extension of confidence sequences for settings where the variance of the data-generating distribution does not exist or is infinite. Confidence sequences furnish confidence intervals that are valid at arbitrary data-dependent stopping times, naturally having a wide range of applications. We first establish a lower bound for the width of the Catoni-style confidence sequences for the finite variance case to highlight the looseness of the existing results. Next, we derive tight Catoni-style confidence sequences for data distributions having a relaxed bounded~$p^{th}-$moment, where~$p \in (1,2]$, and strengthen the results for the finite variance case of~$p =2$. The derived results are shown to better than confidence sequences obtained using Dubins-Savage inequality.

Extreme Bandits using Robust Statistics

We consider a multi-armed bandit problem motivated by situations where only the extreme values, as opposed to expected values in the classical bandit setting, are of interest. We propose distribution free algorithms using robust statistics and characterize the statistical properties. We show that the provided algorithms achieve vanishing extremal regret under weaker conditions than existing algorithms. Performance of the algorithms is demonstrated for the finite-sample setting using numerical experiments. The results show superior performance of the proposed algorithms compared to the well known algorithms.

Policy Gradient using Weak Derivatives for Reinforcement Learning

This paper considers policy search in continuous state-action reinforcement learning problems. Typically, one computes search directions using a classic expression for the policy gradient called the Policy Gradient Theorem, which decomposes the gradient of the value function into two factors: the score function and the Q-function. This paper presents four results:(i) an alternative policy gradient theorem using weak (measure-valued) derivatives instead of score-function is established; (ii) the stochastic gradient estimates thus derived are shown to be unbiased and to yield algorithms that converge almost surely to stationary points of the non-convex value function of the reinforcement learning problem; (iii) the sample complexity of the algorithm is derived and is shown to be $O(1/\sqrt(k))$; (iv) finally, the expected variance of the gradient estimates obtained using weak derivatives is shown to be lower than those obtained using the popular score-function approach. Experiments on OpenAI gym pendulum environment show superior performance of the proposed algorithm.